In the file, "PRE-AFTER JOIN-MEET ALGEBRAS", we postulated some results.

WE ESTABLISH P/A-JOIN AND P/A-MEET ALGEBRAS, with 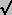, , 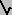, , 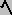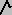as binary operators on integers:

• PREMEET ALGEBRA (BJ): a 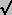b º lub{x| a Ù b = a Ù x};
• PREJOIN ALGEBRA (AR): a 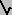b º glb{x| a Ú b = a Ú x};
• POSTMEET ALGEBRA (BR): a 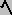b º lub{x| a Ù b = b Ù x};
• POSTJOIN ALGEBRA (AJ): a 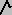b º glb{x| a Ú b = b Ú x}.

We now derive many consequences from these J-R Algebras.

---

META-OPERATORS (OPERATORS ON OPERATORS or ALGEBRAS)

The following shows that P/A Join-Meet Algebra is an algebra of algebras.

DUALITY º d: Ù → Ú. d(PM) = AM, d(AM) = PM, d(PJ) = AJ, d(AJ) = AJ.

TRANSPOSITION º t: t(PM) = PJ, t(PJ) = PM, t(AJ) = AM, t(AM) = AJ.

INVERSION º s = dt = td.

IDENTITY º i = dd = tt = vv.

This can be graphed (with consequences noted in a file to follow):

			PM<--d--->PJ
                          ^ \   /^
                          | s\ / |
                         t|   \  |t
                          |  / \ |
                          | /s  \|
                          V      V
                        AM<--d--->AJ

A consequence is:

JOIN-MEET CAYLEY-TABLE

	d	t	s	i
d	i	s	t	d
t	s	i	d	t
s	t	d	i	s
i	d	t	s	i

---

HEY! That's the TABLE OF THE VIERGRUPPE (FOURGROUP). Then: P/A JOIN-MEET ALGEBRA IS THE STUDY OF ORDINOLOGICAL PROPERTIES CONSERVED UNDER THE VIERGRUPPE! What are these?

---

POSET THEOREM: Any system satsifying ALL the conditions of PRE/AFTER JOIN-MEET ALGEBRAS is a POSET (partially ordered set).

PROOF: In the PRE-algebras, for any element a, set x = b; and in the POST-algebras, for any element b, set x = a.

LATTICE THEOREM: Any system uniquely satsifying the conditions of PRE/AFTER JOIN-MEET ALGEBRAS is a LATTICE. (Proof: Obvious.)

Thus, these algebras are "roots of poset and lattice algebras". Assignment: Does exploring this relation reveal anything new?