SCHÖNHEIT UND BAUCH-TASTEN

RÄTSEL: Was macht ein QUADRAT, einen KREIS, und hat DAS GOLDENE MITTEL (oder GOLDENER ABSCHNITT, oder GOLDENES VERHÄLTNIS, oder GÖTTLICHES VERHÄLTNIS) gemeinsam? (Sie können einen Graduierten Mathestudenten für Hilfe auf dies fragen).

ANTWORT: Sie benutzen UNVERNÜNFTIGE ZAHLEN für IDEAL oder MAXIMIN ( "am meisten für wenigst") REALISIERUNG der SCHÖNHEIT.

Ich werde erklären. (Und Bauchnabel werden herausspringen).

HÖREN Sie JETZT DIES!! Alle drei von diesen erreichen MAXIMIN SCHÖNHEIT über UNVERNÜNFTIG METRISCH:
  1. DIE DIAGONALE VON EINEM QUADRAT BEZIEHT SICH AUF DAS QUADRAT ALS DER DURCHMESSER VON EINEM KREIS ZUM KREIS. DIE DIAGONALE VON EINEM QUADRAT IST UNMESSBAR MIT SEINEN SEITEN (IM VERHÄLTNIS, für irgendeine Seite von Länge S: (2)S/S = 2.
  2. DAS VERHÄLTNIS VOM DURCHMESSER VON EINEM KREIS ZU SEINEM UMFANG IST DIE UNVERNÜNFTIGE ZAHL .

    GEGEBEN EIN ABSCHNITT VON LÄNGE 1 + x, HABEN WIR DAS VERHÄLTNIS: 1/x = x/(1 + x). (Der PUNKT, der SUBSEGMENT 1 VON SUBSEGMENT x TEILT, ist DER GOLDENE MITTELpunkt: "B".)

    Lassen Sie x = , das NORMALE SYMBOL für das GOLDENE MITTEL. Dann wird das VERHÄLTNIS , führend zur Gleichung: 1/ = /(1 + ). Dies hat das (positive Lösung) 1/2(1 ± (1 + 4)1/2) = 1/2(1 + (5)1/2) = 1.618033988749894848204586834365638117720. . .. Deutlich ein irrattional (transzendent) Zahl!

    Eigentlich rufen einige Mathematiker diese Zahl, , "Die unvernünftigste Zahl"! Warum? Weil Sie können schreiben VERNÜNFTIGE und UNVERNÜNFTIGE ZAHLEN als "Bruchteile" fortgesetzt hat, mit Zähler von 1. Eine VERNÜNFTIGE ZAHL, wenn geschrieben, während ein fortgesetzter Bruchteil BEENDIGT, aber eine UNVERNÜNFTIGE ZAHL NICHT BEENDIGT!

    Beispiel: 5/7 = 1/(7/5) = 1/(1 + 2/5) = 1/(1 + 1/(5/2)) = 1/(1 + 1/(2 + 1/2)) -- BEENDIGT.

    Aber =

         1   
    1 + 1   
       1 + 1   
          1 + 1     
             1 + 1   
                1 + ....
    Bedeutung, die der Untergeordnete Bruchteile mit Zähler 1 EWIG WEITERGEHT!

    Merkt, daß Sie ihm zu 1/(1/1) = 1 annähern können; oder 1/(1/1 + 1) = 1/(1/2) = 2; oder 1/((1 + 1/(1 + 1)) = 3/2; usw. Diese sind Ruf seiner zusammenlaufenden: 1, 2, 3/2, 5/3, 8/5, ..... Aber diese sind DIE VERHÄLTNISSE VON FORTLAUFENDEN FIBONACCI ZAHLEN!

    In der acompanying CHRONOLOGIE Akte ist Mathematiker Fibonacci für Herausgeben (IN 1202) das ERSTE europäische BUCH erwähnt, das DEZIMALaufzählung BENUTZT, römische ZIFFERN ZU ERSETZEN. In seinem Buch hat Fibonacci ein "Wortproblem" um die Reproduktion der Hasen aufgestellt.

    Fangen Sie mit 1 und 1 an. Fügen Sie diese hinzu, um 2 zu erhalten. Fügen Sie die zweiten 1 und 2, für 323, für 5 hinzu. 3 + 5 = 8. 5 + 8 = 13. Usw.

    FIBONACCI REIHENFOLGE: 1, 1, 2, 3, 5, 8, 13, 21, 34,.... (Ein bewegend Zwei-summieren).

    So was? BIOLOGEN HABEN ENTDECKT, daß DIES IST DAS NUMERISCHE GEHEIMNIS VON PHYLLOTAXIS -- DEM WEG SCHNECKENWINDUNG UM EINEN PFLANZE STAMM (in FIBONACCI VERHÄLTNISSEN: (3, 5, 8, 13, 21, 34, 85). Oder Schneckenwindung, als im Gänseblümchen. DAISYFolglich, "Gott benutzt DAS GOLDENE MITTEL, BLUMEN UND ANDERE PFLANZEN UND TIERE ZU ENTWERFEN!."

    Alte Griechische haben gesagt, daß EINE GESTALTE FRAU DIE GOLDENEN MITTELverhältnisse GEHABT HAT. Was bedeutet der?

    Erinnern Sie sich an: Und VERHÄLTNIS: 1/x = x/(1 + x).

    Lassen Sie 01 vertreten DIE ENTFERNUNG VOM OBERTEIL VOM KOPF EINER GESTALTER FRAU ZU IHREM BAUCHNABEL; läßt x vertreten DIE ENTFERNUNG VON IHREM BAUCHNABEL ZU DEN SOHLEN VON IHREN FÜSSEN. DANN IST IHRE HÖHE 1 + x , deshalb hat sie die VERHÄLTNISSE VOM GOLDENEN MITTEL. IHR BAUCHNABEL ist DER GOLDENE MITTELpunkt. (Siehe. Ich habe Ihnen das erzählt "Bauchnabel werden herausspringen"!)

    Sandro Botticelli (1445-1510) hat die Verhältnisse beim Zug der Figur von Venus beim Der Gemäldes imaged oben benutzt. Wir kennen dieses weil, in seinem Buch, Den Kurven dem Leben (1979), Theodore Koch hat unterteilt die Venus Figur im Botticelli Gemälde. Kochen Sie hat gemessen das VERHÄLTNIS: (-zu-Oberteil-Kopf)/(Zentrum=zu-Füßen) = / 4 + 5) = 5)/6 = 1/ d.h. 1: f, damit ihre Länge ost 1 + f, das GOLDENES MITTEL (DEVINE) VERHÄLTNIS! .

    You've also seen this proportion when you've drawn the five-point star. Each intersection of a segment by another segment in it divides the intersected segment in the golden proportion.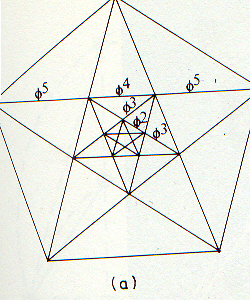
    WAS IST DER PUNKT VON ALLEN DIES?

    "Um am meisten für das wenigste zu werden", BENUTZEN GOTT und Künstler und Ingenieure UNVERNÜNFTIGE ZAHLEN!! EINE UNVERNÜNFTIGE ZAHL WÄHLT EINEN SCHÖNHEIT PUNKT ODER EINEN SCHÖNHEIT ABSCHNITT ODER EINE SCHÖNHEIT OBERFLÄCHE AUS.

    Für, ist ein anderes Beispiel für die Schönheit von Natur eine Seifenblase: eine OBERFLÄCHE MINIMALER KRÜMMUNG, die von Seifenfilm gebildet wird. Die einfachste Blase ist eine einzelne SPHÄRE, die -- wie der KREIS -- als ein MEHRFACHES vom unvernünftigen (transzendent) Zahl gebaut ist. Kompliziertere Formen finden statt, wenn 0mehrfache Blasen zusammen angeschlossen sind.

    Zwei hervorragende Blasenprobleme:

    1. Um die Anordnungen mit dem kleinsten Umfang (planar Problem) zu finden
    2. Oder die kleinste Fläche (Gebietproblem)

    Welcher einschließt, und trennt n Gegeben Einheitengebiete oder Bände in der Ebene oder in Platz. Für n = 2, Sind die Probleme gerufen das "Verdoppelt Blasenvermutung" und die Lösung beide zum planar Problem und das Gebiet Problem ist gekannt, das zu sein Doppelte Blase

.

Auch ist die Doppelte Blase gekannt, zu sein Gebietminimieren ("Most-least"). Aber es ist weiß nicht noch, wenn die Dreifache Blase ist Gebietminimieren.

Blasenforschung wurde vom Belgischen Physiker, Joseph Plateau (1801-1886). Und viele verwandte Probleme sind noch ungelöst -- "Schönheit unerforschlich".

Haben Sie Regenbogen auf der Oberfläche von Seifenblasen bemerkt? Das zeigt Sie der das Regenbogen Auch wird von "unvernünftigem Mittel" gebaut.

Wiederholung, "Um am meisten für das wenigste zu werden", BENUTZEN GOTT und Künstler und Ingenieure UNVERNÜNFTIG (TRANSZENDENT) ZAHLEN!!

Alle dies, und MEHR, ist DAS QUADRATISCHE TOR durchgekommen.