BEAUTÉ ET VENTRE-BOUTONS DE FEMMES

ÉNIGME: Que est-ce qu'une PLACE, un CERCLE, et LE MOYEN D'OR (également connu sous le nom de SECTION D'OR, ou RAPPORT D'OR, ou PROPORTION DIVINE) ont en commun? (Vous pouvez demander à un étudiant gradué de maths l'aide sur ceci.)

RÉPONSE: Ils emploient TRANSCENDENT OU NOMBRES IRRATIONNELS pour RÉALISATION OPTIMALE ou de MAXIMIN ("la plus pour mineurs") de la BEAUTÉ.

J'expliquerai cela. (Et les ventre-boutons sauteront dehors.)

  1. Une PLACE EST CE POLYGONE QUI RÉALISE Le SECTEUR MAXIMUM AVEC La FRONTIÈRE MINIMUM (APPELÉE "PÉRIMÈTRE", COMPARABLES À la "CIRCONFÉRENCE D'un CERCLE") -- RÉALISATION De la BEAUTÉ De MAXIMIN.
  2. Un CERCLE EST CETTE FIGURE PLATE QUI RÉALISE Le SECTEUR MAXIMUM AVEC La FRONTIÈRE MINIMUM (APPELÉE "CIRCONFÉRENCE", COMPARABLES Au "PÉRIMÈTRE" D'un POLYGONE) -- RÉALISATION De la BEAUTÉ De MAXIMIN.
  3. LE MOYEN D'OR EST CETTE DIVISION (FRONTIÈRE) DU SEGMENT DE LIGNE QUI FORMS LA PLUS GRANDE CORRÉLATION PAR LA MOINDRE PROLONGATION -- RÉALISATION DE LA BEAUTÉ DE MAXIMIN.

ATTENTION!!! Chacun des trois de ces RÉALISATIONS réalise la BEAUTÉ de MAXIMIN par l'intermédiaire de la MÉTRIQUE IRRATIONNELLE de TRANSCENDENT:

  1. La DIAGONALE D'une PLACE SE RELIE À la PLACE COMME DIAMÈTRE D'un CERCLE Au CERCLE.
  2. LA DIAGONALE D'une PLACE EST INCOMMENSURABLE AVEC SES CÔTÉS (DANS LE RAPPORT, pour tout côté de longueur S: 21/2S/S = 21/2.
  3. LE RAPPORT DU DIAMÈTRE D'un CERCLE à SA CIRCONFÉRENCE EST LE TRANSCENDENT OU LE NOMBRE IRRATIONNEL
  4. DONNÉ Un SEGMENT DE LA LONGUEUR, 1 + x, NOUS AVONS LE RAPPORT: 1/x = x/(1 + x). (Le POINT DIVISANT LE SOUS-SEGMENT 1 DU SOUS-SEGMENT x est LE POINT MOYEN D'OR: "B".) .
Laissez x = , le SYMBOLE STANDARD pour le MOYEN D'OR. Alors le RAPPORT devient 1/ = /(1 + , menant à l'équation: 2 - + 1 = 0. Ceci a (solution positive) le 1/2(1 ± (1 + 4)1/2) = 1/2(1 + (5)1/2) = 1.618033988749894848204586834365638117720. . ., clairement, un TRANSCENDENT OU un NOMBRE IRRATIONNEL!

En fait, quelques mathématiciens demandent ce numéro, , "le nombre le plus irrationnel"! Pourquoi? Puisque vous pouvez écrire des NOMBRES RAISONNABLES et IRRATIONNELS en tant que "fractions continues", avec le DÉNOMINATEUR de 1. Un NOMBRE RAISONNABLE, une fois écrit comme fraction continue SE TERMINE, mais un NOMBRE IRRATIONNEL NE SE TERMINE PAS SOUS LA FORME CONTINUE de FRACTION!

Exemple: 5/7 = 1/(7/5) = 1/(1 + 2/5) = 1/(1 + 1/(5/2)) = 1/(1 + 1/(2 + 1/2)) -- TERMINE le

Mais le = 

     1   
    1 + 1   
       1 + 1   
          1 + 1     
             1 + 1   
                1 + ....
Meaning que les subfractions avec le numérateur 1 CONTINUENT POUR TOUJOURS!

Notez que vous pouvez l'approcher de 1/(1/1) = 1; ou 1/(1/1 + 1) = 1/(1/2) = 2; ou 1/((1 + 1/(1 + 1)) = 3/2; etc... Ce sont appel son convergents: 1, 2, 3/2, 5/3, 8/5..... Mais ce sont LES RAPPORTS DES NOMBRES CONSÉCUTIFS de FIBONACCI!

Dans le dossier acompanying de CHRONOLOGIE, mathématicien Fibonacci est mentionné pour éditer (EN 1202) le PREMIER LIVRE EUROPÉEN EN UTILISANT LA NUMÉRATION DÉCIMALE POUR REMPLACER LES NUMÉROS ROMAINS. En son livre, Fibonacci a posé un "problème de mot" au sujet de la reproduction des lapins.

Les BIOLOGISTES ONT DÉCOUVERT que est le "SECRET" NUMÉRIQUE DE PHYLLOTAXIS -- La MANIÈRE PLANTE SPIRALE AUTOUR D'une TIGE D'cusine (dans des RAPPORTS de FIBONACCI: 1/2, 1/3, 2/5, 3/8, 5, 13, etc.). LE NOMBRE DE PÉTALES EN QUELQUES FLEURS (3, 5, 8, 13, 21, 34, 85). Ou spirale, comme dans la marguerite, DAISY. Ainsi, "Dieu emploie LE MOYEN D'OR DE CONCEVOIR DES FLEURS ET d'cAutres USINES ET ANIMAUX!"

Les artistes ont employé LE MOYEN D'OR depuis la GRÈCE ANTIQUE: DANS LE PARTHENON; EN statue de VENUS DE MILO de PRAXITELES'; DANS LES PROPORTIONS DE PEINTURES de la RENAISSANCE, telles que naissance de Botticelli la "de Venus". Etc...

l'architecte français Le Corbusier a employé le RECTANGLE D'OR en concevant WINDOWS de ses BÂTIMENTS, .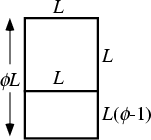

Les Grecs antiques ont dit qu'Une FEMME BIEN FAITE A EU LES PROPORTIONS MOYENNES D'OR. Que ce moyen?

Rappelez-vous: Et RAPPORT: 1/x = x/(1 + x).

Laissez 1 représenter LA DISTANCE DU DESSUS DE LA TÊTE D'une FEMME BIEN FAITE à SON Ventre-bouton; laissez x représenter LA DISTANCE de SON Ventre-bouton AUX SEMELLES de SES PIEDS. ALORS SA TAILLE EST 1 + x, ainsi elle a les PROPORTIONS DU MOYEN D'OR. SON Ventre-bouton est LE POINT MOYEN D'OR. (Voyez que je vous ai dit que les "ventre-boutons sauteront hors de"!)

Sandro Botticelli (1445-1510) a employé ces proportions en dessinant la figure de Venus dans ce qui précède reflètent de peinture. Nous savons ceci parce que, en son livre, Les Courbes de vie (1979), Theodore cool ont subdivisé le chiffre de Venus dans la peinture de Botticelli. Cook a mesuré le RAPPORT: (nombril jusqu au dessus de la tête)/(nombril aux pieds) = 5 /(5) = 5 /, au 1:, de sorte que sa longueur is 1 + , la PROPORTION (DEVINE) MOYENNE D'OR!

Vous avez également vu cette proportion quand vous avez dessiné d'étoile de cinq-point. Chaque intersection d'un segment par un autre segment dans elle divise le segment intersecté dans la proportion d'or. pour, un autre exemple de la beauté de la nature est une bulle de savon: une SURFACE DE LA COURBURE MINIMALE a formé par le film de savon. La bulle la plus simple est une SPHÈRE simple, que -- comme le CERCLE -- est construit comme MULTIPLE du nombre irrationnel, Des formes plus compliquées se produisent quand des bulles multiples sont jointes ensemble.

Deux problèmes en suspens de "bulle":

  1. pour trouver les arrangements avec le plus petit périmètre (problème planaire)
  2. la superficie -- ou plus petite (problème de secteur)
. Qui joint et sépare des unités de superficie ou des volumes indiqués par n dans l'avion ou dans l'espace. Pour n = 2, les problèmes s'appellent la "double conjecture de bulle" et la solution au problème planaire et au problème de secteur est connue pour être la double bulle. En outre, la double bulle est connue secteur-réduire au minimum ("plus-moindre"). Mais elle ne doit pas encore savoir si la bulle triple secteur-réduit au minimum.

La recherche de bulle a été lancée par le physicien belge, Joseph Plateau (1801-1886). Et beaucoup de problèmes relatifs sont encore non résolus -- "beauté impénétrable".

Avez-vous noté des "arcs-en-ciel" sur la surface des bulles de savon? Ce expositions vous que l'arc-en-ciel est également construit par "des moyens irrationnels".

Répétant, "pour obtenir les la plupart pour UTILISATION TRANSCENDENT OU NOMBRES IRRATIONNELS moins", d'un DIEU et d'artistes et d'ingénieurs!!!

Tout ceci, et PLUS, sont venus par LA PORTCARRÉ.