ANSWER: They use IRRATIONAL NUMBERS for OPTIMAL or MAXIMIN ("mostest for leestest") REALIZATION of BEAUTY.
Dig? OK, I'll redig that one. (And belly-buttons will pop out.)
- A SQUARE IS THAT POLYGON WHICH ACHIEVES MAXIMUM AREA WITH MINIMUM BOUNDARY (CALLED "PERIMETER", COMPARABLE TO THE "CIRCUMFERENCE OF A CIRCLE") -- ACHIEVING MAXIMIN BEAUTY.
- A CIRCLE IS THAT PLANE FIGURE WHICH ACHIEVES MAXIMUM AREA WITH MINIMUM BOUNDARY (CALLED "CIRCUMFERENCE", COMPARABLE TO THE "PERIMETER" OF A POLYGON) -- ACHIEVING MAXIMIN BEAUTY.
- THE GOLDEN MEAN IS THAT DIVISION (BOUNDARY) OF LINE SEGMENT WHICH FORMS THE GREATEST INTERRELATIONSHIP BY THE LEAST EXTENSION -- ACHIEVING MAXIMIN BEAUTY
NOW HEAR THIS!!! All three of these achieve MAXIMIN BEAUTY via IRRATIONAL METRICS:
- THE DIAGONAL OF A SQUARE RELATES TO THE SQUARE AS THE DIAMETER OF A CIRCLE TO THE CIRCLE. THE DIAGONAL OF A SQUARE IS INCOMMENSURABLE WITH ITS SIDES (IN THE RATIO, for any side of length S: (2)1/2S/S = (2)1/2).
- THE RATIO OF THE DIAMETER OF A CIRCLE TO ITS CIRCUMFERENCE IS THE IRRATIONAL NUMBER p.
- GIVEN A SEGMENT OF LENGTH 1 + x, WE HAVE THE RATIO: 1/x = x/(1 + x). (The POINT DIVIDING SUBSEGMENT 1 FROM SUBSEGMENT x is THE GOLDEN MEAN POINT: "B".)

Let x = f, the STANDARD SYMBOL for the GOLDEN MEAN. Then the RATIO becomes 1/f = f/(1 + f), leading to the equation: f2 - f - 1 = 0. This has the (positive solution) 1/2(1 ± (1 + 4)1/2) = 1/2(1 + (5)1/2) = 1.618033988749894848204586834365638117720. . .. Clearly, an IRRATIONAL NUMBER!
In fact, some mathematicians call this number, f, "the most irrational number"! Why? Because you can write RATIONAL and IRRATIONAL NUMBERS as "continued fractions", with DENOMINATOR of 1. A RATIONAL NUMBER, when written as a contInued fraction TERMINATES, but an IRRATIONAL NUMBER DOES NOT!
Example: 5/7 = 1/(7/5) = 1/(1 + 2/5) = 1/(1 + 1/(5/2)) = 1/(1 + 1/(2 + 1/2)) -- TERMINATES.
But f =
1 1 + 1 1 + 1 1 + 1 1 + 1 1 + ....Meaning that the subfractions with numerator 1 GO ON FOREVER!Note that you can approximate it to 1/(1/1) = 1; or 1/(1/1 + 1) = 1/(1/2) = 2; or 1/((1 + 1/(1 + 1)) = 3/2; etc. These are call its convergents: 1, 2, 3/2, 5/3, 8/5, .... But these are THE RATIOS OF CONSECUTIVE FIBONACCI NUMBERS!
In the acompanying CHRONOLOGY file, mathematician Fibonacci is mentioned for publishing (IN 1202) the FIRST EUROPEAN BOOK USING DECIMAL NUMERATION TO REPLACE ROMAN NUMERALS. In his book, Fibonacci posed a "word problem" about the reproduction of rabbits.Start with 1 and 1. Add these to obtain 2. Add the second 1 and 2, for 3. Add the 2 and 3, for 5. 3 + 5 = 8. 5 + 8 = 13. Etc.
FIBONACCI SEQUENCE: 1, 1, 2, 3, 5, 8, 13, 21, 34, .... (A moving 2-sum).
So what? BIOLOGISTS DISCOVERED THIS IS THE NUMERICAL "SECRET" OF PHYLLOTAXIS -- THE WAY LEAVES SPIRAL AROUND A PLANT STEM (in FIBONACCI RATIOS: 1/2, 1/3, 2/5, 3/8, 5, 13, etc.). THE NUMBER OF PETALS IN SOME FLOWERS (3, 5, 8, 13, 21, 34, 85). Or spiral, as in the Daisy.
 Thus, "God uses THE GOLDEN MEAN TO DESIGN FLOWERS AND OTHER PLANTS AND ANIMALS!"
Thus, "God uses THE GOLDEN MEAN TO DESIGN FLOWERS AND OTHER PLANTS AND ANIMALS!"
Artists have used THE GOLDEN MEAN since ANCIENT GREECE: IN THE PARTHENON; IN PRAXITELES' VENUS DE MILO; IN PROPORTIONS OF RENAISSANCE PAINTINGS, such as Botticelli's "Birth of Venus". Etc.
Etc.The French architect Le Corbusier used the GOLDEN RECTANGLE
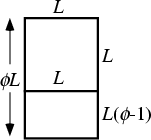 in designing WINDOWS of his BUILDINGS.
in designing WINDOWS of his BUILDINGS.Ancient Greeks said that A SHAPELY WOMAN HAD THE GOLDEN MEAN PROPORTIONS. What does that mean?
Remember:
 And RATIO: 1/x = x/(1 + x).
And RATIO: 1/x = x/(1 + x).Let 1 represent THE DISTANCE FROM THE TOP OF A SHAPELY WOMAN'S HEAD TO HER BELLY-BUTTON; let x represent THE DISTANCE FROM HER BELLY-BUTTON TO THE SOLES OF HER FEET. THEN HER HEIGHT IS 1 + x, so she has the PROPORTIONS OF THE GOLDEN MEAN. HER BELLY-BUTTON is THE GOLDEN MEAN POINT. (See. I told you that "belly-buttons will pop out"!)
Sandro Botticelli (1445-1510) used those proportions in drawing the figure of Venus in the painting imaged above. We know this because, in his book, The Curves of Life (1979), Theodore Cook subdivided the Venus figure in the Botticelli painting. Cook measured the RATIO: navel-to-top-of-head/navel-to-feet = f5/(f4 + f5) = f5/f6 = 1/f, that is, 1:f, so that her length is 1 + f, the GOLDEN MEAN (DEVINE) PROPORTION!
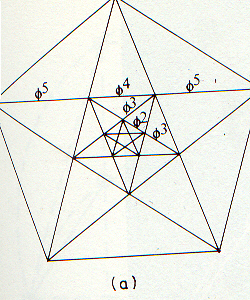
You've also seen this proportion when you've drawn the five-point star. Each intersection of a segment by another segment in it divides the intersected segment in the golden proportion.
WHAT'S THE POINT OF ALL THIS?"Tuh git thuh mostest fur thuh leestest", GOD and artists and engineers USE IRRATIONAL NUMBERS!!! AN IRRATIONAL NUMBER SELECTS A BEAUTY POINT OR A BEAUTY SEGMENT OR A BEAUTY SURFACE.
For, another example of Nature's beauty is a soap bubble: a SURFACE OF MINIMAL CURVATURE formed by soap film. The simplest bubble is a single SPHERE, which -- like the CIRCLE -- is constructed as a MULTIPLE of the irrational number, p. More complicated forms occur when multiple bubbles are joined together.
Two outstanding "bubble" problems:
- to find the arrangements with the smallest Perimeter (planar problem)
- or the smallest Surface Area (area problem)
which enclose and separate n given unit areas or volumes in the plane or in space. For n = 2, the problems are called the "Double Bubble Conjecture" and the solution both to the planar problem and the area problem is known to be the Double Bubble. Also, the Double Bubble is known to be area-minimizing ("mostest-leestest"). But it is not yet know if the Triple Bubble is area-minimizing.
Bubble research was initiated by the Belgian physicist, Joseph Plateau (1801-1886). And many related problems are still unsolved -- "beauty inscrutable".
Have you noticed "rainbows" on the surface of soap bubbles? That shows you that the rainbow is also constructed by "irrational means".
NATURAL MÖBOIDS IN SOAP FILM
(adapted from What Is Mathematics?, Richard Courant and Herbert Robbins, pp. 388-9)It has been observed that soap film "seeks" minimal surfaces, and (Belgian) Joseph Plateau (1801-83) has shown the mathematics of this.
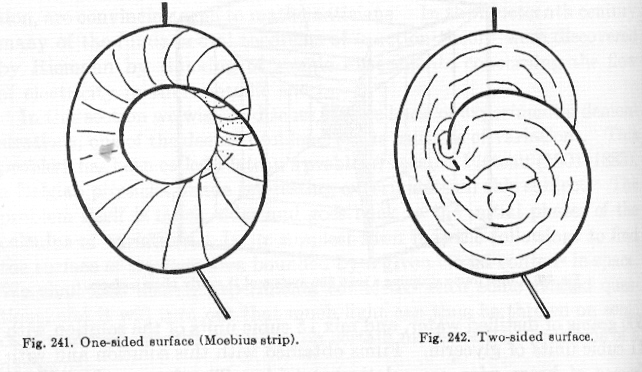
Let the wire frame be that of a disk (filled-in circle).
"If we continuously deform the boundary circle [outside circle of disk] we might expect that the minimal surface would also retain the topological character of disk. This is not the case. If the boundary is deformed into the shape indicated by Figure. 241 [below], we obtain a minimal surface that is no longer simply connected, like the disk, but a one-side Moebius strip. Conversely, we might start with this [wire] frame and with a soap film in the shape of a Moebius strip. We may deform the wire frame by pulling handles soldered to it (Fig. 241). In this process we shall reach a moment when suddenly the topological character of the film changes, so that the surface is again of the type of a simply connected disk (Fig. 142). Reversing the deformation we again obtain a Moebius strip. In this alternatig deformation process the mutation of the simply connected surface into the Moebius strip takes place at a later stage.
"This shows that there must be a range of shapes of the contour for which both the Moebius strip and the simply connected surface are stable, i.e. furnish relative minima. But when the Moebius strip has a much smaller area than the other [disk] surface, the latter [disk] is too unstable to be formed."
 Repeating, "Tuh git thuh mostest fur thuh leestest", GOD and artists and engineers USE IRRATIONAL NUMBERS!!!
Repeating, "Tuh git thuh mostest fur thuh leestest", GOD and artists and engineers USE IRRATIONAL NUMBERS!!!
All this, and MORE, came through THE SQUARE GATE.