RISPOSTA: Usano TRANCENDENT o i NUMERI IRRAZIONALI per REALIZZAZIONE di MAXIMIN o OTTIMALE ("più per minimi") del === che di BELLEZZA spiegherò. (ed i tasti della pancia schioccheranno fuori.),
- Un QUADRATO È QUEL POLIGONO CHE REALIZZA La ZONA MASSIMA CON Il CONTORNO MINIMO (CHIAMATO "PERIMETRO", PARAGONABILI "Alla CIRCONFERENZA Di un CERCHIO") -- REALIZZANDO La BELLEZZA Di MAXIMIN.
- Un CERCHIO È QUELLA FIGURA PIANA CHE REALIZZA La ZONA MASSIMA CON Il CONTORNO MINIMO (CHIAMATO" CIRCONFERENZA ", PARAGONABILI "Al PERIMETRO" Di un POLIGONO) -- REALIZZARE La BELLEZZA Di MAXIMIN.
- LA MEDIA DORATA È QUELLA DIVISIONE (CONTORNO) DEL SEGMENTO DI LINEA CHE FORMS LA CORRELAZIONE PIÙ GRANDE DALLA MENO ESTENSIONE -- REALIZZARE BELLEZZA DI MAXIMIN.
- La DIAGONALE Di un QUADRATO SI RIFERISCE Al QUADRATO COME Il DIAMETRO Di un CERCHIO Al
CERCHIO. LA DIAGONALE Di un QUADRATO È INCOMMENSURABLE CON i RELATIVI LATI (NEL RAPPORTO, per
qualsiasi lato della lunghezza
2S/S = 2).
- IL RAPPORTO DEL DIAMETRO Di un CERCHIO alla RELATIVA CIRCONFERENZA È IL NUMERO IRRAZIONALE
.
- DATO Un SEGMENTO DELLA LUNGHEZZA 1 + x, ABBIAMO IL RAPPORTO:
1/x = x/(1 + x). (Il PUNTO che DIVIDE IL SUBSEGMENT 1 DAL
SUBSEGMENT x è IL PUNTO MEDIO DORATO: "B". Il ha lasciato x =
, il SIMBOLO STANDARD per la MEDIA DORATA. Allora il
RAPPORTO diventa 1/ = /(1 + ), conducente all'equazione: 2 -
- 1 = 0. Ciò ha (soluzione positiva) il 1/2(1
±(1 + 4)1/2) = 1/2(1 + (5)1/2) =
1.618033988749894848204586834365638117720. . .. Chiaramente, un IRRAZIONALE
NUMBER!Infatti, alcuni matematici denominano questo numero,
, "il numero più
irrazionale"! Perchè? Poiché potete scrivere i NUMERI RAZIONALI ed IRRAZIONALI come "frazioni
continuate", con un NUMERATORE di 1. Un NUMERO RAZIONALE, una volta
scritto come frazione continuata TERMINA, ma un NUMERO IRRAZIONALE NON TERMINA!Esempio: 5/7 = 1/(7/5) = 1/(1 + 2/5) = 1/(1 + 1/(5/2)) = 1/(1 + 1/(2 + 1/2)) TERMINA.
Ma
=1 1 + 1 1 + 1 1 + 1 1 + 1 1 + ....Significando che i suddetti subfractions con il numeratore 1 ACCENDONO PER SEMPRE!Noti che potete avvicinarseli a 1/(1/1) = 1; o 1/(1/1 + 1) = 1/(1/2) = 2; o 1/((1 + 1/(1 + 1)) = 3/2; ecc. Queste sono chiamata le relative convergenze: 1, 2, 3/2, 5/3, 8/5.... Ma questi sono I RAPPORTI DEI NUMERI SUCCESSIVI del FIBONACCI!
Nella lima acompanying di CRONOLOGIA, il matematico Fibonacci è accennato per la pubblicazione (in 1202) del PRIMO LIBRO EUROPEO USANDO IL NUMERATION DECIMALE PER SOSTITUIRE I NUMERI ROMANI. In suo libro, Fibonacci ha proposto "un problema di parola" circa riproduzione dei conigli.Inizi con 1 e 1. Aggiunga questi per ottenere 2. Aggiunga il secondi 1 e 2 , per 3. Aggiunga i 2 ed i 3 , per 5. 3 + 5 = 8. 5 + 8 = 13. Ecc.
SEQUENZA DEL FIBONACCI: 1, 1, 2, 3, 5, 8, 13, 21, 34.... (2-somme commoventi di A).
Così che cosa? I BIOLOGHI HANNO SCOPERTO che QUESTO È "IL SEGRETO" NUMERICO DI PHYLLOTAXIS -- IL SENSO LASCIA LA SPIRALE INTORNO Ad un GAMBO della PIANTA (nei RAPPORTI del FIBONACCI: 1/2, 1/3, 2/5, 3/8, 5, 13, ecc.). IL NUMERO DI PETALI IN ALCUNI FIORI (3, 5, 8, 13, 21, 34, 85). O si sviluppa a spirale, come la margherita
. In usi del dio, così LA MEDIA DORATA
PROGETTARE I FIORI ED ALTRI PIANTE ED ANIMALI!"
Gli artisti hanno usato LA MEDIA DORATA dalla GRECIA ANTICA: NEL PARTHENON; IN VENUS DE MILO DEL PRAXITELES; NELLE PROPORZIONI DELLE PITTURE di RINASCITA, quale la nascita del Botticelli "di Venus".
Etc.L'architetto francese Le Corbusier ha usato il RETTANGOLO DORATO
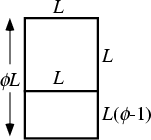nella progettazione del WINDOWS delle sue COSTRUZIONI.I Greci antichi hanno detto che Una DONNA pozzo formato HA AVUTA LE PROPORZIONI MEDIE DORATE. Che cosa fa quella media?
Ricordisi di:
e RAPPORTO: 1/x =
x/(1 + x).Lasci 1 rappresentare LA DISTANZA DALLA PARTE SUPERIORE DELLA TESTA Della DONNA SHAPELY al SUO Pancia-tasto; lasci la x rappresentare LA DISTANZA FRA il SUO Pancia-tasto E I SOLES dei SUOI PIEDI. ALLORA la SUA ALTEZZA È 1 + x, in modo da ha le PROPORZIONI DELLA MEDIA DORATA. Il SUO Pancia-tasto è IL PUNTO MEDIO DORATO. (Veda che vi ho detto che "i pancia-tasti schiocchino verso l'esterno"!)
Sandro Botticelli (1445-1510) ha usato quelle proporzioni nel disegno della figura di Venus nel suddetto imaged della pittura. Conosciamo questo perché, in suo libro, Le Curve di Life (1979), Theodore Cook hanno suddiviso la figura di Venus nella pittura di Botticelli. Cook ha misurato il RAPPORTO: (ombelico alla parte superiore di head)/(navel ai piedi) =
5/(4 +
5) = 5/6
= 1/, quello è 1:
in modo che her length is 1 + , la PROPORZIONE MEDIA
DORATA (DEVINE)!Inoltre avete visto questa proporzione quando avete estratto la stella del cinque-punto. Ogni intersezione di un segmento da un altro segmento in esso divide il segmento intersecato nella proporzione dorata.
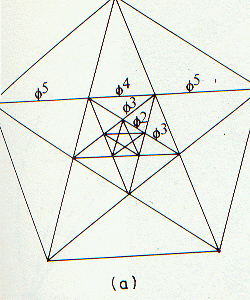
CHE COSA È IL PUNTO DEL TUTTO QUESTO?"Ottenere il la maggior parte per il più minimo", il DIO e gli artisti e gli assistenti tecnici USA I NUMERI IRRAZIONALI!!! Un NUMERO IRRAZIONALE (TRANCENDENT) SELEZIONA Un PUNTO Di BELLEZZA O Un SEGMENTO Di BELLEZZA O Una SUPERFICIE Di BELLEZZA.
Per, un altro esempio della bellezza della natura è una bolla del sapone: una SUPERFICIE DI CURVATURA MINIMA ha formato dalla pellicola del sapone. La bolla più semplice è una singola SFERA, che -- come il CERCHIO -- è costruito come MULTIPLO del numero irrazionale,
. Le forme più complicate accadono quando le bolle multiple si uniscono insieme.Due problemi in sospeso "della bolla":
- per trovare le disposizioni con il più piccolo perimetro (problema planare)
- o più piccola l'area (problema di zona)
che accludono e separano le dati unità di superficie o volumi di numero n = 2, i problemi è richiesta "la doppia congettura della bolla" e la soluzione sia al problema planare che al problema di zona è conosciuta per essere la doppia bolla. Inoltre, la doppia bolla è conosciuta per essere minimizzazione di zona ("più-meno"). Ma non deve ancora sapere se la bolla triplice è minimizzazione di zona.
La ricerca della bolla è stata iniziata dal fisico belga, il Joseph Plateau (1801-1886). E molti problemi relativi sono ancora non risolti -- "la bellezza inscrutabile".
Avete notato "gli arcobaleni" sulla superficie delle bolle del sapone? Quel esposizioni voi che l'arcobaleno inoltre è costruito attraverso "i mezzi irrazionali".
Ripetendo, "per ottenere il la maggior parte per il più minimo", DIO e gli artisti ed i NUMERI IRRAZIONALI di USO degli assistenti tecnici (TRANSCENDENT)!!!Tutto questo e PIÙ, sono venuto tramite IL CANCELLO QUADRATO.