BOLTZMAN'S DERIVATION OF THE MOST PROBABLE DISTRIBUTION OF MOLECULES IN A
SYSTEM (according to Gerhard A. Blass, Theoretical Physics, pp.236-43)
In general, a system of N molecules with certain properties
(total enery content, volume occupied, etc.) can exist in variously diverse states, some many in
type, others few. The type of state most assumed is "the most probable one", from
which deviations are possible, but -- because of the multitude of molecules involved
(1 mole = 6 x 1029 molecules) -- the law of large numbers
of proability theory implies that such deviations are of very low probaility.
The tendency of a system to move toward the most probable state is equivalent to the second
law of thermodynamics: entropy does not macroscopically decrease. So, in calculating this
most probable state, Boltzmann was dealing with the foundations of thermodynamics.
- Start with a system of N molecules whose
representative points move through phase space, subdivided into numbered cells
of unequal size,

 i, each containing unequal numbers of representative points
, Ni.
i, each containing unequal numbers of representative points
, Ni.
- The probability of this arrangement, for equal size cells, is:
P = N!/
 Ni!
.
Ni!
. - For unequal size cells, modify the numerator by a factor,
(

 i)Ni
i)Ni
- This yields the following probability: P = N!
 (
(
 i)Ni/
i)Ni/ iNi!.
iNi!.
- In maximizing such a probability, we conveniently
substitute a continuous density function:
Ni  f(i)
f(i) 
 i
i  D.
D.
- And replace the factorial by the appropriate
Sterling approximation: N! = (N/e)N, for exponential
, e, which, upon substitution of numerator and denominator of
probability fraction, divides out.
- Also the

 i to power f(i)
i to power f(i) 
 i divides out of numerator and denominator,
yielding:
i divides out of numerator and denominator,
yielding:
P = NN/ f(i)D.
f(i)D.
- We can then apply Boltzmann's form for entropy, with
Boltzmann's constant, k:
S = k ln P - k N ln N - k (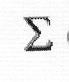 D) ln f(i).
D) ln f(i).
- Now we vary the density factor.
f(i), to maximize entropy, S, or, more conveniently,
to minimize - S/k. To do so, we keep total number of molecules
, so that
 N = 0; and total energy constant
:
N = 0; and total energy constant
:  U = 0. Minimization then leads to -
U = 0. Minimization then leads to -  S/k +
S/k + 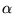
 N +
N +
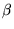
 U = 0.
U = 0.
- This leads to a term,
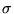 =
= 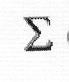 exp(-
exp(- 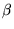 u(i), with
S =
u(i), with
S = 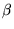 k U + k N ln
k U + k N ln 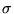 .
.
- Then we arrive at Boltzmann's most probable distribution of molecules in a system:
S = U/T + k ln 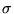 , where
, where 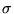 = exp{{u(i)/kT)
= exp{{u(i)/kT)
 i).
i).
- However, a DIMENSIONAL PROBLEM ARISES IN THIS LAST EQUATION, OVERLOOKED BY
BOLTZMANN, OVERLOOKED BY PHYSICISTS OF HIS TIME AND LATER, DOWN TO OUR TIME, EXCEPT FOR BLASS!
The single term on the left-side of the equation, namely, entropy, has the
dimension of energy divided by temperature, which is exactly the dimension of the
first term on the right-hand side. And also part of the second (additive) term on the right-hand
side, namely, k N. But this requires that the rest of the part, namely,
ln
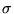 must be dimensionless! which it is not!
Rather, since it denotes
must be dimensionless! which it is not!
Rather, since it denotes 
 i, it has dimensions of the
phase-space volume, i.e., the dimension of action, the dimension of Planck's
constant. How can this part be rendered dimensionless within the equation?
i, it has dimensions of the
phase-space volume, i.e., the dimension of action, the dimension of Planck's
constant. How can this part be rendered dimensionless within the equation?
- When dS= dQ/T is integrated, it can have a constant of
integration. Let it have the dimension of action, which is that of Planck's
constant: h. Then, we can find: S = U/T + k ln
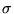 /hd, where d denotes the
number of dimensions on which the molecules move.
/hd, where d denotes the
number of dimensions on which the molecules move.
- Thus, BOLTZMANN'S MOST PROBABLE DISTRIBUTION OF MOLECULES IN A SYSTEM DEMANDS SOMETHING
REPRESENTING PLANCK'S CONSTANT! Attention to dimension analysis and constants of
integration -- matters often ignored by physicists -- would have exposed this many years
before Planck's work! And in statistical mechanics, instead of the crossblend of
thermodynamics and optics that Planck dealt with.
 f(i)
f(i)  D.
D. N = 0; and total energy constant
:
N = 0; and total energy constant
:  U = 0. Minimization then leads to -
U = 0. Minimization then leads to -  S/k +
S/k + 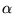
 N +
N +
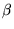
 U = 0.
U = 0.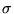 =
= 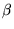 u(i), with
S =
u(i), with
S = 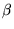 k U + k N ln
k U + k N ln 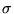 .
.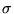 , where
, where 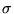 = exp{{u(i)/kT)
= exp{{u(i)/kT) i).
i).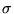 must be dimensionless! which it is not!
Rather, since it denotes
must be dimensionless! which it is not!
Rather, since it denotes 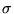 /hd, where d denotes the
number of dimensions on which the molecules move.
/hd, where d denotes the
number of dimensions on which the molecules move.