(MATHEMATICS BEHIND "CANDY MISER'S PUZZLE")

Mathematicians and students today extensively apply the
right triangle in geometry and trigonometry using the "Pythagorean
Formula" to relate lengths of the triangle's SIDES (a, b) and DIAGONAL
(c): a2 + b2 = c2. However, Pythagoras
did not discover this formula, but apparently learned it in his travels  through
Egypt and Mesopotamia. Nevertheless, number triplets {a,b,c} fitting
the formula -- for example, {3, 4, 5}, {5, 12, 13}, etc. -- are today
labeled "Pythagorean triplets". Here's what we know of this subject, and
its consequences.
through
Egypt and Mesopotamia. Nevertheless, number triplets {a,b,c} fitting
the formula -- for example, {3, 4, 5}, {5, 12, 13}, etc. -- are today
labeled "Pythagorean triplets". Here's what we know of this subject, and
its consequences.
Knowledge of Egyptian mathematics derives from two artifacts, The
Rhynd Papyrus (named for its donor to The British Museum) and The
Moscow Papyrus (now in Museum of Fine Arts, Moscow, Russia). Both apparently
derive from a period between 2000 B.C. and 1580 B.C. They describe ability
to solve linear (first degree) equations in one unknown, but no
evidence of solving second degree equations or formulas such as
"The Pythagorean". The Egyptians deal with fractions by adding
unit fractions, such as 1/2, 1/3, 1/4, 1/5, etc. (You use "Egyptian
fractions" nearly every day -- in "making change in commercial transactions".
Thus, a penny = $1/100; a nickel = $1/20; a dime = $1/10; a quarter = $1/4;
a fifty-cent piece = $1/2.) Later we'll see how the "Egyptian fraction"
format extends to the best test of irrationality of numberness.
The Tablet known as "Plympton 322" (created between 1900 B.C. and 1600
B.C.) contains the "Pythagorean" Formula and displays many "Pythagorean
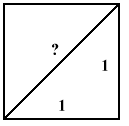
triplets", as well as a diagrammatic proof of the formula. (The AREA of
the SQUARE built on the TRIANGLE'S VERTICAL SIDE, combined with the AREA
of the SQUARE built on its HORIZONTAL SIDE, equals the AREA of the SQUARE
built on THE TRIANGLE'S DIAGONAL. The "Pythagorean"
formula was discovered circa 2000 B.C. in Babylonia or Egypt or both. We
know about its Babylonian origin from approximately half of a million clay
Babylonian tablets engraved in their written cuneiform script, excavated
since the first half of the 19th century (exhibited in the great museums
of Paris, Berlin and London as well as the archeological exhibits at Yale,
Columbia and the University of Pennsylvania). Some 400 of the tablets list
mathematical problems and mathematical tables. They show, for example,
that Babylonian priests had an iterative algorithm for finding square
roots of all numbers -- including the square root of 2 -- to any
desired approximation.
The "Pythagorean"
formula was discovered circa 2000 B.C. in Babylonia or Egypt or both. We
know about its Babylonian origin from approximately half of a million clay
Babylonian tablets engraved in their written cuneiform script, excavated
since the first half of the 19th century (exhibited in the great museums
of Paris, Berlin and London as well as the archeological exhibits at Yale,
Columbia and the University of Pennsylvania). Some 400 of the tablets list
mathematical problems and mathematical tables. They show, for example,
that Babylonian priests had an iterative algorithm for finding square
roots of all numbers -- including the square root of 2 -- to any
desired approximation.
In the absence of mathematical means of investigating motion, the ideas of philosopherCirca 540 B.C.: Tenure of Pythagoras (580-496 B.C.) in Crotona, teaching this Formula, along with his digital geometry, which (implicitly) treats NUMBER AS MAGNITUDE ("muchness" of "anything"), of both SPACE and TIME. The "problem of the gate" upset Pythagorean mathematics and gave support to his philosophical enemies.
Circa 450 B.C., Parminides of Elea challenged the Pythagorean ideas of multiplicity and change with unity and permanence, even arguing that the changes and motions we see in the world are ILLUSORY. Parmenides' disciple, Zeno propounded his "Paradoxes" to further challenge Pythagorean digital geometry and NUMBER AS MAGNITUDE, reserving GEOMETRIC UNITS for this purpose
.420 B.C., Hippias (460-400 B.C., Pythagorean follower) is said to have discovered incommensurability of square root of 2 and to have given proof of this..
Circa 390 B.C., Pythagorean scholar and student of Hippias, Theatetus (described by Plato in "Dialogue" by that name), teaches about "incommensurability". Also taught by Theodorus of Cyrene. Circa 365 B.C., Eudoxus (c. 408-355 B.C.) -- considered with Archimedes
(287-212 B.C.) as "greatest ancient mathematicians" -- taught in Plato's School that MAGNITUDE should only be defined GEOMETRICALLY and created a ratio of magnitudes and a proportion, which comprehended both commensurable and incommensurable ratios (anticipating the work of 18th and 19the century mathematicians). This led to 2000 years of domination of MATHEMATICS by GEOMETRY. And led Plato to argue that proclaiming arithmetic incommensurables implies that motion ("geometry set to time") cannot be arithmetized -- meaning no measures of speed, acceleration, force, etc. -- causing a 1900-year neglect of theoretical mechanics in Europe, postponing "The Industrial Revolution" and prolonging slavery.
Eudoxus also created the geometric method of exhaustion, whereby, for example, a sequence of polygons of increasing sides can "exhaust" (or approach the structure of) the circle. (This anticipates "the integral calculus" in the 17th century -- and a step toward vindication of Pythagorean Arithmetic)
.
 Aristotle
(384-322 B.C.) gained dominance in physics, particularly his "Law
of Falling Bodies": an object fell to the earth according to its weight -- the heavier,
the faster the fall. Over the centuries, a few sceptics individually pointed out a "paradox"
in this notion. Given a 2-unitweight object and a 1-uniweight one, the first should,
by this "Law" fall much faster than the second (numerical proportions were ignored). Tied
together, the 3-unitweight object should fall FASTER than the 2-unitweight object, but --
at the same time -- SLOWER, since the 1-unitweight object should hold back the 2-unitweight
object. But such cavilling was ignored.
Aristotle
(384-322 B.C.) gained dominance in physics, particularly his "Law
of Falling Bodies": an object fell to the earth according to its weight -- the heavier,
the faster the fall. Over the centuries, a few sceptics individually pointed out a "paradox"
in this notion. Given a 2-unitweight object and a 1-uniweight one, the first should,
by this "Law" fall much faster than the second (numerical proportions were ignored). Tied
together, the 3-unitweight object should fall FASTER than the 2-unitweight object, but --
at the same time -- SLOWER, since the 1-unitweight object should hold back the 2-unitweight
object. But such cavilling was ignored.
Circa 300 B.C., in Alexandria, Egypt, Greek Euclid (450-380 B.C.) published his
Elements of Geometry,  culminating
the work of Thales, Pythagoras, Eudoxus, and others. (Only The Bible
has appeared in more copies than The Elements.) Experts attribute
the first four Books to the work of Pythagoras. And the Book Five contains
the great work of Eudoxus on proportions
culminating
the work of Thales, Pythagoras, Eudoxus, and others. (Only The Bible
has appeared in more copies than The Elements.) Experts attribute
the first four Books to the work of Pythagoras. And the Book Five contains
the great work of Eudoxus on proportions
The great Alexandrian Period (332 B.C.-420 A.D.) steam cars lurched
down the streets and giant robots moved arms under steam propulsion, scaring
the faithful. Imperial Roman engineers developed efficient windmills and
water mills (For example, in the first century B.C., the Roman engineer
Vitrivius described the undershot water wheel, later so useful in
medieval and post-medieval Europe, yet rarely used by Romans.) These efficient
watermills and windmills could have replaced the slave-power of the time.
But, with no theoretical mechanics to show this and give hope of
improvements, slavery continued in Europe for hundreds of more years.
415 A.D., in Alexandria, Egypt, Christian mobs assassinated Hypatia Circa 220
B.C., Archimedes refined the Eudoxian method of exhaustion to approximate the area of
a circle, an early estimate of p (ratio of circumerence to diameter
of a circle -- a further step toward "the integral calculus", vindicating Pythagorean
Geometric-Arithmetic.
Circa 220
B.C., Archimedes refined the Eudoxian method of exhaustion to approximate the area of
a circle, an early estimate of p (ratio of circumerence to diameter
of a circle -- a further step toward "the integral calculus", vindicating Pythagorean
Geometric-Arithmetic. ,
greatest woman mathematician of ancient times. A few days later, these
mobs burned the Library of Alexandria (greatest ancient repository of mathematics
and science writings) -- destroying all the works of Eudoxus and almost
all of those of Archimedes, as well as the works of so many other creators
,
greatest woman mathematician of ancient times. A few days later, these
mobs burned the Library of Alexandria (greatest ancient repository of mathematics
and science writings) -- destroying all the works of Eudoxus and almost
all of those of Archimedes, as well as the works of so many other creators
In 527 B. C. Justinian, Roman Emperor of the West wing of the Roman Empire, became also Emperor of the East. He decided that the "pagan" learning of the Academy founded in Plato's name and other philsophical schools threatened orthodox Christianity, so, in 529, all these schools were closed, effectively ending speculative research in Europe. The challenge was taken up by Islamic scholars who not only preserved the knowledge of the ancients but advanced it in "forbidden areas".One of the greatest was the astronomer Mohammed ibn Musa al-Khowarizmi (circa 825 A.S.)
whose name inspired the label "algorithm" for a "sure-fire" method for problem-solving. And the title of his book on Arithmetic inspired our word for "algebra". (Evidence recently emerged that pre-Renaissance Islamic -- and perhaps Jewish -- scholars made discoveries later attributed to European scholars in the Renaissance period.)
The most important Islamic advance was to arithmetize motion and challenge the Aristotlean "Law of Falling Bodies". Peculiarly, Islamic arguments for arithmetizing motion derived from analogies in pharmacy and optics. It appeared possible to change magnitudes in medicines and in light intensities, hence, it was extrapolated to motion.
In this "Medieval-Renaissance" period, Arabic artists excelled in the geometric art of figrative adornment. The finest example of this is The Alhambra in Grenada (Spain), a fortess and palace. Mathematicians recognize 128 distinct patterns of "the wallpaper-tile group". All of these appear in the decorations of The Alhambra (as in an Alhambra portal or an Alhambra relief or an Alhambra mosaic).
As you may read in The Medieval Machine: The Industrial Revolution of the Middle Ages, by Jean Gimpel, 1977, in the 12th century (A.D.) began what should be called "The Mechanical Industrial Revolution". Monks -- desiring to raise their food and other needs, yet have time for prayer and meditation -- were given special permission by the Pope to read pagan texts showing how to build watermills and windmills. In this century and the next, these mills spread across Europe. (The Domesday Book of 1086 lists 5624 water-wheel driven mills in England south of Trent, or about one mill for each 400 persons.) Clearly, further extension of these mills would have eliminated much of the slavepower then existing, but "the lesson" was still not obvious enough.
In 1202, Fibonacci (a.k.a. Leonardo of Pisa) published Liber abaci ("book of the abacus"), the first European books to use decimal notation in arithmetic (which Fibonacci learned in his native North Africa). The spread of decimal arithmetic made possible the great "Age of Navigation" and "Age of Trading", which followed -- although historians choose to ignore this.
William of Ockam (1280?-1349?), sketches notion of inertia, a physical concept later credited to Newton. (The charactor of William of Baskerville played by Sean Connery in the film, The Name of the Rose, was modeled on Ockam.) Jean Buridan (1295?-1359), French philosopher, in 1350's developed the notion of impetus, a physical concept close to the concept of inertia
.1320 A.D., Thomas Bradwardine (1290-1349) studied at Merton College Oxford, became chancellor of St. Paul's Cathedral. Bradwardine was a noted mathematician as well as theologian, known as 'the profound doctor'. Bypassing both the Platonic and Aristotlean traditions, Bradwardine studied bodies in uniform motion and ratios of speed in the treatise De proportionibus velocitatum in motibus (1328). Bradwardine was one of the '''Oxford Calculators''', of Merton College, Oxford University, studying mechanics with William Heytesbury, Richard Swineshead, and John Dumbleton. The Oxford Calculators distinguished '''kinematics''' from '''dynamics''', emphasizing kinematics, and investigating '''instantaneous velocity'''. They first formulated the '''mean speed theorem: a body moving with constant velocity travels distance and time equal to an accelerated body whose velocity is half the final speed of the accelerated body'''. They also demonstrated this theorem -- essence of "The Law of Falling Bodies" -- long before Galileo is credited with this. In '''Tractatus de proportionibus''' (1328), Thomas Bradwardine extended Eudoxus' '''theory of proportions''' to anticipate the concept of '''exponential growth''', later developed by the Bernoullis and Euler, with '''compound interest''' as a special case.Bradwardine became Archbishop of Canterbury in 1349 but died, a month later, of the Black Plague. Bradwardine is mentioned (as "Bisshop Bradwardyne") in Chaucer's Canterbury Tales, in "The Nun's Priest's Tale", line 476.
This Mechanical Industrial Revolution (described above) waned with "The Black Death" (bubonic plague), peaking in 1348. The Black Death was caused by the dearth of cats to control the rat population. For centuries, the superstitious had killed cats, alleging them to be the "familiars" of witches. (Cats' eyescan catch any light in a dark room or cave, lighting up when nothing else does. Also, in cold climes, stroking a cat invokes static electricity, and the sparks scintillate in the dark.) One Pope even advocated exterminating cats. So, by the middle of the 14th century, the dearth of cats allowed the rat population to multiply to epidemic proportions. The rats
carried fleas. And the fleas carried the Plague. In 5 years, the Plague killed 25 million, 1/3 of Europe's Population. In some regions, 50% of the population died in "The Black Death". Many regions lacked blacksmiths, coopers, wheelrights, other craftsmen.
Training had been oral. The Church now allowed more general reading of "pagan" books, initiating The Renaissance. (Tell this story to teen-agers who "want to work with their hands", but ask why they need reading skills!)
Chronology, continued.