I extended the familiar bracket form to encompass the case of interchanging "carriers" with subscripts. Thus, [a,b]_ij a_i b_j - b_ia_j.

This was to encapsulate the outerproduct (of multivector theory), in my special derivation of outerproduct. It's natural that this bracket should also apply to the standard vector cross product, since the latter is the dual of outerproduct.

Given unit basis vectors: i = (1,0,0); j = (0,1,0); k = (0,0,1). Consider A A₁i + A₂j + A₃k; and B B₁i + B₂j + B₃k. Form A X B = (A₂B₃ - B₂A₃) i + (A₃B₁ - B₁A₃)j + (A₁B ₂ - B₁A₂)k = [A,B]₂₃i + [A,B]_3l j + [A,B]₁₂k. (Clearly, a "cyclic pattern", easy to remember.)

The partially implicit cyclic pattern becomes explicit if we use a single unit basis vector carrier, with subscripts: i b ₁; j b₂ ; k b₃. (The standard i, j, k derive from W. R. Hamilton, for his quaternions, with a fourth basis vector.).

Now we can write: A X B = (A₂B₃ - B₂ A₃) b₁ + (A₃B₁ - B₁A₃ ) b₂ + (A₁B₂ - B₁A₂) b ₃ = [A,B]₂₃ b₁ + [A,B]₃₁ b₂ + [A,B]₁₂ b₃. Such a cyclic pattern would be easy to understand and to remember. (Please note the special treatment necessary for cases such as the quantic operator for angular momentum, as explcated below.)

Since my bracket higlights the cyclic pattern of these relations, it can make the presentation of (classical) angular momentum easier to understand and remember. L = r X p, for radius vector ("lever arm"), r, and linear momenum, p.

In components this is usually written:

        Lx = ypz - zpy   Ly = zpx - xpz   Lz = xpy - ypx

Let's rewrite coordinates as basis elements: x y z b₁ b₂ b₃ and L_x L _y L_z L₁ L₂ L₃. Then we have:

        L1 = b2p3 - p2b2   L2 = b3p1 - p3b1   L3 = b1p2 - p1b2

Or:

        L1 = [b,p]23   L2 = [b,p]31   L3 = [b,p]12

The quantic operator for angular momentum is p _x = -i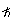D_x, where I use genuine operator notation for partial differentiation, instead of the confusing fractional notation. Now, L_x = -i(y D_z - z D _z). To avoid a confusion of scope invoked by the permutation , we adopt a standard device for writing the partial derivative operator, in such cases, writing D().

Then we can translate classical angular momentum into quantic as L₁ 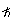= -i[b, D()]₂₃ = -i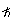(b₂ D_e() - D₁() b₃) . Similarly, L₂ = -i[b,D()]₃₁, and L ₃ = -i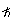[b,D()]₁₂ .