Below, we'll need a consequence of the ROTATION OPERATOR, R -- usually formulated as a matrix in cos q, sin q.
SV PRINCIPLE: A SCALAR is a structure INVARIANT for q = 0 (or R as THE IDENTITY), whereas a VECTOR is INVARIANT whenever DETERMINANT |R| = +1. I'm DERIVING the (EUCLIDEAN) INNER PRODUCT (a.k.a. SCALAR PRODUCT) OF VECTORS, familiar in The Literature. Typically, THE LAW OF COSINES is DERIVED FROM INNER PRODUCT. But I, UNIQUELY, reverse this procedure --DERIVING by two MOTIVES:
Given a minimum of analytic or coordinate geometry (and associated algebra), Augustin Cauchy (1789-1857) taught us how to derive all of trigonometry.
From this, other equivalences of trig will follow. We can obtain The Law of Cosines as generalization of the above Pythagorean Relation. Now consider this D:
(In The Literature, vectors are sometimes denoted by overscore -- difficult in HTML. I adopt the convention of vectors denoted by underscore, scalars without it.) Consider, now, a VECTOR TRANSFORMATION of this D, for vectors a, b, c, such that we have the vector difference:
We wish to interpret [2] in terms of [1], in TRANSFORMING AN UNDIRECTED D INTO A DIRECTED D.
ASSIGNMENT: Improve REASONING and LANGUAGE of this DERIVATION.
Even at this limited stage of OPERATIONS, we'LL show how MULTIVECTOR THEORY can create a POWERFUL STRUCTURE (much used in QUANTUM MATHEMATICS) much more easily than the standard MATRIX THEORY that is invoked. We show how to create IDEMPOTENTS.
What's an IDEMPOTENT? Wots it gud fer? AN IDEMPOTENT (in ARITHMETIC or ALGEBRA) is an ELEMENT WHOSE SQUARE EQUALS ITSELF. You already know two IDEMPOTENTS in ARITHMETIC: 0 and 1.
Thus 0 · 0 = 0; and 1 · 1 = 1. 0 is THE IDENTITY ELEMENT OF ADDITION (AND THE ADDITIVE GROUP); 1 plays those roles for MULTIPLICATION
(and THE MULTIPLICATIVE GROUP). Let's say these are "the improper idempotents". Let's construct a PROPER IDEMPOTENT, then explain its use.
We take a BASIS ELEMENT, say, d3 (a UNIT in "the z-direction" in CARTESIAN COORDINATES, but here no special coordinates are considered). We form a LINEAR VECTOR TERM: a + bd3. We form its square, and see if values for the coefficients will lead to an IDEMPOTENT.
(a + bd3) · (a + bd3) = a2 + 2abd3
+ b2 º a + bd3 → (a2 + b2) + 2abd3 º a + bd3.
Let's equate scalar terms on both sides of "equals", and equate vector terms on both sides: (scalar:) a2 + b2 = a;
(vector:) 2abd3 = bd3.
The vector term simplifies by dividing "out" bd3 on both sides: 2a = 1 -> a = 1/2.
We substitute this in the scalar equation: a2 + b2 = a -> (1/2)2 + b2 = 1/2 ->
b2 = 1/2 - 1/4 -> b2 = 1/4 -> b = 1/2. So we've found a = b = 1/2. Then our term is 1/2 + 1/2d3.
ASSIGNMENT: Find that (1/2 + 1/2d3) · (1/2 + 1/2d3) = 1/2 + 1/2d3. Show also that 1/2 - 1/2d3 is IDEMPOTENT. And show that it is the INVERSE of the other
one, that is, their product equals one.
So this is a PROPER IDEMPOTENT, and other such can be constructed. Wots it gud fer? Any CLOSED
SET INCLUDING THESE CAN BE FORMED INTO A GROUP. Similarly for other PROPER IDEMPOTENTS.
INNER PRODUCT has a special property which tells us something about OUTER PRODUCT and MULTIPRODUCT.
The ROTATION OPERATOR, R, is a SPECIAL CASE of AN ORTHOGONAL TRANSFORMATION, PRESERVING SCALE.
TRANSFORMATION INVARIANT: A SCALAR PRESERVED BY A SCALE-PRESERVING TRANSFORMATION.
Hence, INNER PRODUCT IS A TRANSFORMATION INVARIANT:
a · b = aibi = a'ib'i = OijOikajbk =
Sijajbk = akbk. [5] You also find that the square of a vector is equivalent to its inner product; and its length is square root of the latter -- both STRUCTURES PRESERVED BY INNER PRODUCT.
This INVOKES THE DEFINITIVE CHARACTERISTIC OF EUCLIDEAN SPACE. For (as Henri Cartan notes) a point in n-dimensional Euclidean space can be defined as a set of numbers (coordinates), [x1, x2, ..., xn], such that the distance of this point [x] to the ORIGIN, namely, [0,0,...,0] -- or, equivalently, the self inner product
x x of the vector x, from point x to point 0 -- is given by THE FUNDAMENTAL FORM:
But pseudo-Euclidean spaces (as required, say, in relativistic space-time) may have a DIFFERENT FUNDAMENTAL FORM:
Clearly, [7] cannot be CONSTRUCTED BY INNER PRODUCT. So, ANOTHER TYPE OR VECTOR PRODUCT IS REQUIRED. MY UNIQUE DERIVATION OF OUTERPRODUCT.
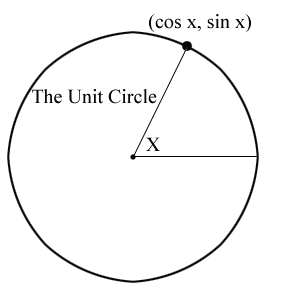 Let x = q. Then, x2 + y2 = 1 → cos2 q + sin2 q = 1.
Let x = q. Then, x2 + y2 = 1 → cos2 q + sin2 q = 1. Taking c = h1, a = h2, b = b1, Ð b1h2 = q = C, we can render this formulation of The Law of Cosines:
Taking c = h1, a = h2, b = b1, Ð b1h2 = q = C, we can render this formulation of The Law of Cosines:
c2 = a2 + b2 — 2 a b cos C [1]
c = b — a [2].
c·c =
(b — a)·(b — a) → c·c =
b·b — a·b —
b·a + a·a. [3]
x = x21 + x22 + ... + x2n = x · x. [6].
x = x21 + x22 + ... + x2n—k — x2n—k+1 — ... — x2n. [7]