We established certain algebras.

WE ESTABLISH PRE/MEET JOIN AND MEET ALGEBRAS, with 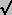, , 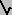, , 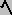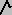as binary operators on integers:

• AFTERMEET ALGEBRA (PM): a 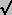b º lub{x| a Ù b = a Ù x};
• AFTERJOIN ALGEBRA (PJ): a 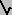b º glb{x| a Ú b = a Ú x};
• PREMEET ALGEBRA (AM): a 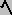b º lub{x| a Ù b = b Ù x};
• PREJOIN ALGEBRA (AJ): a 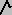b º glb{x| a Ú b = b Ú x}.

We derive many consequences from these P/A J-M Algebras, among them the following.

---

The following shows that JOIN-MEET Algebra is an algebra of algebras.

d(PM) = AM, d(AM) = PM, d(PJ) = AJ, d(AJ) = AJ.

TRANSPOSITION º t: t(PM) = PJ, t(PJ) = PM, t(AJ) = AM, t(AM) = AJ.

TRANSPOSITION º t: t(BJ) = BR, t(BR) = BJ, t(AR) = AJ, t(AJ) = AR.

INVERSION º s = dt = td.

IDENTITY º i = dd = tt = vv.

This can be graphed:

			PM<--d--->PJ
                          ^ \   /^
                          | s\ / |
                         t|   \  |t
                          |  / \ |
                          | /s  \|
                          V      V
                        AM<--d--->AJ

I developed these results in the 70's and wrote an Abstract (labeled for "Hilbert-Skolem Algebras" rather than "JOIN-MEET Algebras") which was published in Notices of The American Mathematical Society. Twenty years later, I discovered ONLINE (in The Standford Encyclopedia of Philosophy) a graph similar to the one above, kwown to Medieval Scholastics as "The Square of Opposition". This, in turn, has important logical connections.

---

The philosophy and logic of the square of opposition began with Aristotle in the fourth century BC in De Interpretatione, which contains three claims: that A and O [below] are contradictories, that E and I are contradictories, and that A and E are contraries. The diagram has appeared in logic texts since that time. Criticized very much in recent decades, it still finds reference.

The square of opposition embodies a group of theses in its diagram -- theses independent of the diagram. The theses specify logical relations for four logical forms:

				NAME		FORM	TITLE
					A	Every S is P	Universal Affirmative
					E	No S is P	Universal Negative
					I	Some S is P	Particular Affirmative
					O	Some S is not P	Particular Negative

The diagram for the traditional square of opposition is:

The theses embodied in this diagram are (for subject S and predicate P):

• "Every S is P" and "Some S is not P" are contradictories.

• "No S is P" and "Some S is P" are contradictories.

• "Every S is P" and "No S is P" are contraries.

• "Some S is P" and "Some S is not P" are subcontraries.

• "Some S is Pis a subaltern of "Every S is P".

• "Some S is not P" is a subaltern of "No S is P".

These theses were explained:

• Two propositions are contradictory iff they cannot both be true and they cannot both be false.

• Two propositions are contraries iff they cannot both be true.

• Two propositions are subcontraries iff they cannot both be false.

• A proposition is a subaltern of another iff it must be true if its superaltern is true, and the superaltern must be false if the subaltern is false.

The main objection to the theses of the SQUARE DIAGRAM is that a term such as "S" could be "empty", that is, have no referent. But this is not crucial. The common modification of these theses is to allow "commuativity" of terms, that is, "S is P", allows consideration of "P is S". Other comments and modifications of the Diagram appear in the Standford reference.

The relevant point for us is that both my diagram and the SQUARE are represented by the Viergruppe. Thus:

			 A<--d--->E
                          ^ \   /^
                          | s\ / |
                         t|   \  |t
                          |  / \ |
                          | /s  \|
                          V      V
                         I<--d--->O

A consequence of this is:

"SQUARE OF OPPOSITION" CAYLEY-TABLE

	d	t	s	i
d	i	s	t	d
t	s	i	d	t
s	t	d	i	s
i	d	t	s	i

As a consequence, THIS BECOMES THE STUDY OF PHILOSOPHICAL PROPERTIES CONSERVED UNDER THE VIERGRUPPE! Assignment: What are these?