- In a SIMPLE (a.k.a. TOTAL)ORDERING (as in COUNTING), of ANY TWO ELEMENTS, one DOMINATES the other.
- Unlike a SIMPLE ORDERING, a PARTIAL ORDERING (PARORDER) can have TWO ELEMENTS SUCH THAT ONE DOES NOT DOMINATE THE OTHER.
- OPERATIONS (e.g., ADDITION, MULTIPLICATION, EXPONENTIATION) WHICH ARE RECURSIVELY GENERATED FROM A SIMPLE ORDERING (e.g., COUNTING) ARE ALSO SIMPLY ORDERED. THEY ARE WELL-DEFINED, WITH UNIQUE INVERSES. THIS IS DESIRABLE IN AN ARITHMETIC.
- OPERATIONS (e.g., JOIN, MEET) IN A PARTIAL ORDERING ARE NOT WELL-DEFINED, SO HAVE NO INVERSES. THIS CAN ALSO BE DESIRABLE IN AN ALGEBRA.
AN ALGEBRA IS AN ARITHMETIC BACKWARDS! For example, 2 + 3 = 5, is like a QUESTION ("2 plus three equals what?") which has an ANSWER ("5"). But x + 3 = 5 is like an ANSWER-FORM ("The sum is 5.") which INDUCES a QUESTION ("What INCREMENTS 3 to become 5?").
Why has this QUESTION only one ANSWER ("2")? BECAUSE (as noted above) THE QUESTION INVOLVES ADDITION, which (as noted above) IS WELL-DEFINED (on a SIMPLE ORDERING), so ONLY ONE ANSWER CAN EXIST: A SINGLETON SET. (For exmple, WELL-DEFINEDNESS OF ADDITION means that, a + b = a + c if, and only if, b = c.)
PARORDERING OPERATIONS (as noted above) ARE NOT WELL-DEFINED, so ALGEBRAICALLY may INDUCE MANY ANSWERS.
Thus, LUB(a,b) = LUB(a,c) DOES NOT FORCE b = c. For example, LCM(7,2) = LCM(7,4) = 14, but, obviously, 2¹ 4. In fact, 14 = LCM(7,2) = LCM(7,4) = LCM(7,8) = LCM(7,16) = .... Any POWER of 2 fits.
The same is the case for GLB. For example, GCD(42,66) = GCD(42,78) = 6, but, obviously, 66 ¹ 78. In fact, 6 = GCD(42,66) = GCD(42,78) = GCD(42,6) = GCD(42,30) = GCD(42,102) = GCD(42,114) = .... Any PRIME MULTIPLE of 6 fits.
The LATTICE SYMBOLS for LUB, GLB are, respectively, Ú, Ù. Hence, we can also write LCM(7,2) = LCM(7,4) as 7 Ú 2 = 7 Ú 4. And we can write GCD(42,66)= GCD(42,78) as 42 Ù 66 = 42 Ù 78.
Also, from what we've learned, we can recast each of the above cases, in ALGEBRAIC FORM:
- 7 Ú 2 = 7 Ú x = 14; solve for INTEGRAL x. This has an INFINITE SET OF SOLUTIONS: THE POWERS OF 2. Perhaps others.
- 42 Ù 66 = 42 Ù x = 6; solve for INTEGRAL x. Again, this has an INFINITE SET OF SOLUTIONS.
WE (UNIQUELY) ESTABLISH PRE-AFTER JOIN AND MEET ALGEBRAS, with
, 
, 
, 
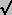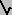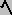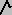, as binary operators on integers:- AFTERMEET ALGEBRA (PM): a 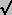b º lub{x| a Ù b = a Ù x};
- AFTERJOIN ALGEBRA (PJ): a 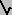b º glb{x| a Ú b = a Ú x};
- PREMEET ALGEBRA (AM): a 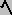b º lub{x| a Ù b = b Ù x};
- PREJOIN ALGEBRA (AJ): a 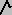b º glb{x| a Ú b = b Ú x}.