B
_________________________________________________________________________________________________
- Baire category theorem
. - A nonempty
metric space (PL) cannot be a ,I>union (PL) of countable (PL) family of
nowhere dense spaces (PL).
- Baire space
. - Any topological space
which is homeomorphic to a complete metric space (PL).
- balanced integer.
- An integer
(PL) is p-balanced for prime p iff, for all binomial coefficients (PL),
C(n,k), k = 0, 1, ..., n (mod p), the number of quadratic
residues (mod p) equals the number of nonresidues.
- Baker-Campbell-Hausdorff series
. - The
series Z = (exeyew), for
noncommuting x, y, w
- ball
. - Interior of a sphere.
- Banach algebra
. - A field (PL)
whose norm makes it a Banach space (PL), with continuous multiplication
(PL).
- Banach space
. - A complete (PL)
vector space (PL) whose topology (PL) is determined by its norm, with
continuous operations.
- Banach-Steinhaus theorem
. - A
pointwise-bounded (PL) family of continuous (PL) linear operators (PL) from
a Banach space (PL) to a normed space (PL) is uniformly bounded.
- Banach-Tarski paradox
. - According to
the Axiom of Choice (PL choice function), a geometric structure the size of the
moon can be dissected into as few as five parts, then reassembled to about the size of a pea
which could be put in a shirt pocket. (For comment on this, see fable.
- bandwidth
. - The range or difference
between the limiting frequencies of a continuous frequency band. In graph theory (PL),
givem L(G) as the set of all distinct integral labelings of the
vertices of graph G, the bandwidth of graph G is minmax|l(u) - l(v)|, for
the length of all edges of the graph.
- Barnette's conjecture
. - Every
3-connected (PL) bipartite cubic planar graph is Hamiltonian.
- barrel
. - A solid of revolution
(PL) with parallel circular top and bottom, common axis, side of a curve symmetrical about the
midplane.
- Barth sextic
. - In complex 3-D
projective space having the maximum possible number of ordinary double points (PL).
Of these, 20 nodes (PL) are at the vertices of a a regular dodecahedron (PL) of
side length 2/f, and 30 are at the
midpoints of the edges of a concentric dodecahedron (PL) of side length
2/f2, for golden ration (PL),
f. Discovered by W. Barth, with implicit
equations: 4(f2x2 - y
2)(f2y2 - z2)(
f2z2 - x2) - (1 + 2f)(x2
+ y2 + z2 - w2)2w2 = 0. The
B. s. is invariant under the icosahedral group (PL). Under the map,
(x, y, z, w)
 (x2, y2, z2, w2)
, the B. s. is the eightfold cover of the Cayley cubic (PL).
(x2, y2, z2, w2)
, the B. s. is the eightfold cover of the Cayley cubic (PL).
- barycenter
. - In complex 3-D projective
space (PL) with the maximum number of double points (PL). Of these, 20 nodes (PL)
are at the vertices of a regular dodecahedron (PL) of side length, 2/f, and 30 are at the midpoints of the edges of a
concentric dodecahedron of side length, 2/f
2, for the golden ration (PL),
- barycenter
. - The centroid (PL) in
a baracentric coordinate system (PL).
- barycentric coordinates
. - Number triples
for masses at vertices of a reference triangle determining centroid of the
three masses.
.
- base
. - The number if digits available
for denoting a number system; base n provides
n digits: 0, 1, 2, ...,n-1. The decimal or denary base
uses ten digits (0,1,2,3,4,5,6,7,8,9). The binary base uses two
digits (0,1). Also known as radix.
- base of a logarithm
. - The arithmetic
operation of exponentiation (bp = x) has two distinct
inverse operations (since it is not commutative): logarithm and root
extraction (PL); bp = x ->
logbx = p. The operand b is the logarithmic
base. The most familiar bases are the exponential number e,
in "natural logarithms"; the number 10 for "common logarithms"; and the number 2 for "information
bits".
.
- base of a number system
. - The number
whose powersplace value (PL) in a positional representation (PL)
of a number system (PL).
- basic polynomial sequence
. - A
polynomial sequence, pn(x) is a b. p. s. for a delta
operator (PL) Q if: p0(x) = t;
pn(0) = 0,
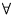 n > 0; Qpnp(x) = npn-1
(x). A b. p. s. for a delta operator is a binomial-type sequence (PL) of
polynomials, and conversely.
n > 0; Qpnp(x) = npn-1
(x). A b. p. s. for a delta operator is a binomial-type sequence (PL) of
polynomials, and conversely.
- basis
. - A set of linearly independent (PL)
ectors in a vector space (PL) such that each vector in the space can be represented as a finite linear
combination of vectors from the basis set. Vectors in the basis are called base vectors.
The number of base vectors is the dimension of the vector space and may be infinite.
- bayesian
. - Treating a probability
(PL) as a degree of belief modifieable by experience in accordance with Bayes' rule (PL).
This contrasts with the frequentist (PL) approach, represents a probability as the relative
frequency of occurrence.
- bei function
. - The imaginary part of Jn(ze±3pi/4)
, where
Jn is the nth Bessel function. PL ber function.
ber function. The real part of Jn(ze±3pi/4), where
Jn is the nth Bessel function. PL bei function.
Bernoulli differential equation. A
linear (PL) differential equation (PL) of the form: Dxy +
yf(x) = yng(x).
Bernoulli's lemniscate. PL
lemniscate.
Bertrand's postulate. For n > 3, there exists at least one prime (PL) between n
and 2n - 2..
Bessel differential equation. x2Dxxy + xDxy + (x2 - m2) = 0
, with regular singularity (PL) at 0, irregular
singularity (PL) at  . Solutions are Bessel functions (PL).
Bessel function. Solutions of Bessel
differential equation (PL). For n a positive or negative integer
, the nth Bessel function, Jn
(x), is the coefficient of tn in expansion
of ex[t - 1/t]/2 in powers of
t, 1/t.
Betti number. A topological invariant
, the maximum numbers that do not divide a surface. The n
th Betti number is the rank (PL) of the nth
homology group (PL)..
biconditional. Statment logic
connective (PL): for statments P, Q, if
P, then Q, and if Q,
then P; symbolized P <-> Q;
Q is a necessary and sufficient condition for
P, and vice versa. Also labeled statement equivalence.
biconnected graph. A graph with
no vertex such that removal of its node would disconnect the graph.
bicorn. Curve with equation: y2(a2 - x2 = (x2 + 2ay - a2)2
.
biharmonic function. A solution of
. Solutions are Bessel functions (PL).
Bessel function. Solutions of Bessel
differential equation (PL). For n a positive or negative integer
, the nth Bessel function, Jn
(x), is the coefficient of tn in expansion
of ex[t - 1/t]/2 in powers of
t, 1/t.
Betti number. A topological invariant
, the maximum numbers that do not divide a surface. The n
th Betti number is the rank (PL) of the nth
homology group (PL)..
biconditional. Statment logic
connective (PL): for statments P, Q, if
P, then Q, and if Q,
then P; symbolized P <-> Q;
Q is a necessary and sufficient condition for
P, and vice versa. Also labeled statement equivalence.
biconnected graph. A graph with
no vertex such that removal of its node would disconnect the graph.
bicorn. Curve with equation: y2(a2 - x2 = (x2 + 2ay - a2)2
.
biharmonic function. A solution of  4 = 0.
bijection. A one-one corespondence
between two setsl equivalently, a function that is both an injection (into) and a
surjection (onto) -- PL both.
bilateral Laplace transform. A
Laplace transform between positive and negative infinity.
bilinear expression. A functional
expression that is separately linear (PL) in each of its two functands (PL).
bilinear function. PLbilinear expression.
bilinear map. PL bilinear expression.
billion A number written 1,000,000,000 =
109.
bimodul (hays). A number system which
bifurcates into two subsystems each of which forms a modul (PL), i.e.,
closed under subtraction. Whereas each system of the naturals, integers, rational,
and reals forms monolithically a modul -- allowing the basic vector
structure of the latter three to be hidden by signs -- by contrast, in
the complex number system, the "imaginary" part forms a modul
which is subtractively closed off from the "real" part, hence, the
vector structure cannot be hidden by mere signs. A consequence is
that a complex number also provides the simplest form of a spinor
(PL) and the basis of a
recursive generation of "the arithmetic of Clifford numbers" or multivectors (PL). Find a
further consequence of bimodulity in Quanta, by P. W. Atkins, p. 81, showing that a
complex wavefunction actually manifests itself as two separate wavefunctions, one
for the real component and one for the imaginary component preceding it in time;
the higher the energy, the faster the wavefunction oscillates between real and
imaginary.
binary number. A number in the
binary number system..
binary number system. A number system
using two as the base (PL), written with only the digits 0, 1..
binary operation. Rule for combining
two elements of a set to yield a third element of the set. (Addition, subtraction, multiplication,
division, exponentiation, logarithm, root extraction.).
binary system. PL binary number.
binary-to-decimal conversion. Transformation (PL)
from a base 2 (binary, PL) number representation (PL) to a base 10 (decimal.
PL) representation.
binary tree. A tree with two
branches at each fork and one or two leaves at each branch.
binomial. A polynomial (PL) consisting
of two terms (PL).
binomial differential equation. (Dxy)m = 0.
binomial equation. PL quadratic equation.
binomial surd. A surd is a root of a
number. A binomial surd is a binomial (PL) of the form ac1/m
+ bd1/n or a + bd1/n, where
m, n are integers greater than 1 and the indicated roots are irrational numbers, while
conjugate binomial surds are pairs of the form a + bd 1/n
and a - bd1/n or ac1/m
+ bd1/n and ac1/m - bd1/n.
binormal. The binormal to a curve at
a point P in 3-D Euclidean space is the vector through
P that is normal to the osculating (PL) plane of the curve at P. The direction of the vector is chosen so that, together with the
positive tangent and principal normal to the curve at P, it forms a
right-handed Cartesian system (PL).
bipartite cubic graph (bicubic graph, Tutti conjecture)
. Tutti (1971) conjectured that all 3-connected (PL) bicubic graphs are
Hamiltonian..
bipartite graph. A set of vertices
disjoined into two sets s. t. no two vertices in same set are adjacent.
biquadratic. A polynomial (Pl) of degree 4.
Also "quartic"..
biquinary abacus. Chinese-style abacus with markers
separated into 2-part and 5-part sections.
biquinary notation. Mixed-based notation of numbers as
represented on a biquinary abacus (PL). Digits are grouped in pairs, the first of which indicates 0 or 1
unit of 5, and the second 0, 1, 2, 3, or 4 units of 1.
birectangular. A geometric structure (not necessarily planar)
with two right angles (PL).
bisector. A line or hyperplane dividing
a given angle into two equal angles. Also, a point, line, or plane passing through the midpoint
of a line segment.
bit. Place value in a
binary number, representing 0 or 1. The basic unit of information in a
digital computing system. (Acronym for binary digit.)
body of revolution. The 3-D
structure formed by rotating a planar curve or planar region about a line (axis of
revolution) in the same plane. Given a closed curve which does not intersect the axis of
revolution, the body of revolution is an annular solid.
boltzmannian theory. A subsystem
of occupancy theory (PL), in turn a subsytem of combinatorics (PL). If b number of boltzmannians in set B are assigned
to a c number of cells in set C,
then the number of possible assignments is cb. This
is homologous to the number of functions from set B to set
C. PL fermions, bosons.
Bolzano's theorem. If
f is real-valued and continuous on the real closed interval [a, b] and f(a) > 0 and f(b) <
0, then there exists some number x0 in the open interval,
(a,b) for which f(x0) = 0.
Bolzano-Weierstrass theorem. For
bounded infinite point set (PL), S, there exists a point
x as limit point (PL) of S. (Usually
credited to Karl (1815-1897) Weierstrass but proved by Bernard Bolzano (1781-1848) in 1817, and
apparently was known to Augustin Cauchy (1789-1857)..
Boolean algebra. A misnomer and
distortion[5] of the work of George Boole (1815-1864). Boole intended to develop
structure homologous to sets with multiple tokens and with signs (positive and
negative). But his untimely death left his work to the distortions of W. S. Jevons. The
system described by this name is a set of elements a, b, c, ...
with binary operators
4 = 0.
bijection. A one-one corespondence
between two setsl equivalently, a function that is both an injection (into) and a
surjection (onto) -- PL both.
bilateral Laplace transform. A
Laplace transform between positive and negative infinity.
bilinear expression. A functional
expression that is separately linear (PL) in each of its two functands (PL).
bilinear function. PLbilinear expression.
bilinear map. PL bilinear expression.
billion A number written 1,000,000,000 =
109.
bimodul (hays). A number system which
bifurcates into two subsystems each of which forms a modul (PL), i.e.,
closed under subtraction. Whereas each system of the naturals, integers, rational,
and reals forms monolithically a modul -- allowing the basic vector
structure of the latter three to be hidden by signs -- by contrast, in
the complex number system, the "imaginary" part forms a modul
which is subtractively closed off from the "real" part, hence, the
vector structure cannot be hidden by mere signs. A consequence is
that a complex number also provides the simplest form of a spinor
(PL) and the basis of a
recursive generation of "the arithmetic of Clifford numbers" or multivectors (PL). Find a
further consequence of bimodulity in Quanta, by P. W. Atkins, p. 81, showing that a
complex wavefunction actually manifests itself as two separate wavefunctions, one
for the real component and one for the imaginary component preceding it in time;
the higher the energy, the faster the wavefunction oscillates between real and
imaginary.
binary number. A number in the
binary number system..
binary number system. A number system
using two as the base (PL), written with only the digits 0, 1..
binary operation. Rule for combining
two elements of a set to yield a third element of the set. (Addition, subtraction, multiplication,
division, exponentiation, logarithm, root extraction.).
binary system. PL binary number.
binary-to-decimal conversion. Transformation (PL)
from a base 2 (binary, PL) number representation (PL) to a base 10 (decimal.
PL) representation.
binary tree. A tree with two
branches at each fork and one or two leaves at each branch.
binomial. A polynomial (PL) consisting
of two terms (PL).
binomial differential equation. (Dxy)m = 0.
binomial equation. PL quadratic equation.
binomial surd. A surd is a root of a
number. A binomial surd is a binomial (PL) of the form ac1/m
+ bd1/n or a + bd1/n, where
m, n are integers greater than 1 and the indicated roots are irrational numbers, while
conjugate binomial surds are pairs of the form a + bd 1/n
and a - bd1/n or ac1/m
+ bd1/n and ac1/m - bd1/n.
binormal. The binormal to a curve at
a point P in 3-D Euclidean space is the vector through
P that is normal to the osculating (PL) plane of the curve at P. The direction of the vector is chosen so that, together with the
positive tangent and principal normal to the curve at P, it forms a
right-handed Cartesian system (PL).
bipartite cubic graph (bicubic graph, Tutti conjecture)
. Tutti (1971) conjectured that all 3-connected (PL) bicubic graphs are
Hamiltonian..
bipartite graph. A set of vertices
disjoined into two sets s. t. no two vertices in same set are adjacent.
biquadratic. A polynomial (Pl) of degree 4.
Also "quartic"..
biquinary abacus. Chinese-style abacus with markers
separated into 2-part and 5-part sections.
biquinary notation. Mixed-based notation of numbers as
represented on a biquinary abacus (PL). Digits are grouped in pairs, the first of which indicates 0 or 1
unit of 5, and the second 0, 1, 2, 3, or 4 units of 1.
birectangular. A geometric structure (not necessarily planar)
with two right angles (PL).
bisector. A line or hyperplane dividing
a given angle into two equal angles. Also, a point, line, or plane passing through the midpoint
of a line segment.
bit. Place value in a
binary number, representing 0 or 1. The basic unit of information in a
digital computing system. (Acronym for binary digit.)
body of revolution. The 3-D
structure formed by rotating a planar curve or planar region about a line (axis of
revolution) in the same plane. Given a closed curve which does not intersect the axis of
revolution, the body of revolution is an annular solid.
boltzmannian theory. A subsystem
of occupancy theory (PL), in turn a subsytem of combinatorics (PL). If b number of boltzmannians in set B are assigned
to a c number of cells in set C,
then the number of possible assignments is cb. This
is homologous to the number of functions from set B to set
C. PL fermions, bosons.
Bolzano's theorem. If
f is real-valued and continuous on the real closed interval [a, b] and f(a) > 0 and f(b) <
0, then there exists some number x0 in the open interval,
(a,b) for which f(x0) = 0.
Bolzano-Weierstrass theorem. For
bounded infinite point set (PL), S, there exists a point
x as limit point (PL) of S. (Usually
credited to Karl (1815-1897) Weierstrass but proved by Bernard Bolzano (1781-1848) in 1817, and
apparently was known to Augustin Cauchy (1789-1857)..
Boolean algebra. A misnomer and
distortion[5] of the work of George Boole (1815-1864). Boole intended to develop
structure homologous to sets with multiple tokens and with signs (positive and
negative). But his untimely death left his work to the distortions of W. S. Jevons. The
system described by this name is a set of elements a, b, c, ...
with binary operators  ("join"),
("join"),  ("meet") obeying an idempotent law: a
("meet") obeying an idempotent law: a  a = a, a
a = a, a  a = a; commutative
laws: a
a = a; commutative
laws: a  b = b
b = b  a,
a
a,
a  b = b
b = b  a; associative laws:
a
a; associative laws:
a  (b
(b  c) = (a
c) = (a  b)
b)
 c, a
c, a  (b
(b  c) = (a
c) = (a  b)
b)  c; distributive laws; a
c; distributive laws; a  (b
(b  c) = (a
c) = (a  b)
b)  (a
(a  c), a
c), a  (b
(b
 c) = (a
c) = (a  b)
b)  (a
(a  c); absorption laws: a
c); absorption laws: a  (a
(a  b) = a
b) = a  (a
(a  b) = a; with univeral bounds
O, I such that O
b) = a; with univeral bounds
O, I such that O  a = O,
O
a = O,
O  a = a, I
a = a, I  a = a, I
a = a, I  a = I; and a unary operation a -> a' such that a
a = I; and a unary operation a -> a' such that a  a' = O, a
a' = O, a  a' = I. Other instances of "Boolean algebras": the subsets
of a set under appropriate set-theoretic operations; a statement logic under its appropriate
operations; a complemented distributive lattice under its appropriate operations. (This
shows that a "Boolean algebra" has some of the general aspects of a repertory -- PL --
without suggestions of educational possibilities and no reference to semiotic transformations.)
Boolean function. Elements of a
Boolean algebra (PL) with unique representation (up to order) as complete products
(PL), for total membership of 2nn.
Boolean ring. A ring (PL) with
unit s.t. every element is idempotent -- applies to Boolean algebra (PL).
Borel algebra. A sigma algebra
(PL) generated by a collection of open sets (PL) (or closed sets, PL).
Borel (probabilty) measure. A measure
(PL) on a Borel algebra (PL): all contiuous functions herein are
measurable.
bordant. Two manifolds forming
boundary of a third manifold.
bordism. Term no replacing
cobordism. PL bordant.
Borel set. Element of a Borel algebra
.
boson theory. A subsystem of
occupancy theory (PL), in turn a subsytem of combinatorics (PL). The members of
a set B, containing b in number,
is assigned to a set C of cells, c in
number, no restrictions on occupancy. (This differs from boltzmannian theory in
that boltzmannians are distinguishable.) The number of possible assignments is
the negative binomial or Pascal distribution: (b - 1)!/(b - c)!(c - 1)!,
where n! = n(n-1)(n-1)...(2)(1), the factorial function (PL).
Example: Let B denote number of indistinguishable passengers on a bus,
and let C denote number of bus stops. (PL fermions.)
In quantum physics, bosons are the carriers of force or interaction between particles.
bottlecap (figurate, Pythagorean) geometry.
Pythagoras created a figurate or discrete geometry of structures outlined by points
(represented by stones, etc.). This is easily taught to children via bottlecaps from soft
drinks. (PL gnomon.)
boundary. The set of all boundary
points (PL) of a given subset of a topological space (PL).
boundary condition. Constraining the
solutions of a system of differential equations in terms a specified set of values of the
independent functand(s), or one or more values of a difference equation or recurrence
relation, in order to initiate the computation.
boundary point. Member of the closure
of a set and of the closure of its complement.
boundary value problem. Solving a system
of differential, integral, or difference equations with its boundary conditions by
requiring the the operators of the system to take on specified values along portions of the boundary
of the space-time solution domain.
bounded function. A real function
f for which there is a positive real number r, bounding f such that f(x) < r for all x
in the domain of f. In general, a function whose range is a
metric space is bounded if an open ball (PL) exists that entirely contains the range of the
function.
bounded set. A set of real numbers
M is bounded above if there exists a real (upper bounding) number
R such that x
a' = I. Other instances of "Boolean algebras": the subsets
of a set under appropriate set-theoretic operations; a statement logic under its appropriate
operations; a complemented distributive lattice under its appropriate operations. (This
shows that a "Boolean algebra" has some of the general aspects of a repertory -- PL --
without suggestions of educational possibilities and no reference to semiotic transformations.)
Boolean function. Elements of a
Boolean algebra (PL) with unique representation (up to order) as complete products
(PL), for total membership of 2nn.
Boolean ring. A ring (PL) with
unit s.t. every element is idempotent -- applies to Boolean algebra (PL).
Borel algebra. A sigma algebra
(PL) generated by a collection of open sets (PL) (or closed sets, PL).
Borel (probabilty) measure. A measure
(PL) on a Borel algebra (PL): all contiuous functions herein are
measurable.
bordant. Two manifolds forming
boundary of a third manifold.
bordism. Term no replacing
cobordism. PL bordant.
Borel set. Element of a Borel algebra
.
boson theory. A subsystem of
occupancy theory (PL), in turn a subsytem of combinatorics (PL). The members of
a set B, containing b in number,
is assigned to a set C of cells, c in
number, no restrictions on occupancy. (This differs from boltzmannian theory in
that boltzmannians are distinguishable.) The number of possible assignments is
the negative binomial or Pascal distribution: (b - 1)!/(b - c)!(c - 1)!,
where n! = n(n-1)(n-1)...(2)(1), the factorial function (PL).
Example: Let B denote number of indistinguishable passengers on a bus,
and let C denote number of bus stops. (PL fermions.)
In quantum physics, bosons are the carriers of force or interaction between particles.
bottlecap (figurate, Pythagorean) geometry.
Pythagoras created a figurate or discrete geometry of structures outlined by points
(represented by stones, etc.). This is easily taught to children via bottlecaps from soft
drinks. (PL gnomon.)
boundary. The set of all boundary
points (PL) of a given subset of a topological space (PL).
boundary condition. Constraining the
solutions of a system of differential equations in terms a specified set of values of the
independent functand(s), or one or more values of a difference equation or recurrence
relation, in order to initiate the computation.
boundary point. Member of the closure
of a set and of the closure of its complement.
boundary value problem. Solving a system
of differential, integral, or difference equations with its boundary conditions by
requiring the the operators of the system to take on specified values along portions of the boundary
of the space-time solution domain.
bounded function. A real function
f for which there is a positive real number r, bounding f such that f(x) < r for all x
in the domain of f. In general, a function whose range is a
metric space is bounded if an open ball (PL) exists that entirely contains the range of the
function.
bounded set. A set of real numbers
M is bounded above if there exists a real (upper bounding) number
R such that x  B for all
x in M. M
is bounded below if (lower bounding) R
B for all
x in M. M
is bounded below if (lower bounding) R  x. Also,
a subset of a metric space is bounded if it can be contained in some open ball of finite radius.
bounded variation. Property of a
function (PL), f(x) if, for the closed interval (PL), [a, b], there exists an L such that
|f(x1) - f(a)| + |f(x2) - f(x1)| + ... +
|f(b) - f(xn-1)| < L.
Bowditch curve. PLLissajous curve
.
Boy surface. A nonorientable surface
(PL) and sextic surface (PL), one of three surfaces produced by a Möboid (Möbius
strip, M. band) (PL) to a disk (PL); the other two are the cross-cap (PL) and the
Roman surface (PL). The B. s. is a model of the projective plane (PL) w/osingularities
. In 1986, contradicting Hopf, F. Apéry showed that the B. s. can generated by the
general method for nonorientable surfaces: f1(x, y, z) = ½
(2x2 - y2 - z2)(x2 + y2 + z2)
+ 2yz(y2 - z2) + zx(x2 - z2) + xy(y2 - x
2), f2(x, y, z) = ½(3)-1/2[(y2 - z2)
(x2 + y2 + z2) + zx(z2 - x2) + xy(y2
- x2), f3(x, y, z) = 1/8(x + y + z)[(x + y + z)3 +4(y -
x)(z - y)(x - z)]. Inserting x = cos u sin v, y = sin u sin v, z = cos
v produces the Boy surface. A homotopy (PL) (smooth deformation) between the
Roman surface and Boy derives from equations: x(u, v) = [(2)
½) cos (2u) cos2 v + cos u sin (2v)]/[2 - a(2)
½ sin (3u) sin (2v)], y(uv) = [(2)½) sin (2u) cos2
v + sin u sin (2v)]/[2 - a(2)½ sin (3u) sin (2v)], z
(uv) = (3 cos 2 v)/[2 - a(2)½ sin (3u) sin
(2v)], a = 0
x. Also,
a subset of a metric space is bounded if it can be contained in some open ball of finite radius.
bounded variation. Property of a
function (PL), f(x) if, for the closed interval (PL), [a, b], there exists an L such that
|f(x1) - f(a)| + |f(x2) - f(x1)| + ... +
|f(b) - f(xn-1)| < L.
Bowditch curve. PLLissajous curve
.
Boy surface. A nonorientable surface
(PL) and sextic surface (PL), one of three surfaces produced by a Möboid (Möbius
strip, M. band) (PL) to a disk (PL); the other two are the cross-cap (PL) and the
Roman surface (PL). The B. s. is a model of the projective plane (PL) w/osingularities
. In 1986, contradicting Hopf, F. Apéry showed that the B. s. can generated by the
general method for nonorientable surfaces: f1(x, y, z) = ½
(2x2 - y2 - z2)(x2 + y2 + z2)
+ 2yz(y2 - z2) + zx(x2 - z2) + xy(y2 - x
2), f2(x, y, z) = ½(3)-1/2[(y2 - z2)
(x2 + y2 + z2) + zx(z2 - x2) + xy(y2
- x2), f3(x, y, z) = 1/8(x + y + z)[(x + y + z)3 +4(y -
x)(z - y)(x - z)]. Inserting x = cos u sin v, y = sin u sin v, z = cos
v produces the Boy surface. A homotopy (PL) (smooth deformation) between the
Roman surface and Boy derives from equations: x(u, v) = [(2)
½) cos (2u) cos2 v + cos u sin (2v)]/[2 - a(2)
½ sin (3u) sin (2v)], y(uv) = [(2)½) sin (2u) cos2
v + sin u sin (2v)]/[2 - a(2)½ sin (3u) sin (2v)], z
(uv) = (3 cos 2 v)/[2 - a(2)½ sin (3u) sin
(2v)], a = 0  R.s., a = 1
R.s., a = 1
 B.s..
boxcar function. The function (PL),
Bc(a, b) = c|H(x - a) - H(x - b)| which is equal to c for a < x < b and zero otherwise, where H(x) is the Heavyside function (PL). The unit rectangle function
is B1(-1/2, 1/2).
brachistochrone problem. To find
curve s.t. a bead sliding down it (from rest) does so in the least time. It is the
cycloid (PL). (PL tautochrone problem.)
bracket. PL commutator..
branch. A maximal subtree (PL)
containing a given point as endpoint.
branch cut. A line in the
complex plane rendering continuous (PL) a multivalued function./DD>
branch of a function. PL branch cut
.
branch point. PL branch.
Brianchon's theorem. The dual
(PL) of Fermat's theorem (PL).
bridge. The edges (PL) of a
connected graph (PL) whose removal disconects the graph.Property of a
functiOn (PL), f(x) if, for the closed interval (PL), [a, b], there exists an L such that
|f(x1) - f(a)| + |f(x2) - f(x1)| + ... +
|f(b) - f(xn-1)| < L.
Brouwer fixed-point theorem. Any
contiuous function has a fixed-point (PL) in a unit n
-ball (PL).
Brownian motion. PL Wiener process
.
Buffon's needle problem.
The probability (PL) P(l, d) that a tossed needle of
length l lands on a grid of equally-spaced lines, a distance
d apart. Solved by naturalist Buffon in 1771.
P(l, d) = 2l/(d p).
bullet nose. Curve of equation a2y2 - b2x2 = x2y
.
bundle. PL fiber bundle.
Burali-Forti paradox. Incompatability of
conditions on transfinite ordinal numbers.
butterfly catastrophe.PL catsastrophe
.
bypass. Melzak: "Homind may have become
human by internalizing bypass." Me: Language became mathematics by formalizing bypass.
B.s..
boxcar function. The function (PL),
Bc(a, b) = c|H(x - a) - H(x - b)| which is equal to c for a < x < b and zero otherwise, where H(x) is the Heavyside function (PL). The unit rectangle function
is B1(-1/2, 1/2).
brachistochrone problem. To find
curve s.t. a bead sliding down it (from rest) does so in the least time. It is the
cycloid (PL). (PL tautochrone problem.)
bracket. PL commutator..
branch. A maximal subtree (PL)
containing a given point as endpoint.
branch cut. A line in the
complex plane rendering continuous (PL) a multivalued function./DD>
branch of a function. PL branch cut
.
branch point. PL branch.
Brianchon's theorem. The dual
(PL) of Fermat's theorem (PL).
bridge. The edges (PL) of a
connected graph (PL) whose removal disconects the graph.Property of a
functiOn (PL), f(x) if, for the closed interval (PL), [a, b], there exists an L such that
|f(x1) - f(a)| + |f(x2) - f(x1)| + ... +
|f(b) - f(xn-1)| < L.
Brouwer fixed-point theorem. Any
contiuous function has a fixed-point (PL) in a unit n
-ball (PL).
Brownian motion. PL Wiener process
.
Buffon's needle problem.
The probability (PL) P(l, d) that a tossed needle of
length l lands on a grid of equally-spaced lines, a distance
d apart. Solved by naturalist Buffon in 1771.
P(l, d) = 2l/(d p).
bullet nose. Curve of equation a2y2 - b2x2 = x2y
.
bundle. PL fiber bundle.
Burali-Forti paradox. Incompatability of
conditions on transfinite ordinal numbers.
butterfly catastrophe.PL catsastrophe
.
bypass. Melzak: "Homind may have become
human by internalizing bypass." Me: Language became mathematics by formalizing bypass.
 (x2, y2, z2, w2)
, the B. s. is the eightfold cover of the Cayley cubic (PL).
(x2, y2, z2, w2)
, the B. s. is the eightfold cover of the Cayley cubic (PL).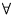 n > 0; Qpnp(x) = npn-1
(x). A b. p. s. for a delta operator is a binomial-type sequence (PL) of
polynomials, and conversely.
n > 0; Qpnp(x) = npn-1
(x). A b. p. s. for a delta operator is a binomial-type sequence (PL) of
polynomials, and conversely. (x2, y2, z2, w2)
, the B. s. is the eightfold cover of the Cayley cubic (PL).
(x2, y2, z2, w2)
, the B. s. is the eightfold cover of the Cayley cubic (PL).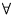 n > 0; Qpnp(x) = npn-1
(x). A b. p. s. for a delta operator is a binomial-type sequence (PL) of
polynomials, and conversely.
n > 0; Qpnp(x) = npn-1
(x). A b. p. s. for a delta operator is a binomial-type sequence (PL) of
polynomials, and conversely. . Solutions are Bessel functions (PL).
. Solutions are Bessel functions (PL). 4 = 0.
4 = 0. ("join"),
("join"),  ("meet") obeying an idempotent law: a
("meet") obeying an idempotent law: a  a = a, a
a = a, a  a = a; commutative
laws: a
a = a; commutative
laws: a  b = b
b = b  a,
a
a,
a  b = b
b = b  a; associative laws:
a
a; associative laws:
a  (b
(b  c) = (a
c) = (a  b)
b)
 c, a
c, a  (b
(b  c) = (a
c) = (a  b)
b)  c; distributive laws; a
c; distributive laws; a  (b
(b  c) = (a
c) = (a  b)
b)  (a
(a  c), a
c), a  (b
(b
 c) = (a
c) = (a  b)
b)  (a
(a  c); absorption laws: a
c); absorption laws: a  (a
(a  b) = a
b) = a  (a
(a  b) = a; with univeral bounds
O, I such that O
b) = a; with univeral bounds
O, I such that O  a = O,
O
a = O,
O  a = a, I
a = a, I  a = a, I
a = a, I  a = I; and a unary operation a -> a' such that a
a = I; and a unary operation a -> a' such that a  a' = O, a
a' = O, a  a' = I. Other instances of "Boolean algebras": the subsets
of a set under appropriate set-theoretic operations; a statement logic under its appropriate
operations; a complemented distributive lattice under its appropriate operations. (This
shows that a "Boolean algebra" has some of the general aspects of a repertory -- PL --
without suggestions of educational possibilities and no reference to semiotic transformations.)
a' = I. Other instances of "Boolean algebras": the subsets
of a set under appropriate set-theoretic operations; a statement logic under its appropriate
operations; a complemented distributive lattice under its appropriate operations. (This
shows that a "Boolean algebra" has some of the general aspects of a repertory -- PL --
without suggestions of educational possibilities and no reference to semiotic transformations.) B for all
x in M. M
is bounded below if (lower bounding) R
B for all
x in M. M
is bounded below if (lower bounding) R  x. Also,
a subset of a metric space is bounded if it can be contained in some open ball of finite radius.
x. Also,
a subset of a metric space is bounded if it can be contained in some open ball of finite radius. R.s., a = 1
R.s., a = 1
 B.s..
B.s..