C
_________________________________________________________________________________________________
- cage graph
. - A v-cage is a v-regular
graph with maximum possible number of nodes.
- calculus
. - The word "calculus" derives from
a Greek word meaning "pebble" or "stone". (This usage appears in medicine, wherein a
gallstone or kidneystone is a calculus.) Presently, "calculus" has the general
meaning of problem-solving procedure, deriving from ancient usage. A Greek shepherd tied
a bag of pebbles to his belt, one pebble for each of his sheep. As he allowed sheep out of a pen,
he would check the correspondence to see if any sheep was missing; similarly, when he again penned
them. In mathematics, the term refers to the differential and integral calculus (PL).
.
- calculus of finite differences
.
- Interpolating difference operators (PL) evaluate functions at points in
arithmetic progression (PL). Includes differentiation and integration analogs.
- calculus of residues
. - Applying
the Cauchy residue theorem (PL) and related theorems of complex analysis (PL)
to evaluate contour integrals (PL), compute residues of meromorphic functions
(PL), and expand series of meromorphic functions (PL).
- calculus of tensors
. - PL tensor.
- calculus of variations
. - Determining
maxima, minima (PL) of a given functional (PL) or a definite integral (PL),
relating to a class of functions or the functands (PL) of the integrand function
(PL). Arose from the 1696 brachistochrone problem (PL) of Johann Bernoulli.
- calculus of vectors
. - PL vector.
- camel problem
. - Traditional mathematics
problem, thought to be Islamic in origin. "An arab riding his camel in the desert encounters
three Arabic youths arguing amid 17 camels. Their deceased father willed only these 17 camels as
their inheritance. The eldest is to receive half of the camels; the second son, one-third of the
camels; the youngest son, one-ninth of the camels. But how allot these portions of 17 camels? The
stranger assigns his camel to the herd, increasing it to 18 camels. Bypassing his own camel, he
assigns 9 camels (1/2 of 18) to the eldest son; 6 camels (1/3 of 18) to the second son; 2 camels
(1/9 of 18) to the youngest son. Then the stranger mounts his own camel and rides away." The
solution is induced by the least common denominator (LCD) (PL) of the portional
fractions, 1/2, 1/3,1/9, namely, 18. That is, 1/2 + 1/3 + 1/9 = 9/18 + 6/17 + 2/18 = 17/18. The
expanded problem (expanding by 1) provides the solution. Canadian mathematician, Z. A.
Melzak, calls this the strategy of expanding the problem, as in linear programming
(PL, also numerical algebra).
- campanological group
. - PL "group,
campanological".
- cancellation property
. - If, for general
operation (PL) o, it is the case that x o z =
y o z iff x = y, for x, y, z elements
of an algebraic system, then the system is right-cancellative; if z o x
= z o y iff x = y, the system is left-cancellative; if
both, the system is cancellative. Significant for a system such as a group (PL) with
group operations such as +, *. This property may hold in a ring
with no division operations, such as an integral domain (PL). The term "cancellative"
also denotes dividing equivalent (non-zero) factors out of the numerator, denominator (PL)
of a fraction (PL), such as ac/bc = a/b for nonzero b, c. (This property denotes well-definedness (PL) of subtraction,
division.)
- canonical basis
. - Basis (PL) {e1, e2, ..., en} of Rn,
as vector space over the real numbers R, with
ei the column/row vector (PL) having 1 in ith
position and 0 elsewhere.
- canonical partition of factorial
. - PL
partial.
- canonical transformation
. - Any
transformation of the coordinates on a symplectic manifold (PL) leavING the canonical 2-forms (PL)
in invariant form. Such a coordinate change also leaves Hamilton's equations (PL)
unchanged. Also, any function or transformation that has a standard form in some context.
- Cantor diagonal process
. - Pl diagonal
process.
- Cantor's paradox
. - (1) The set of
all sets is its own power set. (2) The cardinality of the powerset of a set is greater
than the cardinality of a set. (3)Therefore, the set of all sets has a greater cardinality
than itself. Paradox is avoided by cautionary language.
- cap
. - PL spherical cap.
- capacity
. - PL transfinite diameter
or Robin's constant.
- capacity dimension
. - Nonintegral
dimension for a fractal whose capacity is different from its topological dilmension (PL). The
capacity of a compact metric space is a real number (PL),
dcapacity, s. t., if n(e) is
proportional to e-D as e
 0. Formally,
dcapacity
0. Formally,
dcapacity  - lime
- lime 0+(ln N)/(ln e) (if the limit exists), for N the number of elements forming a finite cover (PL) of the appropriate metric
space, with e a bound on the diameter of the involved sets.
If elements of a fractal are equally visited, dcapacity = d
information, where the latter is the information dimension. Result:
dcorrelation
0+(ln N)/(ln e) (if the limit exists), for N the number of elements forming a finite cover (PL) of the appropriate metric
space, with e a bound on the diameter of the involved sets.
If elements of a fractal are equally visited, dcapacity = d
information, where the latter is the information dimension. Result:
dcorrelation  dinformation
dinformation
 dcapacity, where the correlation dimension is
conjectured to be equal to the trapdoor dimension (PL) .
dcapacity, where the correlation dimension is
conjectured to be equal to the trapdoor dimension (PL) .
- cap product
. - Denotes operation of
intersection (PL) in set theory, symbolized
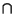 .
.
- cardinal number
. - The cardinal
number c is the equivalence class (PL) of
all collections mutually in one-one correspondence. (PL) also ordinal number
and the paradox of counting.) Children can easily be taught cardinality by a
brown bag model.
- cardioid
. - Curve described by (x2 + y2 - ax)2 = a2(x2 + y2
). A degenerate case of the limaçon.
- carry
. - The process in arithmetic
addition (PL) arising when the sum of the digits in a given notational position
is cb + d, with b the number base, d < b, and c > 0; then d
is entered in the given position of the sum, and c is carried
or added to the next-higher-order digit.
- Cartan-Diedonné theorem
. - Every
orthgonal (PL) transformation (PL) can be formulated as the composite (PL) of at
most n reflections.
- Cartan matrix
. - A square positive
definite matrix with 2 along diagonal, with nonpositive
numbers off-diagonal, and zeroed symmetrically. Given another square matrix,
its conjugate (PL) is a symmetric positive definite quadratic form. Associated
with a Lie semisimple algebra (PL).
- Cartesian axis
. - One of the x, y, z axes in Euclidean space. In general, any of a set of n
 2 mutually perpendicular lines intersecting at a single point,
called the origin.
2 mutually perpendicular lines intersecting at a single point,
called the origin.
- Cartesian coordinates
. - PL Cartesian
coordinate system.
- Cartesian coordinate system
. - In n-space, the coordinate system represented by n
Cartesian axes. Also labeled rectangular coordinates.
- Cartesian ovals
. - Studied by Descartes
in 1637: the locus of point P whose distances from two foci
, F1, F2 (in 2-center bipolar coordinates)
is given by mr ± nr' = k, for positive integers,
m, n; positive real k; and
F1,
F2. For m = n, the oval becomes an ellipse.
- Cartesian product
. - Given two sets,
A, B, their Cartesian product, A x b, is
the set of all ordered pairs or 2-tuples with first component from set, A and second component from set, B. (Sometimes used
to describe multiplication in arithmetic.) Various applications. For example, in
topology, a cylinder (PL) is the Cartesian product, C X L
, where C denotes the set of points in a circle and L denotes the set of points in a line segment. One topological
structure which cannot be factored into a Cartesian product is the Möboid
(PL).
- Cartesian surface
. - A
surface in 3-D space created by rotating the curve b
0(x2 + y2) 1/2 ± b1
[(x - a)2 + y2]1/2 = c about the x-axis.
- Cartesian tensor
. - A tnesor (PL)
transformation from one rectangular coordinate system (PL) to another.
- casting out elevens
. - An
algorithm providing a check on arithmetic computations, based on the
result that the residue (remainder) of an integer (
mod 11: modulus (PL) eleven) equals the residue (mod 11) of the alternating sum (PL) of the digits of the
integer. (Example: given 176, the right-to-left alternating sum
is 6 - 7 + 1 = 0, hence, this number is a multiple of 11: 176 = 11 * 16.) For a method of teaching this to children, PL casting out
nines. Also, PL casting out x's.
- casting out nines
. - An
algorithm (PL) providing a check on arithmetic computations, based on
the result that the residue (remainder) of an integer (mod 9: modulus (PL) nine) equals the residue (mod 9) of the sum of the digits of the integer. (Given
144, the right-to-left sum is 4 + 4 + 1 = 9, and 9 (mod 9) = 0, so the number is a multiple of nine: 144 = 9 *
16. PL casting out elevens.) This is the basis of an accountancy "trick": bookkeeper's
check. (Children can learn "casting out nines" and "casting out elevens" from a mathtivity.) Also, PL casting out
x's.
- casting out powers of five
. - We
use a ten as a base (PL) and five is a prime factor (PL) of ten. Hence, we
have an algorithm for detecting a power of two as factor of a number in terms
of certain last digits of the number. The (decimally written) number n has a factor 5p iff the last
p digits of number n forms a
multiple of 5p. (Thus, 51
= 5 is a factor iff the last digit is a multiple of five, namely, zero or
five. Then, 52 = 25 is a factor iff the last two
digits forms a multiple of twenty-five. Again, 53 = 125
is a factor iff the last three digits forms a multiple of one-hundred-twenty-five.
Etc. (Children can learn this by studying a "mathtivity" about powers of five.)
- casting out powers of two
. - We use a
ten as a base (PL) and two is a prime factor (PL) of ten. Hence, we have an
algorithm for detecting a power of two as factor of a number in terms of certain
last digits of the number, The (decimally written) number n
has a factor 2p iff the last p digits of number n forms a multiple of
2p. (Thus, 21 = 2
is a factor iff the last digit is a multiple of two, namely, zero, two, four, six, eight.
Then, 22 = 4 is a factor iff the last two digits forms
a multiple of four. Again, 23 = 8 is a factor iff the
last three digits forms a multiple of eight. Etc. (Children can learn this by studying a
"mathtivity" about powers of two.)
- casting out sevens
. - The algorithm
of casting out nines or elevens derives from (1) the condition that testing any
decimally notated number that is a multiple of nine or eleven, when tested
mod 9 or mod 11, equals zero; (2) the patterns of nines
and elevens (PL) are obvvious diagonal or codiagonal patterns. However, while the first condition
follows for mod 7 or modulus any other number, yet nothing so
simple as condition (2) follows for seven, etc. This is easily confirmed by seeing how
seven-multiples jump around in a tens-grid.
Hence, it is easier simply to test a number by dividing it by seven. Similarly, for other numbers.
- casting out x's
. - Just as ten is
the number base (PL) we commonly use ("decimal system"), so x
acts as a base for algebraic equations. And, just as "neighbors" ten, eleven
of this base have casting out algorithms for the "neighbors" of x,
namely, x - 1, x + 1: (1) iff the sum of the coefficients of the
algebraic equation equals zero, then the equation has a factor x - 1;
(2) iff the alternating sum (PL) of the coefficients of the algebraic equation equals zero,
then the equation has a factor x + 1. (Example: given
5x5 - 4x4 + 2x3 + 2x2 -7x + 2 = 0, the right-to-left
sum is 2 - 7 + 2 + 2 - 4 + 5 = 0, so the equation has factor
x - 1; the right-to-left alternating sum is 2 + 7
+ 2 - 2 - 4 - 5 = 0, so that the equation has factor x + 1; hence, it
has the factor (x - 1)(x + 1) = (x2 - 1); checking,
5x5 - 4x4 +2x3 + 2x2 -7x + 2 = (x2 - 1)(5x3
- 4x2 + 7x - 2).)
- Catalan number
- Created by Eugene
Charles Catalan (1813-1894), these numbers form an integer sequence Cn
which appears in tree (PL) enumeration problems such as, "In how many ways can a
regular n-gon be divided into triangles if different orientations are
counted separately?", e.g., Euler's polygon division problem (PL). The solution is the
Catalan number C(n - 2). Equivalently, the nth Catalan number,
Cn = (1/n)C(2n-2,n-1) = (1/n)(2n-2)!/(n-1)!(n-1)! enumerates the number of
monotonically sequenced paths from lattice points (PL) (1,0) to
(n,n-1); the number of ways a polygon with n +
2 sides can be cut into n triangles; the number of
ways in which parentheses can be placed in a sequence of numbers to be multiplied, two at a time;
the number of rooted, trivalent trees with >n + 1 nodes; and the
number of paths of length 2n through an n X n
grid that do not rise above the main diagonal. The first few Catalan numbers
for n = 1, 2, ... are 1, 2, 5, 14, 42, 132, 429,
1430, 4862, 16796, ....
- catastrophe
- In minimizing one of an
equational system, only seven types of catastrophe (PL) are standard, given four or
fewer functands (PL): (1) fold, with one control factor (PL) and one
behavior axis (PL), the unfolding of singularity x3
in x3 + ux; (2) cusp, for two control
factors and one behavior axis, the universal unfolding of singlarity 4 in x4 + ux2 + vx, and
y = x3/2 also has cusp c.; (3) swallowtail,
with three control factors and one behavior axis, the universal unfolding of
x5 for codimension three (three unfolding parameters), in equation x
5 + ux3 + vx2 + wx; (4) butterfly, with four control
factors and one behavior axis for codimension four, the universal unfolding of
x6 in equation x6 + ux4
+ vx3 + vx2 + tx; (5) elliptic umbilic, with three
control factors and two behavior axes of codimension three, in equation
x3/3 - xy2 + w(x2 + y2) -ux - vy; (6)
hyperbolic umbilic, with three control factors and two behavior axes of codimension three,
the universal unfolding of function germ (PL), x3 + y3
; (7) parabolic umbilic, with four control factors and 2 behavior axes, thr
unfolding of y4 + x2y + ux2 + vy2
+ wx + ty in equation x4 + ux + vx. (PL
umbilic point.)
- catastrophe theory
- Study of how
qualitative nature of equational solutions depends on equational parameters (PL).
(Subsumes bifurcation theory, nonequilibrium thermodynamics, singularity theory
, synergetics, topological dynamics -- PL.) In minimizing one of an
equational system, only seven types of catastrophe (PL) are standard, given four or
fewer functands (PL).
- category
. - A collection of objects
(groups>, vector spaces, differentiable manifolds, etc.) s.t., for any pair
of objects, there is a collection of MORPHISMS (PL) from one object to another.
- category theory
. - PL category.
- catenary
. - The graph of the equation y = a cosh(x/a). This plane curve (PL), under force of gravity (the
y -direction), in which a uniform flexible cable hangs when suspended
from two points, where a > 0 is the y
-intercept. (We see the catenary curve in drapes hanging from a rod, or in suspension
chains of a large bridge.)
- catenoid
. - A catenary (PL) of
revolution. (The catenoid and plane are the only surfaces of revolution which are also
minmal surfaces.) Given by the parametric equations: x = c cosh (v/c)
cos u, Y = c cosh (v/c) sin u, Z = V.
- Cauchy problem
. - Given an analytic
function (PL), f(x, y), in a neighborhood (PL) of a point,
(x0, y0) to find a solution of the differential
equation, Dxy = f(x), with initial conditions,
x = x0, y = y0.
- Cauchy residue theorem
. - Obviously, the
plane has no "holes". So encircling a region of it by a closed curve encloses no holes. And if
the plane is the complex plane and the curve is generated by a complex function
without any singularity (equivalent to 1/0), the situation is the same. A contour
integral for the latter region is zero, since the summation of one part cancels out that for
the remaining part. However, if the region has any simple singularity or pole (PL), a
nonnegative residue measure renders the total measure postive. Cauchy showed that this
residue can be completely described by the coefficient of the first term, say,
a-1, in "the principal part" of the Laurent series (PL,
complex "Taylor series") for this singularity. In general, for poles, a, b, c, d, ..., n, for contour g,
the residue summation is
 gf(z) = S
ak Res(f(z)) = (2ip(a-1 + b-1 +
c-1 + d-1 + ... + n-1).
gf(z) = S
ak Res(f(z)) = (2ip(a-1 + b-1 +
c-1 + d-1 + ... + n-1).
Cauchy-Riemann equations.
The necessary and sufficient conditions for a complex function,
f(z) = u(x,y) + iv(x,y) to be analytic (PL) in a region. Given
reals, a, b, c, d, equality of the complex numbers
(PL), a+ib = c+id is that a = c, b = d. For the
two writings of the derivative of f(z) (above), this equality requires:
Dx(u) = Dy(v) and Dy
(u) = - Dx(v), the Cauchy-Riemann equations.
Cauchy sequence.
A sequence {an} such that, for every e > 0, there is an integer N
whereby |an - am| < e
for all m, n > N. PL real number system.
caustic. Image of a Lagrangian submanifold
of the cotangent bundle of a manifold M in which the projection onto
M has become singular.
Cayley algebra PL octonion.
Cayley-Hamilton theorem. Since the
positive power of a matrix (PL) can be defined, the polynomial functions
of matrices can be constructed, using the identity matrix, I
(PL): f(M) = Mn + a1M n-1 + ... + an - 1
M + I = 0. All operations of polynomial arithmetic (subject to compatible matrix
multiplication) can be performed thereby.
Cayley-Klein parameters. For 3-D rotation,
in terms of the Euler angles (PL), q, f, y, these parameters (related to
quaternions, PL) are: a = e½i(
y + f) cos (½q
), b = e½i(y - f) sin (½q),
g = e-½i(y -
f sin (½)q, d = e-i½(y + f)
cos (½q). Given as a matrix:
æ a b ö
ç ÷
è g d ø,
this results in the transformations: u' = au
+ bv, v' = gu +
dv, of a linear space (PL) with complex axes.
However, applying eiq as a spinor
(PL) acting upon a vector provides the most efficient rotation operator.
Cayley numbers. (1)The eight elements
in an octonion (PL) or Cayley algebra (PL). (2) An element describing a Del
Pezzo surface.
Cayley's sextic. A curve
discovered by Colin MacLaurin (1698-1746), studied in detail by Cayley. r =
4a cos3(½q).
Cayley table. The multiplication
(concatenation) table of a given group whereby the product of row (group)
element (in table) with column(group) element (concatenated order thereof) yields
the cell (group) element.
Cayley's theorem. Given a finite group, G, with order (PL) divisible by prime, p, then group G, contains an element of order p.
cell. A finite regular polytope
(PL).
ceiling fnction. Provides the least
integer greater than or equal to a given number, denoted |_
x_|. (PL floor function.)
center. A point with
symmetric position w. r. to a curve or in a solid. Example, center of a circle.
center of area. Given a 2-D
figure, the mass center of a homogeneous plate with the same boundaries as a specified
figure.
center of similitude (self-homologous point).
Given two similar (PL) figures on a plane, there is a center of similitude with
the same homologous postition w. r. to both figures. Thus, for two conconcentric circles, another
circle exists with its diameter joining their two homothetic centers.
center of volume. Given a 3-D
figure, the mass center of a solid (PL) with the same boundaries as a specified
figure.
centralizer (of group element). Given
group G with element g, the
centralizer of g is the set of all elements of the group which
commute with g: CG = {x e G: xg = gx}.
centroid. The center of mass.
Ceva's theorem. Given a triangle
with vertices (PL), A, B, C, and points D, E,
F along the sides, the n. a. s. c. that the cevians (PL) be concurrent (PL)
is that BD . CE . AF = DC . EA .
FB. (Published by Giovanni Ceva in 1678.)
cevian(s). A line joining vertex
of a triangle with a point on its opposite side (or extension thereof).
chain. (1) Nonempty linearly ordered
set or partial ordering  , on a set
C in which either x
, on a set
C in which either x  y or y
y or y  x for every
x, y in C. One chain is a refinement
of a second chain iff containing all elements of the second chain. Two chains are
said to be equivalent iff there exists a one-to-one, order-preserving correspondence
between their elements. Also, labeled a totally ordered set. A chain may consist of
numericals, lattice points (forming lattice "columns", just as antichains (PL) form its
"rows"), algebraic submodules, etc. If the linear ordering is
x for every
x, y in C. One chain is a refinement
of a second chain iff containing all elements of the second chain. Two chains are
said to be equivalent iff there exists a one-to-one, order-preserving correspondence
between their elements. Also, labeled a totally ordered set. A chain may consist of
numericals, lattice points (forming lattice "columns", just as antichains (PL) form its
"rows"), algebraic submodules, etc. If the linear ordering is  , the chain is ascending chain; if
, the chain is ascending chain; if  ,
a descending chain. (2) In integration theory, a (finite) formal sum of singular
n-cubes in Rn is an n
-chain. (PL antichain.) The integral of a 1-form over a 1-chain is a line integral; an integral
of a 2-form over a 2-chain is a surface integral. (3) The collection
{Di}, 0
,
a descending chain. (2) In integration theory, a (finite) formal sum of singular
n-cubes in Rn is an n
-chain. (PL antichain.) The integral of a 1-form over a 1-chain is a line integral; an integral
of a 2-form over a 2-chain is a surface integral. (3) The collection
{Di}, 0  i
i  n, of open
disks is a chain of disks if Di-1
n, of open
disks is a chain of disks if Di-1 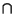 Di
Di 
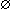 , 1
, 1  i
i  n. Used in analytic continuation. Also, circle chain.
chain complex. A sequence of
maps,
n. Used in analytic continuation. Also, circle chain.
chain complex. A sequence of
maps, 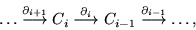 , provided that
, provided that 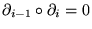 . The spaces, Ci, are
modules, Abelian groups, etc. Chain complexes define or compute homology groups
; cochain complexes for cohomology. The chain concept is critical in the
definition of a solvable group (PL).
chain condition, ascending. For
;oset (PL), condition requires all its increasing sequences eventually to become
constant. (A module satisfies the a. c. c. if all its submodules do so,
becoming Noetherian.)
chain condition, descending. The dual
of ascending chain condition, for decreasing sequences. A module which
satisfies this condition is Artinian.
chain factoring. Reduction or inverse of
a chain product (PL).
chain, prime. A chain (PL) from the
1-atom of a lattice to a prime (number) carrier.
chain product. (1)Given a collection of
prime chains (PL), form their Cartesian product (PL); (2) reduce this set to be
extollent (PL) with the cardinality of the original collection.
characters, group. The traces
(sum of diagonal terms) of those matrices of irreducible representations of
groups whereby their multiplication yields the multiplication table (PL, a.k.a. Cayley
table) of the group. All members of the same conjugacy class have the same character
. However, since other conjugacy classes may have the same characters, the abstract
group, in its character table (PL), lists all such representations. (But other
nonisomorhic groups may satisfy the same character table.)
characteristic function (probability).
f(t) is the Fourier transform (PL
) of the probability density (PL) with F. T. parameters of (a,b)
= (1, 2). A characteristic function can generate moments or cumulants
for probability distributions.
characteristic (a.k.a. proper, eigenvalue) equation(s)
. Given square matrix, M, and column matrix
of components of vector, v, expansion of matrix equation,
Mv = tv, for "unknown" ("indeterminate") t relates
to solutions of the characteristic polynomial (PL).
characteristic function (set). PL
indicator function.
characteristic polynomial. Given a
sqyare matrix, M and compatible identity matrix I, form determinant, det[M -tI], for parameter
, t. The expansion of this determinant is the characteristic
polynomial , whose roots are the characteristic values of M
. Substituion of these in the characteristic equation (PL) yields the
characteristic vectors (PL) for M.
characteristic vector(s). PL
characteristic polynomial.
chart. Points in a small neighborhood
(PL) of a manifold (PL) rendered as coordinates (PL) in Euclidean space
(PL).
cheating in arithmetic theory. In
beginning arithmetic, students are (quasi-axiomatically) taught natural number arithmetic
and told (for example), "You can't subtract three from two". Later, they are (quasi-axiomatically)
taught integer arithmetic and told, "two minus three is minus one". Apart from
the bad language of "minus one" (instead of "negative one", PL), this gives the impression that
you can transcend or violate the rules of arithmetic by putting a funny sign in front of a number
-- implicitly, this is cheating. Similarly, students are told (for example), "You cannot evenly
divide five by two". Later, they are (quasi-axiomatically) taught "fractions" and told (for example),
"Five divided by two is the fraction five-halves". Again, cheating-by-funnysigns! Is it any wonder
that so many students have "trouble with arithmetic"? (Such cheating and unnrcessary
weirdness helps to create "innumeracy" and "mathephobia", endemic in our society.)
Actually, in constructing integers as vectors of naturals and of rationals as vectors
of integers (PL), these rules are never violated, and the student can understand
the why-and-wherefore -- without cheating. (PL weirdness in arithmetic theory.)
cheating in logic. PL weirdness
in proofs.
cheating in proofs. Default logico-mathematical
proofing, when a constructive proof (PL) cannot be found, turns to proof-by-contradiction:
(1) assume the negative (contradiction) of the thesis to be proven; (2) follow the consequences of
this negation; (3) if this leads to a contradiction, then claim that the thesis is proven -- "double
negation equals positive", as with a two-pole night switch. To leave the matter with this is cheating.
(However, it could be called "second-class" logic or mathematics, since a constructive proof
teaches us much more, so is "first-class". And nonconstructive proofs sometimes motivate constructive
proofs. PL a fable on this subject. PL the axiom
of choice, the other frequently used nonconstructive proof: cheating with sometimes weird
consequences.)
Chebyshev differential equation. (1 - x3)Dxxy -xDxy - a2x = 0, with
regular singularities at -1, 1,
. The spaces, Ci, are
modules, Abelian groups, etc. Chain complexes define or compute homology groups
; cochain complexes for cohomology. The chain concept is critical in the
definition of a solvable group (PL).
chain condition, ascending. For
;oset (PL), condition requires all its increasing sequences eventually to become
constant. (A module satisfies the a. c. c. if all its submodules do so,
becoming Noetherian.)
chain condition, descending. The dual
of ascending chain condition, for decreasing sequences. A module which
satisfies this condition is Artinian.
chain factoring. Reduction or inverse of
a chain product (PL).
chain, prime. A chain (PL) from the
1-atom of a lattice to a prime (number) carrier.
chain product. (1)Given a collection of
prime chains (PL), form their Cartesian product (PL); (2) reduce this set to be
extollent (PL) with the cardinality of the original collection.
characters, group. The traces
(sum of diagonal terms) of those matrices of irreducible representations of
groups whereby their multiplication yields the multiplication table (PL, a.k.a. Cayley
table) of the group. All members of the same conjugacy class have the same character
. However, since other conjugacy classes may have the same characters, the abstract
group, in its character table (PL), lists all such representations. (But other
nonisomorhic groups may satisfy the same character table.)
characteristic function (probability).
f(t) is the Fourier transform (PL
) of the probability density (PL) with F. T. parameters of (a,b)
= (1, 2). A characteristic function can generate moments or cumulants
for probability distributions.
characteristic (a.k.a. proper, eigenvalue) equation(s)
. Given square matrix, M, and column matrix
of components of vector, v, expansion of matrix equation,
Mv = tv, for "unknown" ("indeterminate") t relates
to solutions of the characteristic polynomial (PL).
characteristic function (set). PL
indicator function.
characteristic polynomial. Given a
sqyare matrix, M and compatible identity matrix I, form determinant, det[M -tI], for parameter
, t. The expansion of this determinant is the characteristic
polynomial , whose roots are the characteristic values of M
. Substituion of these in the characteristic equation (PL) yields the
characteristic vectors (PL) for M.
characteristic vector(s). PL
characteristic polynomial.
chart. Points in a small neighborhood
(PL) of a manifold (PL) rendered as coordinates (PL) in Euclidean space
(PL).
cheating in arithmetic theory. In
beginning arithmetic, students are (quasi-axiomatically) taught natural number arithmetic
and told (for example), "You can't subtract three from two". Later, they are (quasi-axiomatically)
taught integer arithmetic and told, "two minus three is minus one". Apart from
the bad language of "minus one" (instead of "negative one", PL), this gives the impression that
you can transcend or violate the rules of arithmetic by putting a funny sign in front of a number
-- implicitly, this is cheating. Similarly, students are told (for example), "You cannot evenly
divide five by two". Later, they are (quasi-axiomatically) taught "fractions" and told (for example),
"Five divided by two is the fraction five-halves". Again, cheating-by-funnysigns! Is it any wonder
that so many students have "trouble with arithmetic"? (Such cheating and unnrcessary
weirdness helps to create "innumeracy" and "mathephobia", endemic in our society.)
Actually, in constructing integers as vectors of naturals and of rationals as vectors
of integers (PL), these rules are never violated, and the student can understand
the why-and-wherefore -- without cheating. (PL weirdness in arithmetic theory.)
cheating in logic. PL weirdness
in proofs.
cheating in proofs. Default logico-mathematical
proofing, when a constructive proof (PL) cannot be found, turns to proof-by-contradiction:
(1) assume the negative (contradiction) of the thesis to be proven; (2) follow the consequences of
this negation; (3) if this leads to a contradiction, then claim that the thesis is proven -- "double
negation equals positive", as with a two-pole night switch. To leave the matter with this is cheating.
(However, it could be called "second-class" logic or mathematics, since a constructive proof
teaches us much more, so is "first-class". And nonconstructive proofs sometimes motivate constructive
proofs. PL a fable on this subject. PL the axiom
of choice, the other frequently used nonconstructive proof: cheating with sometimes weird
consequences.)
Chebyshev differential equation. (1 - x3)Dxxy -xDxy - a2x = 0, with
regular singularities at -1, 1,  .
Chebyshev polynomial of first kind. Set
of orthogonal polynomials solving Chebyshev differential equation (PL), denoted
Tn(x). PL C. p. of second kind.
Chebyshev polynomial of second kind. Set
of orthogonal polynomials solving Chebyshev differential equation (PL), denoted Un(x). PL C. p. of first kind.
Chern class. The i
th Chern class is in the 2ith cohomology group (PL) of the
base space (PL) of the tangent bundle (PL) of a complex manifold (PL).
Chinese postman problem. Shortest tour
in a graph visiting each edge at least once. In Eulerian graph (PL), the
Eulerian circuit (PL), is optimal solution. In a tree, The tour crosses
each edge twice.
Chinese remainder theorem. For r, s two relatively prime (PL) positive integers, and for any
two integers, a, b, there exists an integer, N,
s.t. N
.
Chebyshev polynomial of first kind. Set
of orthogonal polynomials solving Chebyshev differential equation (PL), denoted
Tn(x). PL C. p. of second kind.
Chebyshev polynomial of second kind. Set
of orthogonal polynomials solving Chebyshev differential equation (PL), denoted Un(x). PL C. p. of first kind.
Chern class. The i
th Chern class is in the 2ith cohomology group (PL) of the
base space (PL) of the tangent bundle (PL) of a complex manifold (PL).
Chinese postman problem. Shortest tour
in a graph visiting each edge at least once. In Eulerian graph (PL), the
Eulerian circuit (PL), is optimal solution. In a tree, The tour crosses
each edge twice.
Chinese remainder theorem. For r, s two relatively prime (PL) positive integers, and for any
two integers, a, b, there exists an integer, N,
s.t. N  a (mod r) and N
a (mod r) and N  b (mod s), with N uniquely determine modulo
rs. Equivalently, if (r, s) = 1, then every
pair of residue classes modulo rs corresponds to a simple
residue class modulo rs.
choice function. Given
C as the collection of subsets of a given set X. A choice
function f is a function with domain C
such that, if A is in C, then
f(A) is in A. Intuitively, f
"chooses" a representative element out of each set of C. C can be considered an indexed family of sets, with C
itself as the index set whose identity mapping performs the indexing. Then
f is a choice function satisfying the requirements of the axiom of choice (PL) for the
Cartesian product (PL) of the sets of C; i.e., each such f can be regarded as an element of this generalized Cartesian product. This
argument allows such nonconstructive proofs as the Banach-Tarski Paradox.
Cholesky decomposition. An upper
triangular (PL) positive definite matrix, B (with
transpose, PL, BT), for matrix A
s.t. A = BTB.
chord. A line segment intersecting a curve
or surface only at its two endpoints. Before the development of trigonometry and trigonometric
tables, mathematicians and engineers used tables of chords. One famous table of chords was
work of Ptolemy (2nd century AD) in describing his geocentric hypthesis that the sun encircles the earth.
For use in graph theory, PL http://www.harcourt.com/dictionary /browse/19/.
chromatic number. Fewest number of
colors for coloring edges (PL) of a graph s.t. no two edges incident on
the same vertex have the same color. (A problem in combinatorics, PL.)
chromatic polynomial. Count number of
ways to color a graph(PL) with specified number of colors.
Church's thesis. Any computation
is eqivalent to a formulation in Alonzo Church's lambda calculus (PL).
Church-Turing thesis. Since any
formulation in Church's lambda calculus is equivalent to a Turing machine (PL),
Churches's thesis (PL) declares that any computation can be performed by a Turing machine.
circle. Set of points equidistant,
r (radius PL) from a center point. Twice the radius is
the diameter, d, a segment passing through the center equally
subdividing the circle. The perimeter (PL), C, of the circle
is its "circumference". The circle is the plane figure which provides the maximum area for the
minimum perimeter, a condition encapsulated in the irrational real number (PL), p = C/d.
circle of curvature. The circle most closely fitting
a curve at a given point. Thus, given point p on plane curve C, with nonzero finite curvature q at p,
the circle of curvature at p is the circle of radius 1/q
tangent to C at p on the concave side; that is,
the circle tangent to C at p that has the same curvature
as C at p. Measure 1/q is
the radius of curvature, and the center of the circle is labeled the center of curvature.
circle of inversion (inverse circle). An
inverse curve or inverse set of point can be computed with reference to this. In
3-D a sphere (PL) is used.
circuit. A cycle (PL) of a
graph (PL) which is a subset (PL) of an edge-set (PL) s.t. initial and
terminal points coincide.
circuit rank (cyclomatic number). Given
graph of N edges and n nodes
, this number, g, is the minimum of
edges and nodes removable from the graph to dissemble a circuit (PL): g = N - n + 1.
circulant matrix. A matrix (PL)
with rows (PL) composed of cyclical shifts on an n-list.
circular functions. The proper name for
trigonometric functions (PL), which seems to limit study to "measurement of
triangles".
circumcenter. for a polygon (PL)
with a circumcircle (PL) or arbitrary triangle, the circumcenter is
the center of the circumscribed circle.
circumcircle. A circumscribed
circle (PL)
circumference. Perimeter of
(distance around) a circle, equal to 2 p r
for circle radius (PL) r.
circumradius. Radius of
circumscribed circle of a regular polygon (PL) or any triangle (PL).
circumscribed. A closed curve (or
surface) is "circumscribed" about a polygon (or polyhedron) if the polygon is inside the curve
and every vertex of the polygon is on the curve. The polygon "inscribed" in the curve.
A polygon (or polyhedron) is said "circumscribed" about a closed curve (or surface) if the
curve is inside the polygon and if every edge (or face) of the polygon is tangent to the curve.
The curve is "inscribed" in the polygon.
cissoid ("ivy shaped"). Given curves
, C,D, and point, O, let line from
O cut curve C at A and
curve D at B. The locus of point P s. t. OP = AB is the cissoid.
Clairaut's differential equation. y = xDxy + f(Dxy), with solution, y = cx + f(c).
classical groups. General linear groups,
orthogonal groups, unitary groups, symplectic groups (PL). (Replace the general linear groups
with the special linear groups (PL) to form the principal series of semisimple Lie groups
(PL).)
classification theorem of surfaces. The
diversity of all such forms reduces to topological (PL) equivalence of spheres (PL) with some
number of handles (PL) or cross-caps (PL).
clifford number. These
arise from multivector theory (PL) and form an ordering
(PL) denoted by Ci,
i = 0,1,2,3,...:
b (mod s), with N uniquely determine modulo
rs. Equivalently, if (r, s) = 1, then every
pair of residue classes modulo rs corresponds to a simple
residue class modulo rs.
choice function. Given
C as the collection of subsets of a given set X. A choice
function f is a function with domain C
such that, if A is in C, then
f(A) is in A. Intuitively, f
"chooses" a representative element out of each set of C. C can be considered an indexed family of sets, with C
itself as the index set whose identity mapping performs the indexing. Then
f is a choice function satisfying the requirements of the axiom of choice (PL) for the
Cartesian product (PL) of the sets of C; i.e., each such f can be regarded as an element of this generalized Cartesian product. This
argument allows such nonconstructive proofs as the Banach-Tarski Paradox.
Cholesky decomposition. An upper
triangular (PL) positive definite matrix, B (with
transpose, PL, BT), for matrix A
s.t. A = BTB.
chord. A line segment intersecting a curve
or surface only at its two endpoints. Before the development of trigonometry and trigonometric
tables, mathematicians and engineers used tables of chords. One famous table of chords was
work of Ptolemy (2nd century AD) in describing his geocentric hypthesis that the sun encircles the earth.
For use in graph theory, PL http://www.harcourt.com/dictionary /browse/19/.
chromatic number. Fewest number of
colors for coloring edges (PL) of a graph s.t. no two edges incident on
the same vertex have the same color. (A problem in combinatorics, PL.)
chromatic polynomial. Count number of
ways to color a graph(PL) with specified number of colors.
Church's thesis. Any computation
is eqivalent to a formulation in Alonzo Church's lambda calculus (PL).
Church-Turing thesis. Since any
formulation in Church's lambda calculus is equivalent to a Turing machine (PL),
Churches's thesis (PL) declares that any computation can be performed by a Turing machine.
circle. Set of points equidistant,
r (radius PL) from a center point. Twice the radius is
the diameter, d, a segment passing through the center equally
subdividing the circle. The perimeter (PL), C, of the circle
is its "circumference". The circle is the plane figure which provides the maximum area for the
minimum perimeter, a condition encapsulated in the irrational real number (PL), p = C/d.
circle of curvature. The circle most closely fitting
a curve at a given point. Thus, given point p on plane curve C, with nonzero finite curvature q at p,
the circle of curvature at p is the circle of radius 1/q
tangent to C at p on the concave side; that is,
the circle tangent to C at p that has the same curvature
as C at p. Measure 1/q is
the radius of curvature, and the center of the circle is labeled the center of curvature.
circle of inversion (inverse circle). An
inverse curve or inverse set of point can be computed with reference to this. In
3-D a sphere (PL) is used.
circuit. A cycle (PL) of a
graph (PL) which is a subset (PL) of an edge-set (PL) s.t. initial and
terminal points coincide.
circuit rank (cyclomatic number). Given
graph of N edges and n nodes
, this number, g, is the minimum of
edges and nodes removable from the graph to dissemble a circuit (PL): g = N - n + 1.
circulant matrix. A matrix (PL)
with rows (PL) composed of cyclical shifts on an n-list.
circular functions. The proper name for
trigonometric functions (PL), which seems to limit study to "measurement of
triangles".
circumcenter. for a polygon (PL)
with a circumcircle (PL) or arbitrary triangle, the circumcenter is
the center of the circumscribed circle.
circumcircle. A circumscribed
circle (PL)
circumference. Perimeter of
(distance around) a circle, equal to 2 p r
for circle radius (PL) r.
circumradius. Radius of
circumscribed circle of a regular polygon (PL) or any triangle (PL).
circumscribed. A closed curve (or
surface) is "circumscribed" about a polygon (or polyhedron) if the polygon is inside the curve
and every vertex of the polygon is on the curve. The polygon "inscribed" in the curve.
A polygon (or polyhedron) is said "circumscribed" about a closed curve (or surface) if the
curve is inside the polygon and if every edge (or face) of the polygon is tangent to the curve.
The curve is "inscribed" in the polygon.
cissoid ("ivy shaped"). Given curves
, C,D, and point, O, let line from
O cut curve C at A and
curve D at B. The locus of point P s. t. OP = AB is the cissoid.
Clairaut's differential equation. y = xDxy + f(Dxy), with solution, y = cx + f(c).
classical groups. General linear groups,
orthogonal groups, unitary groups, symplectic groups (PL). (Replace the general linear groups
with the special linear groups (PL) to form the principal series of semisimple Lie groups
(PL).)
classification theorem of surfaces. The
diversity of all such forms reduces to topological (PL) equivalence of spheres (PL) with some
number of handles (PL) or cross-caps (PL).
clifford number. These
arise from multivector theory (PL) and form an ordering
(PL) denoted by Ci,
i = 0,1,2,3,...:- C0 denotes the
rational number system (PL);
- C1
denotes the real number system (PL);
-
C2 denotes the complex number system (PL);
- C4 denotes the quaternion number
system (PL);
- C8 denotes
the octonion number system (PL);
etc. Each clifford number
of order C2n, for n > 0
is a spinor (PL). (Thus, complex numbers constitute the simplest
form of spinor.)
clopen. A clopen set is both closed
and open, serving as a closed or open base for a typology (PL). Any complement of a
lattice (PL) is clopen.
closed. A structure,
S, is closed for operation, O, if, whenever a, b e S, so is O(a, b). A
geometric figure and its boundary are closed.
closed ball. PL closed.
closed curve. Any curve with coincident endpoints.
closed form. A differential form W on a manifold M is closed iff its
exterior derivative is zero: d(W) = 0.
closed interval. An interval and
its end-points.
closed map. A function between two topological spaces
mapping closed sets to closed sets.
closed operator. When its result is of
the same type as its operand.
closure. The closure of a structure
means that an operation of the structure combines elements of a given type into an element of
the same type. Equivalently, given two or more gnomons(basic units, PL) of the same
kind or type, their combination is a gnomon of the same type, a means of
building a given pattern. (It's "all in the family".) A closure is the conservation of some
property. Critical in measurement.
cluster. Given a point lattice
(PL), a cluster is a collection of filled cells (PL) all connected to their
neighbors, vertically or horizontally.
clusion. An inclusion-exclusion
process.
clusion algorithm. Encompassing a set by
including one-terms, two-terms, etc., excluding the overlaps. Thus, the number
of elements in a set with two attributes, A, B: n
(A 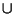 B) = n(A) + n(B) - n(A
B) = n(A) + n(B) - n(A 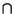 B). PL
sieving as clusion.
coaug. PL aug.
coaxial circles. Share a radical line
within a given circle.
cobordism. Pl bordant.
coboundary operator. Each MU of
a cochain complex (PL) is a coboundary.
cochain complex. PL chain complex.
cochleoid. A "snail-form" curve": (x2 + y2) tan-1(y/x) = ay.
cocycle. In cohomology (PL), the
dual of a cycle in homology.
codimension. Difference between the
dimesnion of an object and that of an object contained within it.
codomain. A set within which the values
of a function lie (as opposed to the range: set of values the function actually takes).
coefficient. A multiplicative factor
, such as ci in the polynomial:
cnxn + cn-1xn-1 + ... + c1xn +
c0.
cofactor. Signed value of a minor
of a matrix used in computing its determinant.
cognitive disssonance in mathematical language
. Mathematicians commit or allow "the cardinal sin". After honing their symbolic
language to achieve one-one effect as much as possible, their labels too often
have one-many reference with most of the referents being irrelevant or contradictory
nonmathematical ones. The effect may be comparable to hammering a fist on the piano keys,
so many tones vibrating together. With the present state of art (at this 2002 writing) for
brain scanning, it should be possible to show this. Select several univalent labels
and see the brain-scanned effect. See the effect of constructed one-many references. See
the effect of many mathematical labels and compare. PL iatrogenics.
cohomology. An invariant of a
topological space. A dual of homology, used to detect "holes" in space. Allows
a graded ring, whereas homology allows only a graded Abelian group ("part'
of a ring).
cokernel. The dual of kernel
(PL). The cokernel of a group homomorphism (PL), f: A -> B
, of an Abelian group (module, vector space, PL) is the quotient
group (PL) (quoTient module, quotient vector space, resp., PL) B /Image(f).
collinear. Said of three or more
points iff they lie on the same straight line.
collinear vectors. PL collinear.
collineation. A transformation
(PL) sending collinear points into collinear points (PL collinear.)
cologarithm. Additive inverse of
logarithm (PL). If log x = y, colog x = -y = 1/x.
coloring. The assigniing of
label or coloring or other coding to vertices (PL) or edges or
other structural parts of a graph, often invoking a formula or algoirthm
in combinatorics (PL) regarding the number of ways this can be done.
column. A matrix (PL), M
B). PL
sieving as clusion.
coaug. PL aug.
coaxial circles. Share a radical line
within a given circle.
cobordism. Pl bordant.
coboundary operator. Each MU of
a cochain complex (PL) is a coboundary.
cochain complex. PL chain complex.
cochleoid. A "snail-form" curve": (x2 + y2) tan-1(y/x) = ay.
cocycle. In cohomology (PL), the
dual of a cycle in homology.
codimension. Difference between the
dimesnion of an object and that of an object contained within it.
codomain. A set within which the values
of a function lie (as opposed to the range: set of values the function actually takes).
coefficient. A multiplicative factor
, such as ci in the polynomial:
cnxn + cn-1xn-1 + ... + c1xn +
c0.
cofactor. Signed value of a minor
of a matrix used in computing its determinant.
cognitive disssonance in mathematical language
. Mathematicians commit or allow "the cardinal sin". After honing their symbolic
language to achieve one-one effect as much as possible, their labels too often
have one-many reference with most of the referents being irrelevant or contradictory
nonmathematical ones. The effect may be comparable to hammering a fist on the piano keys,
so many tones vibrating together. With the present state of art (at this 2002 writing) for
brain scanning, it should be possible to show this. Select several univalent labels
and see the brain-scanned effect. See the effect of constructed one-many references. See
the effect of many mathematical labels and compare. PL iatrogenics.
cohomology. An invariant of a
topological space. A dual of homology, used to detect "holes" in space. Allows
a graded ring, whereas homology allows only a graded Abelian group ("part'
of a ring).
cokernel. The dual of kernel
(PL). The cokernel of a group homomorphism (PL), f: A -> B
, of an Abelian group (module, vector space, PL) is the quotient
group (PL) (quoTient module, quotient vector space, resp., PL) B /Image(f).
collinear. Said of three or more
points iff they lie on the same straight line.
collinear vectors. PL collinear.
collineation. A transformation
(PL) sending collinear points into collinear points (PL collinear.)
cologarithm. Additive inverse of
logarithm (PL). If log x = y, colog x = -y = 1/x.
coloring. The assigniing of
label or coloring or other coding to vertices (PL) or edges or
other structural parts of a graph, often invoking a formula or algoirthm
in combinatorics (PL) regarding the number of ways this can be done.
column. A matrix (PL), M  Mij
Mij  Mrc, has
i = r number of rows (PL) and j =
c number of columns.
column operations. PL elementary
matrix operations.
column space. The vector space
(PL) generated by any column (PL) of a matrix (PL) when treated as a
vector (PL).
column vector. A matrix (PL)
Mrc (PL column) for c = 1;
oftens used as right operand (PL) in matrix multiplication (PL).
combinatorial analysis. Applying
analysis (PL) (example: generating functions, (PL) to combinatoric (PL)
problems.
combinatorial topology. A special
typeof algebraic topology (PL) using methods from combinatorics (PL). For example, \
simplicial homology (PL) uses cimbinatorica construction in algebraic topology, so belongs
to combinatorial topology.
combinatoric dual graph. PL dual
graph.
combinatorics. Branch of discrete
mathematics (PL) dealing with existence, enumeration, arragngements of sets.
commensurable. Spoken of continuants,
such, line segments, whose ratio is a rational number (PL). Least common multiple (LCM, PL)
and greatest common divisor (GCD, PL) apply to commensurables.
common denominator. Any common multiple
of denominators of two or more rationals (fractions).
common fraction. Ratio of integers.
common logarithm. Logarithm to base ten.
common multiple. Number divisble by two
or more numbers.
commurand law. PL commutative
law.
commurator law The following is known in
standard arithmetic texts and articles as "the distributive law": for operands a, b, c, a*(b + c) = a*b + a* c. This label goes back to Aristotle's logic
and is misleading. It has persisted down to our time because of the medial
placement of operator signs, convenient in printing. A more revealing name is
commurator law (commutativity of operators or rators), as can be seen by
rewriting it in (Polish) prefix notation: a*(b + c)
-> *a,+b,c; a*b + a*c -> +*a,b,*a,c.
Hence, a*(b + c) = a*b + a*c -> *a,+b,c =
+*a,b,*a,c. This shows that the operators of addition and
multiplication interchange or commute, whereas it is the operands
which interchange or commute in the standard commutative laws of addition
or multiplication. (PL commurand law: commutativity of operands or rands.)
commutative law. Given any binary
operation o, and numbers a, b, their
commutation under the given operator is: a o b = b o a. A
more revealing label for this general law is commurand law in contrast
with a commurator law (PL both terms).
commutative law of addition Given numbers,
a, b: a + b = b + a. A better label is
additive communrand law (PL),
commutative law of multiplication Given
numbers, a, b: a * b = b * a. A better label is
additive communrator law (PL).
commutativity in arithmetic. This
prevails when two elements of a mathematical system interchange. In the traditional
presentation of arithmetic, in the commutative law of addition or multiplication, the
operands interchange: a + b = b + a, a * b = b * a, so for a
better label PL commurand law. And, for a better label for the "the distributive law"
PL commurator law. These involve commuting of operand or of operator.
A third distinction, in associativity of addition and multiplication, involves order of
computability of operators. This can be revealed, in general, by color coding: Oa,Ob,
c = Oa,b,O
c. On the left, the "blue" binary operator has no second
operand available until the "green" operator computes that second operand. But,
on the right, the "green" operator does not have a first operand available until the
"blue" operator computes that first operand. Thus, the order of computing
is (first on left): OO =
OO -- "green blue equals blue green" -- another variation on
commutativity. Hence, "all three law-types of arithmetic" are variations on
commutativity. One can then rescue from obscurity the connection with permutation
(literally synonymous with commutativity) which gives rise to the group structure
of which every finite group is a subgroup.
commutativity in group theory. The
property of commutativity plays a crucial role in group theory (PL). Given a
group, G, with element, g, and a
subgroup (PL), H, the right coset (PL) of G is gH = {x| x = gh, h in H}; and left coset
(PL) of G is Hg = {x| x = hg, h in H}. Then
H is a normal subgroup (PL) of G iff,
exceptionally, gH = Hg (commutativity!).
commutative diagram. Diagram(s) for a
collection of maps, fi: Ai
->Bi s.t. all maps from A to set B map in reverse.
commutative ring. A ring (PL) in
which all operators commute.
commutator. This began with the use of
the determinant in solving simultaneous algebraically linear equations -- perhaps
in the work of a 12th century Chinese mathematician. It was apparently the French mathematician,
A. L. Cauchy (1789-1857), who introduced the n x n-array as the
determinantal form. Then the British mathematician, Arthur Cayley (1821-1895), generalized
this to an array of arbitrary number of rows and columns, known as a "matrix", adopting as
the multiplicative rule for matrices the operation correct for determinants. It was
then observed that the matrix product, M * N, exists iff M has columnar number equal to the row number of N
; furthermore, when existent, this product is not, in general, commutative. To cope
with this, the bracket form commutator was introduced: [M, N] = M*N -
N*M. This form attained extensive use in mathematical physics via the Poisson bracket
of analytical mechanics and the Dirac bracket of quantum mathematics. For an
extension of this commutator, PL hays bracket.
commutator, Hays. PL Hays bracket.
commutator, group. For elements
a,b in group (PL) G, C is a commutator in G
iff c (= a-1b-1ab) -> ab=bac.
In the commutative case, c = 1.
commutator subgroup. The subgroup generated
by all commutators of a given group. The commutator subgroup of an Abelian group consists of
the identity element. If the commutator subgroup is the entire group, the group is said to
be perfect.
compactification. The compactification
of topological space, X, is another t. s.
Y which contains X s.t. Y is also
compact (PL).
compact-open topology. A common
topology (PL) for funCtion spaces (PL). Given topological spaces, X, Y, with C(X, Y) the set of continuous maps: f: X -> Y. The c.-o. t. on C(X, Y) is generated
by subsets which are compact (PL) on X and open in
C(X, Y)Y.
compact operator. Any c. o. T: V -: W is the limit of a sequence of operator,
Ti whose image (PL) is a finite-dimensional space on Mij
with Sii <
Mrc, has
i = r number of rows (PL) and j =
c number of columns.
column operations. PL elementary
matrix operations.
column space. The vector space
(PL) generated by any column (PL) of a matrix (PL) when treated as a
vector (PL).
column vector. A matrix (PL)
Mrc (PL column) for c = 1;
oftens used as right operand (PL) in matrix multiplication (PL).
combinatorial analysis. Applying
analysis (PL) (example: generating functions, (PL) to combinatoric (PL)
problems.
combinatorial topology. A special
typeof algebraic topology (PL) using methods from combinatorics (PL). For example, \
simplicial homology (PL) uses cimbinatorica construction in algebraic topology, so belongs
to combinatorial topology.
combinatoric dual graph. PL dual
graph.
combinatorics. Branch of discrete
mathematics (PL) dealing with existence, enumeration, arragngements of sets.
commensurable. Spoken of continuants,
such, line segments, whose ratio is a rational number (PL). Least common multiple (LCM, PL)
and greatest common divisor (GCD, PL) apply to commensurables.
common denominator. Any common multiple
of denominators of two or more rationals (fractions).
common fraction. Ratio of integers.
common logarithm. Logarithm to base ten.
common multiple. Number divisble by two
or more numbers.
commurand law. PL commutative
law.
commurator law The following is known in
standard arithmetic texts and articles as "the distributive law": for operands a, b, c, a*(b + c) = a*b + a* c. This label goes back to Aristotle's logic
and is misleading. It has persisted down to our time because of the medial
placement of operator signs, convenient in printing. A more revealing name is
commurator law (commutativity of operators or rators), as can be seen by
rewriting it in (Polish) prefix notation: a*(b + c)
-> *a,+b,c; a*b + a*c -> +*a,b,*a,c.
Hence, a*(b + c) = a*b + a*c -> *a,+b,c =
+*a,b,*a,c. This shows that the operators of addition and
multiplication interchange or commute, whereas it is the operands
which interchange or commute in the standard commutative laws of addition
or multiplication. (PL commurand law: commutativity of operands or rands.)
commutative law. Given any binary
operation o, and numbers a, b, their
commutation under the given operator is: a o b = b o a. A
more revealing label for this general law is commurand law in contrast
with a commurator law (PL both terms).
commutative law of addition Given numbers,
a, b: a + b = b + a. A better label is
additive communrand law (PL),
commutative law of multiplication Given
numbers, a, b: a * b = b * a. A better label is
additive communrator law (PL).
commutativity in arithmetic. This
prevails when two elements of a mathematical system interchange. In the traditional
presentation of arithmetic, in the commutative law of addition or multiplication, the
operands interchange: a + b = b + a, a * b = b * a, so for a
better label PL commurand law. And, for a better label for the "the distributive law"
PL commurator law. These involve commuting of operand or of operator.
A third distinction, in associativity of addition and multiplication, involves order of
computability of operators. This can be revealed, in general, by color coding: Oa,Ob,
c = Oa,b,O
c. On the left, the "blue" binary operator has no second
operand available until the "green" operator computes that second operand. But,
on the right, the "green" operator does not have a first operand available until the
"blue" operator computes that first operand. Thus, the order of computing
is (first on left): OO =
OO -- "green blue equals blue green" -- another variation on
commutativity. Hence, "all three law-types of arithmetic" are variations on
commutativity. One can then rescue from obscurity the connection with permutation
(literally synonymous with commutativity) which gives rise to the group structure
of which every finite group is a subgroup.
commutativity in group theory. The
property of commutativity plays a crucial role in group theory (PL). Given a
group, G, with element, g, and a
subgroup (PL), H, the right coset (PL) of G is gH = {x| x = gh, h in H}; and left coset
(PL) of G is Hg = {x| x = hg, h in H}. Then
H is a normal subgroup (PL) of G iff,
exceptionally, gH = Hg (commutativity!).
commutative diagram. Diagram(s) for a
collection of maps, fi: Ai
->Bi s.t. all maps from A to set B map in reverse.
commutative ring. A ring (PL) in
which all operators commute.
commutator. This began with the use of
the determinant in solving simultaneous algebraically linear equations -- perhaps
in the work of a 12th century Chinese mathematician. It was apparently the French mathematician,
A. L. Cauchy (1789-1857), who introduced the n x n-array as the
determinantal form. Then the British mathematician, Arthur Cayley (1821-1895), generalized
this to an array of arbitrary number of rows and columns, known as a "matrix", adopting as
the multiplicative rule for matrices the operation correct for determinants. It was
then observed that the matrix product, M * N, exists iff M has columnar number equal to the row number of N
; furthermore, when existent, this product is not, in general, commutative. To cope
with this, the bracket form commutator was introduced: [M, N] = M*N -
N*M. This form attained extensive use in mathematical physics via the Poisson bracket
of analytical mechanics and the Dirac bracket of quantum mathematics. For an
extension of this commutator, PL hays bracket.
commutator, Hays. PL Hays bracket.
commutator, group. For elements
a,b in group (PL) G, C is a commutator in G
iff c (= a-1b-1ab) -> ab=bac.
In the commutative case, c = 1.
commutator subgroup. The subgroup generated
by all commutators of a given group. The commutator subgroup of an Abelian group consists of
the identity element. If the commutator subgroup is the entire group, the group is said to
be perfect.
compactification. The compactification
of topological space, X, is another t. s.
Y which contains X s.t. Y is also
compact (PL).
compact-open topology. A common
topology (PL) for funCtion spaces (PL). Given topological spaces, X, Y, with C(X, Y) the set of continuous maps: f: X -> Y. The c.-o. t. on C(X, Y) is generated
by subsets which are compact (PL) on X and open in
C(X, Y)Y.
compact operator. Any c. o. T: V -: W is the limit of a sequence of operator,
Ti whose image (PL) is a finite-dimensional space on Mij
with Sii <  .
compact set. A set which is both
closed and bounded.
compact space. A topological space
(PL) s.t. every open cover (PL) has a finite subcover.
comparable. Two elements x, y of an ordering are comparable iff one is proper successor (PL)
of the other. (PL incomparable.)
compass. A drawing and measuring instrument
for constructing all points at a given distance from a fixed point.
complementary angle. Either of a pair of angles
summing to 90 °.
complementation. Replacement of an
element by its complement (PL).
complemented lattice. A lattice
(PL) in which every element has a complement (PL), equivalently, a partially ordered set (poset,
PL) such that every pair of elements has a join (least upper bound, a.k.a. supremum) and
a meet (greatest lower bound, a.k.a. infimum, PL).
complete bipartite graph. A bipartite
graph (PL) which is a complete greaph (PL).
complete graph. Each pair of vertices
is connected by an edge (PL). A c. g. with n
verices is denoted Kv and has C(v, 2)
edges, where C(n, k) denotes a binomial coefficient (PL).
(in older literature, a c. g. is labeled "a universal graph".) The number of vertices in
Kv is v(v - 1)/2 (the triangular
numbers, PL); and its topological genus, PL is (v - 3)(v - 4)/12,
3
.
compact set. A set which is both
closed and bounded.
compact space. A topological space
(PL) s.t. every open cover (PL) has a finite subcover.
comparable. Two elements x, y of an ordering are comparable iff one is proper successor (PL)
of the other. (PL incomparable.)
compass. A drawing and measuring instrument
for constructing all points at a given distance from a fixed point.
complementary angle. Either of a pair of angles
summing to 90 °.
complementation. Replacement of an
element by its complement (PL).
complemented lattice. A lattice
(PL) in which every element has a complement (PL), equivalently, a partially ordered set (poset,
PL) such that every pair of elements has a join (least upper bound, a.k.a. supremum) and
a meet (greatest lower bound, a.k.a. infimum, PL).
complete bipartite graph. A bipartite
graph (PL) which is a complete greaph (PL).
complete graph. Each pair of vertices
is connected by an edge (PL). A c. g. with n
verices is denoted Kv and has C(v, 2)
edges, where C(n, k) denotes a binomial coefficient (PL).
(in older literature, a c. g. is labeled "a universal graph".) The number of vertices in
Kv is v(v - 1)/2 (the triangular
numbers, PL); and its topological genus, PL is (v - 3)(v - 4)/12,
3  v.
complete integral. A solution of an
nth degree ordinary differential equation (PL) in one functand
(PL) depending on n parameters (PL) as well as the
independent functand. Also labeled complete primitive.
complete lattice. A partially ordered
set (poset (PL), possibly of unlimited extension, such that every pair of
elements has a join (least upper bound, a.k.a. supremum) and a meet
(greatest lower bound, a.k.a. infimum, PL). A complemented lattice (PL)
is a special case.
completely regular space. A
topological space, X, s. t., for every closed subset, C, of X and every point, x
e C\X, there is a continuous function,
f: X -> [0, 1], s.t. f(x) = 0 and f(C) = 1
.
complete metric space. A metric space
in which every Cauchy sequence (PL) is convergent (PL). PL completion of
a metric space.
completing the square. Converting the
quadratic polynomial, ax2 + bx + c to a(x + b/2a)2 + (c - b2/4a). Setting B
v.
complete integral. A solution of an
nth degree ordinary differential equation (PL) in one functand
(PL) depending on n parameters (PL) as well as the
independent functand. Also labeled complete primitive.
complete lattice. A partially ordered
set (poset (PL), possibly of unlimited extension, such that every pair of
elements has a join (least upper bound, a.k.a. supremum) and a meet
(greatest lower bound, a.k.a. infimum, PL). A complemented lattice (PL)
is a special case.
completely regular space. A
topological space, X, s. t., for every closed subset, C, of X and every point, x
e C\X, there is a continuous function,
f: X -> [0, 1], s.t. f(x) = 0 and f(C) = 1
.
complete metric space. A metric space
in which every Cauchy sequence (PL) is convergent (PL). PL completion of
a metric space.
completing the square. Converting the
quadratic polynomial, ax2 + bx + c to a(x + b/2a)2 + (c - b2/4a). Setting B  b/2a and C
b/2a and C  c - b2/4a
yields a(x + B)2 + C.
completion of a metric space. An
incoplete metric space, S, has a Cauchy sequence (PL) which does
not converge (PL). The space is completed by adjoining the limits to the Cauchy
sequences. (The completion is always compoete (PL).) Thus, the completion of the
rationals is the real number system. But the completion depends on the metric. Thus,
for any prime, p, the rationals have a metric given by the
p-adic norm, so that the completion of the rationals then becomes
the set of p-adic numbers. Specifically, the completion
of a metric space, S, is the set of Cauchy sequences, and
S is isometrically contained in thi set as the constant sequences
.
complex conjugate. Given the complex
number, a + bi, for i = (-1)1/2,
its conjugate is a - bi.
complex fraction. A fraction (PL)
whose numerator, denominator (PL) are fractions.
complexification. Replacing a real
parameter or functand by one that is a complex number.
complex number. A number equivalent to
the form, a + bi, for i = (-1)1/2.
complex plane. The plane (PL) of
complex numbers (PL) as in the Argand diagram (PL).
complex unit. The complex number
z = a + bi, for i = (-1)1/2 has the
polar (PL) form, z = r cos q + sin q. When r = 1, it designates a complex
unit.
complex variable (functand). A
functand (PL) assuming complex (PL) values.
composite number. Any number that is
product of two or more prime (PL) factors. Equivalently, an integer (PL) that is
neither prime nor zero nor +1 nor -1.
composition of functions. For two
functions (or mappings) f, g, with the range (output, codomain) of
f contained in the domain (input) of g, their
composition is a new function h(x) = g[f(x>)], for all x in the domain of f. The usual notation is h = g ° f, or sometimes h = f ° g (usually with
x(f)). Function composition generally is not commutative but is
associative
composition series. A normal series
of subgroups (PL) whose factors are all simple (PL).
compound number. The sum of two or more
quantities of differing units.
computation. Calculating, especially by
numerical methods.
computational geometry. Study of
efficient algorithms for solving geometric problems, such as convex hull
(PL) of a point set and Voronoi diagram (PL).
concave function. The function, f(x) is concave on an interval (PL) iff - f(x)
is convex (PL) on this interval.
concave polygon. A polygon (PL)
such there is a segment initiating and terminating in the polygon's interior which
crosses the polygon's boundary in its extension. (PL convex polygon.)
concentric circles. Coplanar circles
with differing radii but same center.
conchoid of Nicomedes. A curve with
equation (x - a)2(x2 + y2) = b2x
2.
conditional statement. An implication (PL).
cone. A pyramid with circular
cross-section (PL). (PL conic sections.)
conic sections. In his classic work, "On
Conics", Appolonius of Perga (c. 262-190? BC) showed that the ellipse, parabola, hyperbola
can be derived as sections of a cone, hence the label, "conic sections", for these curves.
configuration. Arrangement of
geometric structures, such as points, lines, surfaces, curves.
confluent hypergeometric function. PL
hypergeometric function.
confocal. Of structures having same
focus (PL) or focii.
confocal conics. Two or more conics
with the same focii or axes of symetry, such as a system
of hyperbolas or ellipses or parabolas.
confocal conics. Conics with foci
(PL) coincident. (PL elliptical coordinates.)
conformal mapping. Preserves angles
.
congruence. The coincidence of two
geometric configurations (PL) under one or more rigid transformation (PL). A
congruence relation (PL) between numbers.
congruence relation. The relation between
two or more numbers yielding the same remainder (PL) when divided by the same divisor
or modulus> (PL).
congruent. The result of congruence (PL).
congruent matrices. Pl transformation
for congruent transformation.
congruent numbers. Two or more numbers yielding the same remainder (PL) when divided by the same
divisor or modulus (PL). PL also congruence relation.
conic. Graph (PL) of 2nd-order (PL) polynomial equation (PL) in two functands (PL), representable as
intersection of plane with a bipartite cone (PL), that is, as a conic section (PL).
conical surface. pL conical sections
.
conjugate radicals. a pair of
irrational numbers of the form a(b)1/2 + c(d)1/2
and a(b)1/2 - c(d)1/2, where
a, b, c, d are rational (PL) but (b)1/2,
(d)1/2 are not both rational. Also labeled conjugate surds.
conjugation. Taking a complex
conjugate (PL) of a number, a matrix, etc.
conjunction. Binary operation on two or
more instances of logical statement (PL) (proposition, PL) yielding a compound
statement which is true iff all component statements are true.
connected graph. With a path (PL)
from any to any other point of the graph.
connected set. Cannot be partitioned into
two nonepty subsets s. t. neither can be has points in common with closure (PL) of the
other.
connected space. Any two of its points
can be connected by a curve wholly within it.
connected surface. Surface which is a
connected space (PL).
connection. Condition on a vector
bundles providing for "differentiation" of sections, homologous to exterior
derivative of a function.
connective, logical. The connectives
of standard statement logic (PL)
are
c - b2/4a
yields a(x + B)2 + C.
completion of a metric space. An
incoplete metric space, S, has a Cauchy sequence (PL) which does
not converge (PL). The space is completed by adjoining the limits to the Cauchy
sequences. (The completion is always compoete (PL).) Thus, the completion of the
rationals is the real number system. But the completion depends on the metric. Thus,
for any prime, p, the rationals have a metric given by the
p-adic norm, so that the completion of the rationals then becomes
the set of p-adic numbers. Specifically, the completion
of a metric space, S, is the set of Cauchy sequences, and
S is isometrically contained in thi set as the constant sequences
.
complex conjugate. Given the complex
number, a + bi, for i = (-1)1/2,
its conjugate is a - bi.
complex fraction. A fraction (PL)
whose numerator, denominator (PL) are fractions.
complexification. Replacing a real
parameter or functand by one that is a complex number.
complex number. A number equivalent to
the form, a + bi, for i = (-1)1/2.
complex plane. The plane (PL) of
complex numbers (PL) as in the Argand diagram (PL).
complex unit. The complex number
z = a + bi, for i = (-1)1/2 has the
polar (PL) form, z = r cos q + sin q. When r = 1, it designates a complex
unit.
complex variable (functand). A
functand (PL) assuming complex (PL) values.
composite number. Any number that is
product of two or more prime (PL) factors. Equivalently, an integer (PL) that is
neither prime nor zero nor +1 nor -1.
composition of functions. For two
functions (or mappings) f, g, with the range (output, codomain) of
f contained in the domain (input) of g, their
composition is a new function h(x) = g[f(x>)], for all x in the domain of f. The usual notation is h = g ° f, or sometimes h = f ° g (usually with
x(f)). Function composition generally is not commutative but is
associative
composition series. A normal series
of subgroups (PL) whose factors are all simple (PL).
compound number. The sum of two or more
quantities of differing units.
computation. Calculating, especially by
numerical methods.
computational geometry. Study of
efficient algorithms for solving geometric problems, such as convex hull
(PL) of a point set and Voronoi diagram (PL).
concave function. The function, f(x) is concave on an interval (PL) iff - f(x)
is convex (PL) on this interval.
concave polygon. A polygon (PL)
such there is a segment initiating and terminating in the polygon's interior which
crosses the polygon's boundary in its extension. (PL convex polygon.)
concentric circles. Coplanar circles
with differing radii but same center.
conchoid of Nicomedes. A curve with
equation (x - a)2(x2 + y2) = b2x
2.
conditional statement. An implication (PL).
cone. A pyramid with circular
cross-section (PL). (PL conic sections.)
conic sections. In his classic work, "On
Conics", Appolonius of Perga (c. 262-190? BC) showed that the ellipse, parabola, hyperbola
can be derived as sections of a cone, hence the label, "conic sections", for these curves.
configuration. Arrangement of
geometric structures, such as points, lines, surfaces, curves.
confluent hypergeometric function. PL
hypergeometric function.
confocal. Of structures having same
focus (PL) or focii.
confocal conics. Two or more conics
with the same focii or axes of symetry, such as a system
of hyperbolas or ellipses or parabolas.
confocal conics. Conics with foci
(PL) coincident. (PL elliptical coordinates.)
conformal mapping. Preserves angles
.
congruence. The coincidence of two
geometric configurations (PL) under one or more rigid transformation (PL). A
congruence relation (PL) between numbers.
congruence relation. The relation between
two or more numbers yielding the same remainder (PL) when divided by the same divisor
or modulus> (PL).
congruent. The result of congruence (PL).
congruent matrices. Pl transformation
for congruent transformation.
congruent numbers. Two or more numbers yielding the same remainder (PL) when divided by the same
divisor or modulus (PL). PL also congruence relation.
conic. Graph (PL) of 2nd-order (PL) polynomial equation (PL) in two functands (PL), representable as
intersection of plane with a bipartite cone (PL), that is, as a conic section (PL).
conical surface. pL conical sections
.
conjugate radicals. a pair of
irrational numbers of the form a(b)1/2 + c(d)1/2
and a(b)1/2 - c(d)1/2, where
a, b, c, d are rational (PL) but (b)1/2,
(d)1/2 are not both rational. Also labeled conjugate surds.
conjugation. Taking a complex
conjugate (PL) of a number, a matrix, etc.
conjunction. Binary operation on two or
more instances of logical statement (PL) (proposition, PL) yielding a compound
statement which is true iff all component statements are true.
connected graph. With a path (PL)
from any to any other point of the graph.
connected set. Cannot be partitioned into
two nonepty subsets s. t. neither can be has points in common with closure (PL) of the
other.
connected space. Any two of its points
can be connected by a curve wholly within it.
connected surface. Surface which is a
connected space (PL).
connection. Condition on a vector
bundles providing for "differentiation" of sections, homologous to exterior
derivative of a function.
connective, logical. The connectives
of standard statement logic (PL)
are- conjunction (and), often denoted as ampersand, &;
- disjunction (or);
- conditional (if __ then __), often denoted by an arrow (->);
- biconditional (iff), often denoted by double arrow (<-->);
- negation (not), often denoted by tilde (~).
consistent. If a mathematical theory
contains no statement S such that S and
~S (the negation of S) are theorems (i.e.,
the theory has no contradictions), it is said to be consistent.
consistent system. A system of equations
such that the solution set is nonempty.
constant. A term assumed fixed in its
context.
constraint function. Any of a finite
number of conditios on the solution to an optimization (PL) problem.
constructible. An algorithm (PL)
exists and is known for constructing. Said of any proof which avoids such
nonconstructive appeals as tertium non data (a.k.a. proof by contradiction) (PL)
or axiom of choice (PL).
contact transformation. PL
transformation.
content. A nonnegative, finite,
monotone, additive, and subadditive set function on the class of all compact subsets of a measure
space.
continued fraction. A canoncal form
(PL) for a real number, of the form: r= d0 + (n
1/d1 + (n2/d2 + (n3/d3) + ...))).
If fraction terminates, the number is rational, otherwise it is irrational.
A real number can have two different but equivalent decimal representations, but
only one continued fraction, hence "canonical".
continued fraction factorization algorithm.
A prime factorization algorithm (PL) using residues (PL) produced in the
continued fraction of (mN)½ for well chosen
m to yield a square number. The algorithm solves
x2  y2 (mod n) by searching
for an n s. t. m2 (mod n) has
the smallest lower bound. Estimated to require about exp(2logloglog n)
½ steps. This was the fastest known algorithm until discovery of the
quadraticsieve (PL), which eliminated the 2 in the above square
root.
continuous. All elements of a structure are
within a neighborhood of nearby points. A necessary but not sufficient condition for
differentiable. PL smooth.
continuous at a point. If
differentiable (PL) at the point. If two functions are continuous at a point, their
rational operations are defined.
continuous function. Mapping into
an open set (PL) is from an open set.
continuous group. Having contuous
group operations. (PL contiuous at a point.)
continuum. The nondenumerable set
of real numbers. (PL denumerable numbers.)
contour integral. Obtained by
integration around a path ("cpuntour") in the complex plane, encircling a point onvr
in clockwise direction.
contraction (of a tensor). Setting
dissimilar indices equal and summing by the Einstein summation (PL) convention, thereby
reducing the rank of a tensor (PL).
contradual. PL quaternality.
contrapositive. Given a statement
(PL) of the form "if precedent statment is true, then the consequent statement is true", its
contrapositive is "if consequent statment is not true, then the precedent statement
is not true". The contrapositive has the same truth value as the original.
contravariant functor. A functor
which reverses the arrow. (PL covariant functor.)
contravariant tensor. The result of
multiplying a covariant tensor (PL) by a metric tensor (PL).
contravariant vector. An ordinary
vector is a contravariant tensor of rank 1.
converge. An iteration (PL) or
infinite sequence (PL) iff a value can be assigned to it.
converge absolutely. A series
(PL), Snsn converges
absolutely iff Sn|sn|
converges. If so, the sum is invariant under changes in ordering of addends.
convergent sequence. Sequence with
limit (PL).
convergent series. Series with limit
.
converse. Given a statement
(PL) of the form "if precedent statment is true, then the consequent statement is true", its
converse is "if conseqent statment is true, then the precedent statement is true". The
converse does not necessarily have the same truth value as the original. PL asserbility.
convex function. A function (PL),
f(x), on interval (PL), [a, b], iff, for
any two points, x1, x2 e
[a, b], we find f[½(x1 + x2]
y2 (mod n) by searching
for an n s. t. m2 (mod n) has
the smallest lower bound. Estimated to require about exp(2logloglog n)
½ steps. This was the fastest known algorithm until discovery of the
quadraticsieve (PL), which eliminated the 2 in the above square
root.
continuous. All elements of a structure are
within a neighborhood of nearby points. A necessary but not sufficient condition for
differentiable. PL smooth.
continuous at a point. If
differentiable (PL) at the point. If two functions are continuous at a point, their
rational operations are defined.
continuous function. Mapping into
an open set (PL) is from an open set.
continuous group. Having contuous
group operations. (PL contiuous at a point.)
continuum. The nondenumerable set
of real numbers. (PL denumerable numbers.)
contour integral. Obtained by
integration around a path ("cpuntour") in the complex plane, encircling a point onvr
in clockwise direction.
contraction (of a tensor). Setting
dissimilar indices equal and summing by the Einstein summation (PL) convention, thereby
reducing the rank of a tensor (PL).
contradual. PL quaternality.
contrapositive. Given a statement
(PL) of the form "if precedent statment is true, then the consequent statement is true", its
contrapositive is "if consequent statment is not true, then the precedent statement
is not true". The contrapositive has the same truth value as the original.
contravariant functor. A functor
which reverses the arrow. (PL covariant functor.)
contravariant tensor. The result of
multiplying a covariant tensor (PL) by a metric tensor (PL).
contravariant vector. An ordinary
vector is a contravariant tensor of rank 1.
converge. An iteration (PL) or
infinite sequence (PL) iff a value can be assigned to it.
converge absolutely. A series
(PL), Snsn converges
absolutely iff Sn|sn|
converges. If so, the sum is invariant under changes in ordering of addends.
convergent sequence. Sequence with
limit (PL).
convergent series. Series with limit
.
converse. Given a statement
(PL) of the form "if precedent statment is true, then the consequent statement is true", its
converse is "if conseqent statment is true, then the precedent statement is true". The
converse does not necessarily have the same truth value as the original. PL asserbility.
convex function. A function (PL),
f(x), on interval (PL), [a, b], iff, for
any two points, x1, x2 e
[a, b], we find f[½(x1 + x2]  ½ f[(x1 + x2].
convex hull (of point set). The
intersection (PL) of all sets containing a given point set. A problem in computational
geometry.
convex set. The segment (PL)
joining any pair of points does not depart from the set. (PL concave.)
convolution theorem. Given Fourier
functions, f, g, and Fourier transform,
F, then F[fg] = F[f] * F
[g].
coordinate. Any of an
n-tuple set of numbers which represents a point in
n-space.
coordinate axes. The n
-set of independent lines that uniquely specify any point in n-
space by its projections (PL) upon these lines.
coordinate basis. Set of independent
coordinates (PL) for a given dimension (PL) of space.
coordinate system. A system of number
n-tuples which represents a point in
n-space.
coordinate transformation. Any
formula (PL) expressing values (on an open set, PL) of one coordinate ystem
(PL) in terms of another coordinate system. Such a transformation is useful if
simplifies the manipulation. The transformation of Cartesian coordinates is
representative. The translation of axes is simple: x' = x + h, y' =
y + k, z' = z + l. The rotation of axes is critical and invokes the
concept of metric (PL): x = x' cos q - y' sin
q, y = x' sin q + y' cos q
. The validity of this is demonstrated by its matrix formation from
which one can derive its determinant:
½ f[(x1 + x2].
convex hull (of point set). The
intersection (PL) of all sets containing a given point set. A problem in computational
geometry.
convex set. The segment (PL)
joining any pair of points does not depart from the set. (PL concave.)
convolution theorem. Given Fourier
functions, f, g, and Fourier transform,
F, then F[fg] = F[f] * F
[g].
coordinate. Any of an
n-tuple set of numbers which represents a point in
n-space.
coordinate axes. The n
-set of independent lines that uniquely specify any point in n-
space by its projections (PL) upon these lines.
coordinate basis. Set of independent
coordinates (PL) for a given dimension (PL) of space.
coordinate system. A system of number
n-tuples which represents a point in
n-space.
coordinate transformation. Any
formula (PL) expressing values (on an open set, PL) of one coordinate ystem
(PL) in terms of another coordinate system. Such a transformation is useful if
simplifies the manipulation. The transformation of Cartesian coordinates is
representative. The translation of axes is simple: x' = x + h, y' =
y + k, z' = z + l. The rotation of axes is critical and invokes the
concept of metric (PL): x = x' cos q - y' sin
q, y = x' sin q + y' cos q
. The validity of this is demonstrated by its matrix formation from
which one can derive its determinant:
æ cos q sin q ö
ç ÷
è - sin q cos q ø
whose determinant equals cos2q +
sin2q = 1, a well-known trigonometric identity
.
corrigibility. PL incorrigibility
.
cosecant. For a right triangle
(PL), the ratio of the hypotenuse (PL) to the side opposite a given angle: the reciprocal
of the sine (PL) of a given angle or arc.
cosh (hyperbolic cosine). Relates to the
hyperbola (pl) as the circular (trigonometric) functions relate to the circle
: cosh x = ½(ex + e-x).
cosine. For a right triangle
(PL), the side adjacent (PL) to the right angle in ratio to the hypotenuse (PL) of
the triangle.
cotangent. The reciprocal of the
tangent (PL).
cotangent bundle (of manifold). Similar
to tangent bundle (PL) except that it is the set, (x, f), for
point, x, in manifold (PL), M, and f is a dual vector (PL) in the tangent space,
TM, to x e M. Denoted
TxM.
cotangent space. PL contangent bundle
.
coth (hyperbolic cotangent). Relates to
the hyperbola (pl) as the circular (trigonometric) functions relate to the
circle: coth x = (ex + e-x)/(ex -
e-x = (e2x + 1)/(e2x - 1).
countable. One-one correspondence to set
of all integers (PL). (For example, the set of rational numbers -- with proper
fractions "squezed" in between integral fractions -- can, nevertheless, be made one-one
correspondent with the integers, hence, are countable. But the real numbers cannot
be similarly assigned, so are not countable.)
covariant tensor. Denoted by lowered
indices (whereas contravariant tensor is denoted by raised indices). Any
tensor with transformation:  .
covariant vector. A covariant tensor
(PL) of rank 1; known in differential forms (PL) as a one-form, the
dual (PL) of a vector; known in Dirac notation as a bra (PL), the
dual of a ket (PL).
covering space. Given X, X' as locally arc-connected topological spaces (PL), then
(X, p) is a covering space iff p:X -> X' maps an
open subspace into an open subspace.
cover of a set (covering). Union
of sets containing the specified set. In the poset of subsets of a set, T, the poset element, S, uniquely covers T iff S
.
covariant vector. A covariant tensor
(PL) of rank 1; known in differential forms (PL) as a one-form, the
dual (PL) of a vector; known in Dirac notation as a bra (PL), the
dual of a ket (PL).
covering space. Given X, X' as locally arc-connected topological spaces (PL), then
(X, p) is a covering space iff p:X -> X' maps an
open subspace into an open subspace.
cover of a set (covering). Union
of sets containing the specified set. In the poset of subsets of a set, T, the poset element, S, uniquely covers T iff S  T = S and S
T = S and S  T = T (set-theoretically, S
T = T (set-theoretically, S 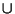 T = S and S
T = S and S  T = T).
coversine. 1 =
sin q: difference between radius (1)
and sine of angle (sin q constructed in a
unit circle.
Coxeter graph. A non-Hamiltonian
(PL) symmetric (PL) and cubic graph (PL) with 28 vertices (PL) and 42 edges
(PL).
Cramer's rule. An algorithm (PL)
for solving a system Ax = b of n independent
(nonzero det A, PL) linear equations (PL) in n
independent unknowns, where A denotes the matrix (PL) of coefficients
(PL); where x is the column vector whose entries are the n independent functands (PL); and b is the
column vector whose entries are the constant terms of the n linear
equations. The value for the jth functand equals the ratio whose
denominator (PL) is det A and whose numerator is the
determinant (PL) of the matrix obtained from A by replacing the
jth column with the entries of b.
critical function. The function at which
a given functional (PL) becomes extremized; homologous to a critical point (PL) in
ordinary calculus. A critical function satisfies the Euler-Lagrange equation, just as a
critical point satisfies f'(x) = 0. Also, labeled extremal.
critical point. The point at which f'(x) = 0 or does not exist. PL critical function.
critical value. A value in the range
(codomain, PL) of a function corresponding to the critical point (PL) in the domain
(PL) of the function.
cross-cap.The self-intersection of a
one-sided (nonorientable) surface, produced by puncturing once a surface (twice for cross
-handle), attaching two zips around the puncture (circling in same direction -- oppositely for
handle), lining up the zips for selfinterection, then zipping up. Essentially, a circular
hole which, when entered, exits from its opposite point -- although, topologically, these are
equivalent. The cross-cap has a segment of double points terminating as two "pinchpoints"
("Whitney singularities"). A cross-handle (PL) is homeomorphic (PL) to two cross-cps.
In traditional literature, a sphere with one cross-cap is a real projective plane (PL). A
cross-cap is one of three possible surfaces produced by sewing a Möboid (M. strip, M.
band) to the edge of a disk. (The others, a Boy surface and a Roman surface.)
Generated in manner of an orientable surface by a polynomial function: f(x, y, z) = (xz, yz, ½(z2 - z2), or in cylindrical
coordinates: x(u, v) = ½cos u sin (2v), y(u, v) = ½sin u sin
(2v), z(u, v0 = ½(cos2 v - cos2 u sin2 v), u e [0, 2p), v e [0, p/2]. (The equations can be multiplied by two to clear scaling
constant.)
cross-handle. A structure in topology
(PL) produced by twice puncturing a surface, attaching a zip (PL) around each puncture (circling
in the same direction -- unlike a handle, wherein circling is oppositely), pulling together zip
edges after one tube first passes through itself to match up zip directions, then zipping up.
In 3-D, the cross-handle contains a line of self-intersection. A cross-handles is
homeomorphic (PL) to two cross-caps. Dyck's theorem (PL) states that handles (PL)
and cross-handles are equivalent in the presence of cross-cap.
cross multiplication. For nonzero, b, d, a/b = c/d ->ad = bc,
crossmultiplying numerator of one fraction with denomilnator of other for an equivalent
result.
cross product. An anticommutative
operation on the vectors of Euclidean 3-space, denoted by a × b = c, where each of a, b, c is a vector. The
cross product is given by a× b = ||a||
||b|| u sin q, where ||-||
denotes the norm (magnitude) (PL) of a vector, and q denotes the
angle between vectors a,b and u is a
unit vector perpendicular to the plane of A, B such that
a, b, c form a right-handed system. The cross product
distributes over vector addition, commutes with scalar multiplication
and is zero iff a, b are parallel or at least one is the
null vector (PL). ||a × b|| is the
area of the parallelogram with sides a, b. Also, labeled
vector product. (PL cross product, alternative to).
cross product, alternative to. The
vector operation (PL) is formulated quasi-axiomatically in the literature. But it
arises generatively in considering a system of two inner products of vector. At one
stage of the explication, a choice must be made concerning an entity in the development. One
choice leads to vector cross product, the other to multivector outerproduct (PL).
cross ratio (anharmonic ratio). A
defining property of projective geometry, the cross ratio is invariant under any
projection (PL). Given four distinct collinear (PL) lines, the cross ratio,
(AB, CD), is the quotient of the ratio in which C divides AB by the ratio in which D divides AB. If the abscissas (or
ordinates) of four points are x1, x2, x3,
x4, the cross ratio is [(x3 - x1
)(x4 - x2)] / [(x3 - x2)(x4 - x
1)]. If no ordering of the four points yields a harmonic ratio (PL), then
(relative to ordering of points) six distinct values of the c. r. exist. Given four distinct
concurrent lines, L1, L2, L3, L4
, with (respective) slopes, m1, m2,
m3, m4, the cross ratio of the four lines is [(m3 - m1)(m4 - m2)] / [(m3 - m
2)(m4 - m1)].
cross section (of solid). Plane figure
created by intersecting the solid by a plane (PL).
Crout's algorithm. Pl root-finding
algorithm.
cruciform curve. Curve of equation,
x2y2 - a2x2 - b2y2
= 0. (Also called cross curve and policeman on point duty curve.)
cube. A six-sided polyhedron (PL)
(a hexahedron) with congruent square faces (with right angle face angles); a cuboid
(PL) with equal edges. The cube is one of five Pythagorean-Platonic solids (PL).
cube of a number. The cube of a
number n is n · n · n = n3
. (The use of such "geometric" language for a numbers derives from the Pythagorean
geometric number theory in which numbers were constructed as configurations of pebbles or
whatever.)
cubic. Of, or relating to, a geometric
cube (PL) or the cube of a number or quantity (PL).
cubical parabola. The planar Cartesian
coordinate graph of equation y = x3.
cubic curve. A plane curve of the
equation f(x,y) = 0 where f(x,y) is a cubic
polynomial (PL) in x, y.
cubic (trivalent) graph. All with
degree three nodes (PL 3-degree graphs). Such graphs only for an n
even number of nodes.)
cubic polynomial. A polynomial
(PL) with at least one term of degree three and no term of higher degree.
cubic spline. A spline constructed
of piecewise (PL) third-order polynomials passing through m
control points (PL).
cuboctahedron (dymaxion, heptaparallelohedron)
. This Archimedean *simiregular) solid (PL), with sections common to cube
(PL) and octahedron, is listed in the literature as A1, although Heron
of Alexandria (c. 75AD) said Archimedes (287?-212BC) ascribed it to Plato (427-327?BC). It is one
of the two convex quasiregular polyhedra (PL). Its dual polyhedron (PL) is the
rhombic polyhedron in which it can be inscribed. The mineral argentite (Ag2S)
forms cuboctahedral crystals. (Buckminster Fuller (1895-1983) called it the dymaxion.)
cuboid (rectangular parallelopiped).
Composed of thre pairs of rectangular faces opposite to each other, joined by right angles to
each other.
cup operator. Denotes union of
sets: _
T = T).
coversine. 1 =
sin q: difference between radius (1)
and sine of angle (sin q constructed in a
unit circle.
Coxeter graph. A non-Hamiltonian
(PL) symmetric (PL) and cubic graph (PL) with 28 vertices (PL) and 42 edges
(PL).
Cramer's rule. An algorithm (PL)
for solving a system Ax = b of n independent
(nonzero det A, PL) linear equations (PL) in n
independent unknowns, where A denotes the matrix (PL) of coefficients
(PL); where x is the column vector whose entries are the n independent functands (PL); and b is the
column vector whose entries are the constant terms of the n linear
equations. The value for the jth functand equals the ratio whose
denominator (PL) is det A and whose numerator is the
determinant (PL) of the matrix obtained from A by replacing the
jth column with the entries of b.
critical function. The function at which
a given functional (PL) becomes extremized; homologous to a critical point (PL) in
ordinary calculus. A critical function satisfies the Euler-Lagrange equation, just as a
critical point satisfies f'(x) = 0. Also, labeled extremal.
critical point. The point at which f'(x) = 0 or does not exist. PL critical function.
critical value. A value in the range
(codomain, PL) of a function corresponding to the critical point (PL) in the domain
(PL) of the function.
cross-cap.The self-intersection of a
one-sided (nonorientable) surface, produced by puncturing once a surface (twice for cross
-handle), attaching two zips around the puncture (circling in same direction -- oppositely for
handle), lining up the zips for selfinterection, then zipping up. Essentially, a circular
hole which, when entered, exits from its opposite point -- although, topologically, these are
equivalent. The cross-cap has a segment of double points terminating as two "pinchpoints"
("Whitney singularities"). A cross-handle (PL) is homeomorphic (PL) to two cross-cps.
In traditional literature, a sphere with one cross-cap is a real projective plane (PL). A
cross-cap is one of three possible surfaces produced by sewing a Möboid (M. strip, M.
band) to the edge of a disk. (The others, a Boy surface and a Roman surface.)
Generated in manner of an orientable surface by a polynomial function: f(x, y, z) = (xz, yz, ½(z2 - z2), or in cylindrical
coordinates: x(u, v) = ½cos u sin (2v), y(u, v) = ½sin u sin
(2v), z(u, v0 = ½(cos2 v - cos2 u sin2 v), u e [0, 2p), v e [0, p/2]. (The equations can be multiplied by two to clear scaling
constant.)
cross-handle. A structure in topology
(PL) produced by twice puncturing a surface, attaching a zip (PL) around each puncture (circling
in the same direction -- unlike a handle, wherein circling is oppositely), pulling together zip
edges after one tube first passes through itself to match up zip directions, then zipping up.
In 3-D, the cross-handle contains a line of self-intersection. A cross-handles is
homeomorphic (PL) to two cross-caps. Dyck's theorem (PL) states that handles (PL)
and cross-handles are equivalent in the presence of cross-cap.
cross multiplication. For nonzero, b, d, a/b = c/d ->ad = bc,
crossmultiplying numerator of one fraction with denomilnator of other for an equivalent
result.
cross product. An anticommutative
operation on the vectors of Euclidean 3-space, denoted by a × b = c, where each of a, b, c is a vector. The
cross product is given by a× b = ||a||
||b|| u sin q, where ||-||
denotes the norm (magnitude) (PL) of a vector, and q denotes the
angle between vectors a,b and u is a
unit vector perpendicular to the plane of A, B such that
a, b, c form a right-handed system. The cross product
distributes over vector addition, commutes with scalar multiplication
and is zero iff a, b are parallel or at least one is the
null vector (PL). ||a × b|| is the
area of the parallelogram with sides a, b. Also, labeled
vector product. (PL cross product, alternative to).
cross product, alternative to. The
vector operation (PL) is formulated quasi-axiomatically in the literature. But it
arises generatively in considering a system of two inner products of vector. At one
stage of the explication, a choice must be made concerning an entity in the development. One
choice leads to vector cross product, the other to multivector outerproduct (PL).
cross ratio (anharmonic ratio). A
defining property of projective geometry, the cross ratio is invariant under any
projection (PL). Given four distinct collinear (PL) lines, the cross ratio,
(AB, CD), is the quotient of the ratio in which C divides AB by the ratio in which D divides AB. If the abscissas (or
ordinates) of four points are x1, x2, x3,
x4, the cross ratio is [(x3 - x1
)(x4 - x2)] / [(x3 - x2)(x4 - x
1)]. If no ordering of the four points yields a harmonic ratio (PL), then
(relative to ordering of points) six distinct values of the c. r. exist. Given four distinct
concurrent lines, L1, L2, L3, L4
, with (respective) slopes, m1, m2,
m3, m4, the cross ratio of the four lines is [(m3 - m1)(m4 - m2)] / [(m3 - m
2)(m4 - m1)].
cross section (of solid). Plane figure
created by intersecting the solid by a plane (PL).
Crout's algorithm. Pl root-finding
algorithm.
cruciform curve. Curve of equation,
x2y2 - a2x2 - b2y2
= 0. (Also called cross curve and policeman on point duty curve.)
cube. A six-sided polyhedron (PL)
(a hexahedron) with congruent square faces (with right angle face angles); a cuboid
(PL) with equal edges. The cube is one of five Pythagorean-Platonic solids (PL).
cube of a number. The cube of a
number n is n · n · n = n3
. (The use of such "geometric" language for a numbers derives from the Pythagorean
geometric number theory in which numbers were constructed as configurations of pebbles or
whatever.)
cubic. Of, or relating to, a geometric
cube (PL) or the cube of a number or quantity (PL).
cubical parabola. The planar Cartesian
coordinate graph of equation y = x3.
cubic curve. A plane curve of the
equation f(x,y) = 0 where f(x,y) is a cubic
polynomial (PL) in x, y.
cubic (trivalent) graph. All with
degree three nodes (PL 3-degree graphs). Such graphs only for an n
even number of nodes.)
cubic polynomial. A polynomial
(PL) with at least one term of degree three and no term of higher degree.
cubic spline. A spline constructed
of piecewise (PL) third-order polynomials passing through m
control points (PL).
cuboctahedron (dymaxion, heptaparallelohedron)
. This Archimedean *simiregular) solid (PL), with sections common to cube
(PL) and octahedron, is listed in the literature as A1, although Heron
of Alexandria (c. 75AD) said Archimedes (287?-212BC) ascribed it to Plato (427-327?BC). It is one
of the two convex quasiregular polyhedra (PL). Its dual polyhedron (PL) is the
rhombic polyhedron in which it can be inscribed. The mineral argentite (Ag2S)
forms cuboctahedral crystals. (Buckminster Fuller (1895-1983) called it the dymaxion.)
cuboid (rectangular parallelopiped).
Composed of thre pairs of rectangular faces opposite to each other, joined by right angles to
each other.
cup operator. Denotes union of
sets: _  _.
cup product. A product on
cohomology classes (PL), denoted by the wedge symbol: _
_.
cup product. A product on
cohomology classes (PL), denoted by the wedge symbol: _  _.
curl. For vector field, F, this is: curl(F)
_.
curl. For vector field, F, this is: curl(F) 
 X F, normal to the plane of maximum "circulation". The
tensor field is: (
X F, normal to the plane of maximum "circulation". The
tensor field is: ( X T)amn
= eamn Tn;m,, where "," denotes covariant
derivative (PL).
curtate (contracted) cycloid. Given a
rolling circle, of radius r, this curve is the traced by a point
inside the circle of radius, s < r. Parametric equations: x = af - b sin f, y = a - b cos
f.
curvature. The curvature
of a circle of radius r at
any point on the circle is defined as 1/r. In general, the
curvature of a curve is measured by the rate of change of the unit normal(s)
to the curve with respect to arc length s measured along
the curve. If a is the angle of normal (or tangent) to a
plane curve, the curvature at a point of the curve is equal to
a/ds. This curvature is equal to the curvature of
the circle that most closely approximates the curve at the point.
curve. Geometrically, any
continuous image of a closed interval. Algebraically, in n-space,
a set of n parametric equations
xi = ai(t), which (in integration theory) is equivalent
to a 1-cube.
curve tracing. Drawing a curve's
graph (PL), using analytic tools (symmetry, asymptotes, and derivatives to
determine slope, critical points, convexity, etc.), and calculating points on the graph.
cusp. A double point on a curve
where the tangent vector undergoes a change of sign as the curve unfolds.
cusp catastrophe. PL catastrophe.
cuspidal cubic (semicubical parabola).
The evolue of a parabola.
cut. Given a weighted and
undirected graph, along with a grphical partition of graph's vertices. A cut
can be defined w. r. to the two vertex sets s. t. the weight of the cut is sum of the weights
crossing the cut.
cycle of a permutation). A subset
of a permutation (PL) whose members interchange positions. Given permutation
{1, 2, 3, 4}, then {1, 3. 4} is a 3-cycle
(1 -> 3 -> 4 -> 1); {2} is a 1-cycle (
2 -> 2); etc.
cyclic group. A group of finite
powers of a fixed element (generator) such that the highest power equals the
identity element (PL) of the group. All finite groups of prime order (PL) are cyclic.
All cyclic groups are Abelian (PL) and are unique for every order,
n
X T)amn
= eamn Tn;m,, where "," denotes covariant
derivative (PL).
curtate (contracted) cycloid. Given a
rolling circle, of radius r, this curve is the traced by a point
inside the circle of radius, s < r. Parametric equations: x = af - b sin f, y = a - b cos
f.
curvature. The curvature
of a circle of radius r at
any point on the circle is defined as 1/r. In general, the
curvature of a curve is measured by the rate of change of the unit normal(s)
to the curve with respect to arc length s measured along
the curve. If a is the angle of normal (or tangent) to a
plane curve, the curvature at a point of the curve is equal to
a/ds. This curvature is equal to the curvature of
the circle that most closely approximates the curve at the point.
curve. Geometrically, any
continuous image of a closed interval. Algebraically, in n-space,
a set of n parametric equations
xi = ai(t), which (in integration theory) is equivalent
to a 1-cube.
curve tracing. Drawing a curve's
graph (PL), using analytic tools (symmetry, asymptotes, and derivatives to
determine slope, critical points, convexity, etc.), and calculating points on the graph.
cusp. A double point on a curve
where the tangent vector undergoes a change of sign as the curve unfolds.
cusp catastrophe. PL catastrophe.
cuspidal cubic (semicubical parabola).
The evolue of a parabola.
cut. Given a weighted and
undirected graph, along with a grphical partition of graph's vertices. A cut
can be defined w. r. to the two vertex sets s. t. the weight of the cut is sum of the weights
crossing the cut.
cycle of a permutation). A subset
of a permutation (PL) whose members interchange positions. Given permutation
{1, 2, 3, 4}, then {1, 3. 4} is a 3-cycle
(1 -> 3 -> 4 -> 1); {2} is a 1-cycle (
2 -> 2); etc.
cyclic group. A group of finite
powers of a fixed element (generator) such that the highest power equals the
identity element (PL) of the group. All finite groups of prime order (PL) are cyclic.
All cyclic groups are Abelian (PL) and are unique for every order,
n  1, so that cyclic groups of the same order are
isomorphic.
cycloid. Given a rolling circle,
the cycloid is the path traced out by a point on the perimeter of the circle. (PL
brachistochrone and tautachrone.
cycloidal. PL cycloid.
cyclotomic polynomial. Any
polynomial (PL) of the form g(x) = xp-1
+ xp-2 + ... + x + 1 = (xp - 1)/(x - 1),
for prime p. Such a polynomial is irreducible over the real
numbers.
cyclotomy. Geometrically,
division of a circle into equal sectors, or consructing regular polygons. Analytically,
extracting nth roots of unity.
cylinder. The lateral surface
(PL) of a solid with circular cross-section s. t. centers of circles lie along
a line segment. Topologically: the Cartesian product (PL) of a circle and a
segment.
cylinder function. Any solution
of Bessel's equation (PL).
cylindrical coordinates. Generalization
to 3-D of 2-D polar coordinates (PL). Parametric equations: r =
1, so that cyclic groups of the same order are
isomorphic.
cycloid. Given a rolling circle,
the cycloid is the path traced out by a point on the perimeter of the circle. (PL
brachistochrone and tautachrone.
cycloidal. PL cycloid.
cyclotomic polynomial. Any
polynomial (PL) of the form g(x) = xp-1
+ xp-2 + ... + x + 1 = (xp - 1)/(x - 1),
for prime p. Such a polynomial is irreducible over the real
numbers.
cyclotomy. Geometrically,
division of a circle into equal sectors, or consructing regular polygons. Analytically,
extracting nth roots of unity.
cylinder. The lateral surface
(PL) of a solid with circular cross-section s. t. centers of circles lie along
a line segment. Topologically: the Cartesian product (PL) of a circle and a
segment.
cylinder function. Any solution
of Bessel's equation (PL).
cylindrical coordinates. Generalization
to 3-D of 2-D polar coordinates (PL). Parametric equations: r =  (x2 + y2); q = arctan(y/x); z = z
.
(x2 + y2); q = arctan(y/x); z = z
.
 0. Formally,
dcapacity
0. Formally,
dcapacity  - lime
- lime 0+(ln N)/(ln e) (if the limit exists), for N the number of elements forming a finite cover (PL) of the appropriate metric
space, with e a bound on the diameter of the involved sets.
If elements of a fractal are equally visited, dcapacity = d
information, where the latter is the information dimension. Result:
dcorrelation
0+(ln N)/(ln e) (if the limit exists), for N the number of elements forming a finite cover (PL) of the appropriate metric
space, with e a bound on the diameter of the involved sets.
If elements of a fractal are equally visited, dcapacity = d
information, where the latter is the information dimension. Result:
dcorrelation  dinformation
dinformation
 dcapacity, where the correlation dimension is
conjectured to be equal to the trapdoor dimension (PL) .
dcapacity, where the correlation dimension is
conjectured to be equal to the trapdoor dimension (PL) . .
. 2 mutually perpendicular lines intersecting at a single point,
called the origin.
2 mutually perpendicular lines intersecting at a single point,
called the origin. gf(z) = S
ak Res(f(z)) = (2ip(a-1 + b-1 +
c-1 + d-1 + ... + n-1).
gf(z) = S
ak Res(f(z)) = (2ip(a-1 + b-1 +
c-1 + d-1 + ... + n-1).
 , 1
, 1 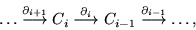 , provided that
, provided that 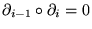 . The spaces, Ci, are
modules, Abelian groups, etc. Chain complexes define or compute homology groups
; cochain complexes for cohomology. The chain concept is critical in the
definition of a solvable group (PL).
. The spaces, Ci, are
modules, Abelian groups, etc. Chain complexes define or compute homology groups
; cochain complexes for cohomology. The chain concept is critical in the
definition of a solvable group (PL). .
. B) = n(A) + n(B) - n(A
B) = n(A) + n(B) - n(A  B). PL
sieving as clusion.
B). PL
sieving as clusion. .
. T = S and S
T = S and S  T = T (set-theoretically, S
T = T (set-theoretically, S  T = S and S
T = S and S  X T)amn
= eamn Tn;m,, where "," denotes covariant
derivative (PL).
X T)amn
= eamn Tn;m,, where "," denotes covariant
derivative (PL). (x2 + y2); q = arctan(y/x); z = z
.
(x2 + y2); q = arctan(y/x); z = z
.