- d'Alembertian
. - A vector (PL)
amd
tensor operator. Writing a partial derivative with respect to x
as ƒx, the d'Alembertian often appears in
the literature as: ¤2

 2 - 1/c2ƒt2, where
c is the vacuum speed of light. In tensor notation, ¤2 f
2 - 1/c2ƒt2, where
c is the vacuum speed of light. In tensor notation, ¤2 f  (glk f;l
);l = glk ƒ
xlxkf - G ƒxl
f. (The
d'Alembertlian can more directly, and more generally, be defined in multivector theory
[31] (by variation on the multiproduct. PL) as
(glk f;l
);l = glk ƒ
xlxkf - G ƒxl
f. (The
d'Alembertlian can more directly, and more generally, be defined in multivector theory
[31] (by variation on the multiproduct. PL) as  2 - 1/u2 ƒt2, where u
has the dimension of velocity.)
2 - 1/u2 ƒt2, where u
has the dimension of velocity.)
- d'Alembert's Principle from Newton's Law (Lanczos)
. -
On p. 88 of his book, The Variational Principles of Mechanics, first published in
1949, Cornelius says: "With a stroke of genius the eminent French nathematician and philosopher
d'Alembert (1717-1783) succeeded in extending the applicability of the principle of virtual
work from statics to dynamics. The simple but far-reaching idea of d'Alembert can be approached
as follows. We start with the fundamental law of motion: 'mass times acceleration equal moving
force' [vectors underlined]:
mA = F (1)
and rewrite this equation in the form
F _ mA = 0. (2)
We now define a vector I by the equation
I = -mA. (3)
This vector I can be considered as a force,
created by the motion. We call it the 'force of inertia'. With this concept
the equation of Newton can be formulated as follows:
F + I = 0. (4)
Apparently nothing is gained, since the intermediate step (3) gives merely
a new name to the negative product of mass times acceleration. It is exactly
this triviality which makes d'Alembert's principle such an ingenious invention
and at the same time so open to distortion and misunderstanding." This Pricinciple, reducing
dynamics to statics is actually antitonic, as showm elsewhere.
- d'Alembert's Principle and Newton's Law from The Antitonic
Principle (Hays)
. - Consider the antitone: J * K = CONSTANT. (1)
Take the logarithm of (1): log J + log K = 0. (2)
Relabel: F = log J, I = log K ->
F + I = 0, d'Alembert's Principle. (3)
Relabel: I = -A. (4)
From (3), (4), F - mA = 0, or
F = mA (5), Newton's Law (implicitly antitonic). PL
Lagrange's Principle as Antitonic, Hamilton's Principle as Antitonic.
- Darboux's theorem
. - Provides formula
for expanding functions as infinite series, with a Taylor series (PL) as a
special case. Let f(x) be analytic at all points along a
line and let f(t) be any polynomial (PL)
of degree n in t. For 0
 t
t  1, differentiation (PL) yields:
DtS
1, differentiation (PL) yields:
DtS m-1 (-1)m(z - a)m f(n - m)(t)f
m(a + t(z - a)), which can be integrated (PL), (A Taylor series
evolves by setting f(t - 1)n and
letting n ->
m-1 (-1)m(z - a)m f(n - m)(t)f
m(a + t(z - a)), which can be integrated (PL), (A Taylor series
evolves by setting f(t - 1)n and
letting n ->  .)
.)
- decagon
. - A
constructible regular (PL) 10-sided polygon (PL).
- decidable
. - A theory is
decidable iff an algorithm (PL) exists for determining if a given sentence
(PL) is an element of the theory.
.
- decimal
. - A word derived from Latin
meaning "ten".
- decimal numeration system
. - A positional
(PL) numeration system Based upon ten elements, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
. Thus, the symbol, 27458, denotes 2 X 10
3 + 7 X 103 + 4 X 102 + 5 X 10 + 8. The position of a
digit (from right-most position) denotes its power of ten (starting in zero power on
right). This system is believed to derive from the normal ten fingers of human hands, hence
the use of the word, "digit", for both finger and numeral.
- Dedekind cut
. - A partitioning
("cut") of the rational numbers into nonempty sets, S1
, S2, s. t. all numbers of S1 are
less than the numbers of S2 and S
1 has no greatest number -- allowing for an irrational number in
any "cut".
- Dedekind ring
. - A commutative ring
(PL) which is a Noetherian ring (PL) and integral domain (PL) containing the set of
algebraic integers (PL) in its field of rationals (PL) s.t. its prime ideal
(PL) is also a maximal ideal.
- deficiency (binomial)
. - Given binomial
coefficient, C(n, k), let n - k + 1 = ai
bi, with 0
 i
i  k, and with bi containing only those
prime factors greater than k. Then the number
i for which bi > 1 is the deficiency of
C(n, k).
k, and with bi containing only those
prime factors greater than k. Then the number
i for which bi > 1 is the deficiency of
C(n, k).
- del operator
. - PL nabla operator.
- delta operator
. - A shift-invariant
operator (PL), Q s. t. Qx is a nonzero
constant: Qa = 0, for each constant a; for
degree n-polynomial p(x), Qp(x) is of degree
n - 1; each delta sequence has a unique basic polynomial sequence
(PL).
- De Morgan's duality law
. - For every
statement (a.k.a. proposition) (PL) involving logical operators "and", "or", there
is a corresponding logical statement interchanging these operators.
- Denjoy integral
. - Extension of the
TRiemann integral (PL) and the Lebesque integral (PL).
- denominator
. - Given a rational number
("fraction") -- PL -- of the number n/d, the number d is the denominator of this mathematical structure, whereas n is its numerator (PL). (Also PL least common
denominator.)
- dense
. - A set S
is dense in set T if T = S
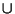 R where R is the limit of sequences of elements in S. Thus, the set of rational numbers is dense in the set of real
numbers.
R where R is the limit of sequences of elements in S. Thus, the set of rational numbers is dense in the set of real
numbers.
- dependent variable
. - The functand
(PL) in a function which is determined by another (independent) functand of the
function.
- de Rham cohomology
. - A formal arrangement
for analytic problems, the kth deRham cohomology vector space
is the space of all differential k-forms with exterior
derivative (PL) equal to zero, modulo all boundaries of (k - 1)
-forms. If so, this is the setup of the problem, it is the ordinary vector space.
- derangement
. - A permutation (PL)
s. t. no element retains its original position.
- derivation
. - From "derive", a sequence of
logical or computational steps from one structure to another. (PL derivation algebra.)
- derivation algebra
. - Given an algebra
(PL), A, over a field (PL), a derivation is a
linear operator (PL), D, s. t. D(xy) = (Dx)y +
x(Dy), for all x, y e A. The set D(A) of all derivatives of A in the
subspace (PL) of an associative algebra (PL) of all the linear operators
(PL) on A is a Lie algebra (PL), labeled a derivation
algebra.
- derivative
. - PL derivative operator
/
- derivative operator
- For the
standard notation, a prototype is d/dx, resembling a "fraction". This
misleading notation gives rise to Menger's "trivial" interpretation of calculus
due to its "atrocious languge", alluded to on the FRONTPAGE of this Website.
It actually is a profound theorem that (dy/dx)*(dx/dy)
= 1, although the notation resembles the "cancellation of fractions":
(2/3)*(3/2) = 1. The "nonfractional" Leibnitz
derivative notation avoids this confusion:
(Dxy)*(Dyx) = 1.
- Desargues' theorem
. - Given two triangles,
ABC, A'B'C', with three straight lines joining the vertices of opposite
sides. If these lines meet in a point (perspectival point,), then the three
intersectiions of pairs of correspomding sides lie on a straight line (perspectival axis
). That is, two triangles which are perpective from a point are also [erspective
from a line. This theorem is self-dual under the duality principle (PL) of
projective geometry (PL).
- Descartes' rule of signs
. - Determines
maximum number of positive and negative real roots of a polynomial
equation/ Proceeding from lower power to highest, the sign change number is the
number of positive real roots. Changing the power carrier to its negative yields a test
equation for counting the negative real roots. Thus, 5x7 + 3x6
- 2x5 + 8x3 - 2x2 + 9x - 4 = 0 has 5 sign
changes, hence, a maximum of 5 positive real roots. Then 5
(-x7) + 3(-x6) - 2(-x5) + 8(-x3) - 2(-x2) +
9(-x) - 4 = -5x7 + 3x6 + 2x5 - 8x3 + 2x2 -
9x - 4 = 0 has 4 sign changes, hence, the original equation has a maximum of
4 negative real roots. It can have, at most, 7 real roots, encompassed within this sum of
5 + 4 = 9.
- descending chain condition
. - The
dual of ascending chain condition (PL).
- determinant
. - A "square" array of
elements (numbers, etc.). usually written as:
æ e11 e12 ... e1nö
ç e21 e22 ... e2n÷
ç ............. ÷
è en1 en2 ... 3nnø
A determinant of numbers equals a single number, which is computed by the Laplacian
rule (PL). A matrix has an associated determinint iff it is square.
- devil's curve
. - Studied by G. Cramer
(1704-17520 in 1750, its equation is: y4 - a2y
2 = x4 - b2x2
.
- diagonal
. - In a polygon, the
diagonal connects nonintersecting vertices. In a diagonal matrix, the only
non-null elements are those with equal row and column indices.
- diagonalizable matrix
. - A square matrix
, M, is diagonalizablie iff it can be written as the
"conjugate" product, M = UDU-1, where D
is a diagonal matrix (PL) whose entries are the eigenvalues of M and the entries of U are the associated
eigenvectors.
- diagonal matrix
. - PL diagonal.
- diagram
. - PL standard dictionary entry.
- diameter
. - A chord (PL) passing
through and bisected by the center of a circle, conic, or solid of revolution generated by
a conic. For example, a diameter of a parabola (having its center at the point at infinity
on its axis) is a ray parallel to the axis of the parabola; it bisects chords parallel to the
line tangent to the parabola at the endpoint of the ray.
- Dido's problem
. - Find the geometric figure
bounded by a line which has the maximum perimater. Solution: semicircle. (Problem
appears in The Aeniad, written by the Roman poet, Vergil (70-19 BC)).
- diffeomorphism
. - A map betweeem
manifolds s. t. the map is differentiable (PL) with differentiable inverse
.
.
- difference
. - Result of a subtraction
operation.
- difference equation
. - PL finite
difference.
- difference operator
. - PL finite
difference.
- differentiable function
. - PL analytic
function.
- differentiable manifold
. - PL smooth
manifold.
- differential
. - PL differential form
.
- differential calculus
. - The arithmetic
of sets of functions of numbers (or the algebra) obtained by adjoining (to the
finitary operations of arithmetic) the transfinitary (PL) operation of
limit (PL).
- differential equation
. - An equation
containing one or more derivatives (PL) or differentials (PL).
- differential (k-)form
. - A completely
antisymmetric homogeneous r-tensor on a differentiable
n-manifold, where 0
 r
r  n. These form a Grassmannian algebra (subsystem of a
Clifford algebra, PL) labled the algebra of differential forms.
n. These form a Grassmannian algebra (subsystem of a
Clifford algebra, PL) labled the algebra of differential forms.
- differential geometry
. - Study of
metrical (PL) structures on Riemann manifolds. (PL differential topology.)
- differential topology
. - Study of
nometrical structures on Riemann manifolds. (PL differential geometry.)
- differentiation
. - Operational formation
of limits (PL) of difference functions (PL)
- digit
. - A numeral (PL) in a
number declaration.
- dihedral
. - PL standard dictionary.
- dihedral angle
. - The angle between two
planes.
- dihedral group
. - The group (PL)
of symmetries (PL) of an n-sided regular polygon; denoted
Dn.
- dilation
. - A similarity (PL)
transformation (PL) which transforms a line into a parallel line whose length
is a fixed multiple of the original line. A trivial dilation is a translation (PL). Any
other is a central dilation. Two triangles related by a central dilation are labeled
perspective triangles since the lines joining their vertices are concurrent. Thus,
a dilation is a translation concatenated with an expansion.
- dimension
. - One of the units (gnomons,
PL) associated with a physical quantity, physically expressable in terms of the fundamental
quantities of mass, length, time, and charge. It has been noted that the plane,
for example, is 2-D only because we choose to make the point the 0-D space-gnomon,
making the line segment 1-D and the plane 2-D, because it can be determined by
two independent numbers. However, we are free to make the circle the space-gnomon,
determined by three number (2 for center, 1 for radius), making the plane 3-D. (PL
activithm.) For other concerns about dimension,
- dimensional analysis
. - The
techniques for judging the correctness of equations by considering the units of measurement
of the variables in the equations:
- the units on the left side of the equation must be the same as on the right side;
- by changing measure functands, replace physical constants by dimensionless numbers (PL)
that remain invariant regardless of the units of measurement chosen
. (Note that Gerhard
A. Blass, in his book, Theoretical Physics, 1962, pp. 236-43, shows that Ludwig Boltzmann
(1844-1906) -- in deriving the most probable distribution of molecules according to Maxwell-Boltzmann
statistics -- just missed discovering the quantum constant of action, h, 20 years before Max Planck (1858-1938), by failing to write a constant of integration
and consider its dimensional form of ACTION).
- dimensional analysis algebra
. - The FORMS
of dimensional analysis (PL) can be used an an algebra for deriving other FORMS
from basic FORMS. Thus, the Planck-Einstein Law and the de Broglie Law of
QUANTICS -- mixing terms such as momentum, energy from MECHANICS with terms such as
frequency, wavelengthfrom OPTICS-ELECTROMAGNETICS -- can both be derived from the
photonic law: ln = c. The
intermediary is the concept of ACTION, h, from Lagrange's Principle,
applicable both in MECHANICS and OPTICS-ELECTROMAGNETICS. To derive deB, we start with the
Photonic Law (PL), which dimensionally is [ln]
= [c] = [L T-1]. Compare with dimensional FORM of ACTION: [h] = [M L2 T-1]. Now, a dimensional part of the latter is
[M L T-1], equivalent to that for momentum: [p] = [M LT-1]; and this becomes dimensionally equivalent to
ACTION by bring in length: [h] = [p L]. And we can obtain
a term of length via the wavelength of the photonic law:
[l] = [L]. Hence, we have h = pl , which is de Broglie's Law. To derive PE, we start with
the knowledge that light involves kinetic energy, which we wish to introduce into
some part of PL. Now, dimensionally [E] = [M L2
T-2]. Using Planck's CONSTANT as intermediary: [h] =
[(M L2)T-1]. Thus: [E] = [hT-1].
Taking WAVELENGTH from PL, we have: [El] =
[hLT-1]. On the right, we can use the PL VACCUM LIGHT SPEED,
c: [El] = [hc], for the ANTITONIC PE formula,
El = hc. Converting to the standard form of
PE, first take E = h(c/l), and the
parenthetical expression is Photonically c/l =
n, yielding the standard PE form, E =
hn. So, we find, by DIMENSIONAL ALGEBRA, that DB and PE are
IMPLICIT in PL, mixing MECHANICS with OPTICS and ELECTROMAGNETICS. (What else is possible by
DIMENSIONAL ALGEBRA?)
- dimensionless number
. - A number
with no associated unit of measure (PL) (such as square feet or pounds). In the
ratio of two numbers with the same unit of measure, the common unit "divides out".
- dimension theory
. - The branch of
topology that deals with various definitions of dimension. And PL measurement scales.
- Diophantine analysis
. - PL diophantine
equations.
- diophantine equations
. - A vast and often
difficult field of MATHEMATICS, named for Greek mathematician, Diophantus (c. 250 AD).
Let f(x1, x2, ..., xn) be a polynomial
in x1, x2, ..., xn with integer
coefficients. It is Diophantine if solutions must be integral. Linear Example:
4x1 + 6x2= 24. A solution is
x1 = 3, x2 = 2. (For a linear equation,
a1x1 + a2x2 + ... +
anxn = b, to be INTEGRALLY SOLVABLE, b
must BE DIVISIBLE BY gcd(a1, a2, ...,
an) -- as you find in the above example, wherein
gcd(4, 6) = 2 divides 12. (Linear Diophantine equations have been useful in modeling
chemical crystals.) Conditions have been found for SOLVABILITY of higher degree Diophantine
equations. In 1912, the great German mathematician, David Hilbert (1862-1943), gave a List
of Problems to be Solved -- one of which was a general solution for Diophantine equations.
Eventually, it was proven that no such general solution can exist.
- diophantus problem
. - The Greek mathematician,
Diophantus (200?-284? A.D.), has been called "The Father of Algebra". But, as some one
said about another subject, "Algebra has many fathers". al-Khwarizmi could be called "The
Islamic Father of Algebra", so call Diophantus "The Greek Father of Algebra". Little is known
about the life of Diophantus, except for an Algebraic Riddle quoted in The Greek Anthology,
also called Palatine Anthology, a collection of Greek epigrams, songs, 3700 short poems,
epitaphs, and rhetorical exercises. Some of the passages in The Greek Anthology resemble
epitaphs on grave stones. The passage about Diophantus presents (in translation) a riddle
about the phases of his life:
God granted him to be a boy for a sixth part of his life, and adding a twelfth part to this,
He clothed his cheeks with down; He lit him the light of wedlock after a seventh part, and five
years after his marriage He granted him a son. Alas! late-borne wretched child; after attaining
the measure of half his father's life, chill Fate took him. After consoling his grief by this
science of numbers for four years he ended his life.
Solution: Let
- x DENOTE the age at death of Diophantus;
- 1/6 x DENOTE boyhood;
- 1/12 x DENOTE youth;
- 1/7 xDENOTE batchelorhood ending in marriage;
- 5 years after marriage, a son was born;
- let 1/2 x + 4 denote the period from first fatherhood to Diophantus'
death.
- Then we have: 1/6 x + 1/12 x + 1/7 x + 5 + 1/2 x + 4 = x.
In solving, the least common denominator of these numbers (6, 12, 7, 2)
is 12 x 7 = 84. Then,
- 1/6 (84) = 14 years (boyhood);
- 1/12 (84) = 7 years (youth);
- 1/7 (84) = 12 years (batchelorhood to marriage);
- 5 years after marriage a son; son lived half of father's life, 1/2(84) = 42;
- 4 years later, death of Diophantus (apparently by suicide).
CHECKING (back to ARITHMETIC!): 14 + 7 + 12 + 5 + 42 + 4 = 21 + 17 + 46 =
38 + 46 = 84. Amswer: 84 years of life.
- directed angle
. - An angle measured from
one side (the initial side) to the other (the terminal side); often designating rotation in a
positively or negatively defined direction: for example, -45° or +20°.
- directed distance
. - For points A, B lying on a directed line, the directed distance AB
is plus or minus the distance AB, according as the direction from
A to B coincides with or is opposite that of the
directed line.
- directed graph (digraph)
. - A graph
(PL) s. t. each edge is directed ("arrowed"); simple, if no loop
(PL); complete, if edges bidrected ("doubly-arrowed"); oriented, if no
bidirection; tournament, if totally unidireted.
- directed line
. - A line on which the distance
is indicated.
- directed number
. - Label for a signed number.
- directed set
. - A partially ordered set
with ordering
 , such that every pair of elements in the set has an
upper bound. Also, labeled directed system.
, such that every pair of elements in the set has an
upper bound. Also, labeled directed system.
- directional derivative
. - To know in which
of the i, j, k directions a scalar
function may most rapidly change, we use a directional derivative which allows
choice of direction and calculation of the derivative in that direction, d(p0, p1), say, from p0(x
0, y0, z0) to p1(x1
, y1, z1). We can write a unit vector in terms of
direction cosines (PL): v = icosa +
jcosb + kcosg. Using
point coordinates, define x1 - x0

 x, y1 - y0
x, y1 - y0 
 y, z1 - z0
y, z1 - z0 
 z. The
direction is d(p0, p1) = i
z. The
direction is d(p0, p1) = i x + j
x + j y + k
y + k z; and distance
between points:
z; and distance
between points:  s = ((
s = (( x)2
+ (
x)2
+ ( y)2 + (
y)2 + ( z)2))
½. Since d(p0, p1) has the
same direction as vector v, and length equal to
z)2))
½. Since d(p0, p1) has the
same direction as vector v, and length equal to  s, then d(p0, p1)
/
s, then d(p0, p1)
/ s = v, that is, i (
s = v, that is, i ( x/
x/
 s) + y (
s) + y ( y/
y/ s) + k
(
s) + k
( z/
z/ s) = icosa + j
cosb + kcosg, or
s) = icosa + j
cosb + kcosg, or  x/
x/ s = cosa,
s = cosa,  y/
y/ s = cosb,
s = cosb,  z/
z/
 s = cosg. These direction cosines
remain constant as the distance between the two points decreases, hence, in the
limit, we have the derivatives: Dsx = cosa, Dsy = cosb, Dsz = cosg. Thus, for the function, f(x, y, z) at the
point, p(x0, y0, z0), we formally have
the derivative as the sum of partial derivatives: Dsf = f
x(x0, y0, z0)Dxf + fy(x0
, y0, z0)Dyf + fz(x0, y0,
z0)Dzf, or Dsf = fx(x0
, y0, z0)cosa + fy(x0,
y0, z0)cosb + fz(x0, y0
, z0)cosg. Part of this is found in the above
vector written in terms of unit vectors and directional cosines: v = icosa +
jcosb + kcosg. The rest
can be obtained in another vector involving our function: w = i
fx(x0, y0, z0) + jfy(x0,
y0, z0) + kfz(x0, y0, z0
)jcosb + kcosg.
Given vectors, v, w, and the result that i · i
= j · j = k · k = 1, we obtain our functional derivative as the
inner product (PL) of these two vectors: Dsf = fx(x
0, y0, z0)cosa + fy(x0
, y0, z0)cosb + fz(x0,
y0, z0)cosg = v · w = Dsf
. But what is this particular inner product? It is the gradient (PL) of the
function, f(x0, y0, z0), at point,
p(x0, y0, z0), derived via a
directional derivative, an extension of orthogonality (PL).
s = cosg. These direction cosines
remain constant as the distance between the two points decreases, hence, in the
limit, we have the derivatives: Dsx = cosa, Dsy = cosb, Dsz = cosg. Thus, for the function, f(x, y, z) at the
point, p(x0, y0, z0), we formally have
the derivative as the sum of partial derivatives: Dsf = f
x(x0, y0, z0)Dxf + fy(x0
, y0, z0)Dyf + fz(x0, y0,
z0)Dzf, or Dsf = fx(x0
, y0, z0)cosa + fy(x0,
y0, z0)cosb + fz(x0, y0
, z0)cosg. Part of this is found in the above
vector written in terms of unit vectors and directional cosines: v = icosa +
jcosb + kcosg. The rest
can be obtained in another vector involving our function: w = i
fx(x0, y0, z0) + jfy(x0,
y0, z0) + kfz(x0, y0, z0
)jcosb + kcosg.
Given vectors, v, w, and the result that i · i
= j · j = k · k = 1, we obtain our functional derivative as the
inner product (PL) of these two vectors: Dsf = fx(x
0, y0, z0)cosa + fy(x0
, y0, z0)cosb + fz(x0,
y0, z0)cosg = v · w = Dsf
. But what is this particular inner product? It is the gradient (PL) of the
function, f(x0, y0, z0), at point,
p(x0, y0, z0), derived via a
directional derivative, an extension of orthogonality (PL).
- direction angles
. - The angles between
a line in space and Cartesian coordinate axes.
- direction cosine
. - Cosine of angle
between a vector (PL) and a coordinate axis, say, v = icos
a + jcosb + kcosg
- direct product
. - PL Cartesian product
.
- direct proof
. - Proving an assertion
(PL) by deducing the desired conclusion as a logical consequence from the hypothesis and other
known or given statements.
- direct proportion
. - The relation between two functands
(PL) with contant ratio (PL antitone). Example: y = kx, for proportionality constant
k. Also labeled Also, labeled direct variation.
- directrix
. - The fixed line that, together
with a fixed point (the focus), defines a given conic; also, the (constant) ratio of the distance
from a point of the conic to the focus and the distance from that point to the directrix is the
eccentricity of the conic.
- direct search factorization
. - Simplest
prime factorization algorithm, by systematically testing trial divisors in increasing
sequence. Inefficient; used for small numbers. For a number n,
only divisors up to |_
 n_| (floor function
PL) need to be tested, since n/(|_
n_| (floor function
PL) need to be tested, since n/(|_ n_| + 1 <
n_| + 1 <  n.
n.
- direct sum
. - Given sets A, B, then
 = {a + b: a e A, b e B}. Can
extend to arbitrary number of summands.
= {a + b: a e A, b e B}. Can
extend to arbitrary number of summands.
- Dirichlet partial differential equation conditions
. - Elliptic (PL) partial differential equations (PL) are boundary value
problems requiring data to be prescribed on the boundary of the solution domain.
Dirichlet conditions prescribe the solution along the boundary domain, in contrast to
Neumann conditions (PL).
.
- Dirichlet Fourier series conditions
. - A
piecewise regular (PL) function with a finite number of finite discontinuities
and extrema can be expanded in a Fourier series (PL) converging to the
function at continuous points and and the mean of the positive-negative limits
at discontinuous points.
- Dirichlet function
. - For two distinct
real numbers, c, d (say, c = 1, d = 0,
define, D(x) = {c, for x rational; d, for x irrational}.
- discontinuity
. - A point at which a
mathematical object is discontinuous, as in a jump (PL).
- discrete set
. - A set with discrete topology
(PL), which may be induced naturally, as in the integers embedded in the real numbers.
- discrete topology
. - The topology on a
set of points such that every subset of the set is open (PL). This set and the topology
constitutes a discrete topological space.
- discrete variable
. - A functand
(PL) assuming natural number (PL) or integral (PL) values.
.
- discriminant
. - The general
quadratic equation: ax2 + bx + c = 0 has the
solution: x = (b ±
 (b2
- 4ac))/2a. Clearly, the term b2 - 4a
discriminates the type of roots of the equation -- real or complex, equal or distinct
-- hence, is labeled the discriminant of a quadratic equation. The discriminant
is an invariant of the equation: if the equation is transformed into one with other
another functand -- x -> x', the discriminant of the new
equation is simply a multiple of the former discriminat.
(b2
- 4ac))/2a. Clearly, the term b2 - 4a
discriminates the type of roots of the equation -- real or complex, equal or distinct
-- hence, is labeled the discriminant of a quadratic equation. The discriminant
is an invariant of the equation: if the equation is transformed into one with other
another functand -- x -> x', the discriminant of the new
equation is simply a multiple of the former discriminat.
- disjoint sets
. - Their union (PL)
is null.
- disjunction
. - The "or" operation in
statement logic (PL).
- disk (disc)
. - The collection of points
within a radial distance from a fixed point in Euclidean
n-space.
- dissection
. - Any two rectilinear
(PL) figures can be dissected into a finite number of pieces to form each other. (Wallace-
Bolyai-gerwein theorem.)
- distance
. - The length of a minimal path
between two given sets or geometric configurations: the distance function on two distinct two
points. For more advanced concepts PL http://www.harcourt.com/dictionary /browse/19/
- distance function
. - PL distance.
.
- distribution (generalized function)
. - The
impulse integrand, being "instaneous", is not a function, but can be represented by
a generalized function or distribution, defined as a continuous linear
functional (PL) over a space of infinitely differentiable functions s. t. each
continuous function has a g. f. derivative. (Example: Dirac's delta function, PL.) The
distribution corresponding to a function g is
T =
 W
fg.The distribution corresponding to a measure M is Tm =
W
fg.The distribution corresponding to a measure M is Tm =
 Wfd
m. Distributions differ from functions in being covariant (PL): the push
firward. Thus, given a smooth function (PL) a
: W1
Wfd
m. Distributions differ from functions in being covariant (PL): the push
firward. Thus, given a smooth function (PL) a
: W1  W
2, a distribution, W on
W1 pushes forward to a distribution on W2. On the other hand, a real function
, f, on W2
pulls back to a function, f(a(x))
, on W1. The distribution
topology (PL) is defined on the family of seminorms, NK,
a(f) = supK||Daf||
. This agrees with the C-infinity topology on copmpact subsets, wherein a
sequence converges, fn
W
2, a distribution, W on
W1 pushes forward to a distribution on W2. On the other hand, a real function
, f, on W2
pulls back to a function, f(a(x))
, on W1. The distribution
topology (PL) is defined on the family of seminorms, NK,
a(f) = supK||Daf||
. This agrees with the C-infinity topology on copmpact subsets, wherein a
sequence converges, fn  f, iff there
exists a compact set, K, s. t. all fn
are supported in K and every derivative,
Dafn converges uniformaly to Daf in K.
f, iff there
exists a compact set, K, s. t. all fn
are supported in K and every derivative,
Dafn converges uniformaly to Daf in K.
- distribution function
. - PL statistical
distribution.
- distributive lattice
. - A lattice
in which every pair of elements has an join and a meet. PL complemented distributive
lattice.
- distributive law
. - Misleading label,
dating back to Aristotle's Logic. It has persisted because of the medial operator which
became popular with the advent of printing. The label commurator law better describes it.
The concept and label operation induces the concepts and labels, operator
and operand. Thus, in the standard medial notation
2 + 4, the operator is +, the operands
are 2, 4. The prefix (a.k.a. Polish) notation
encapsulates this: +2,4. (The ordered pair notation
of set theory also encapsulates this, along with its sum:
<<2,4>,6>.) In medial notation, we have (for naturals
a,b,c): a*(b + c) = a*b + a*c. This
(passing from medial to prefix notation) becomes: a*(b+c)
-> *a+b,c and a*b + a*c ->
+*a,b,*a,c, in general, a*(b+c) =
a*b + a*c -> *a+b,c = +*a,b,*a,c, which displays operator
commuting in *+ -> +*. Hence,
commurator law is a better name than distributive law.
- divergence
. - Failure of convergence
(PL).
- divergent sequence
. - Antonomy of
convergent sequence (PL).
- divergent series
. - Antonomy of
convergent series (PL).
- divide
. - PL division.
- dividend
. - The operand of a
division operation (PL).
- division
. - Arithmetical inverse
(PL) of multiplication, defined thus (for numbers a, b,
c, with b ~= 0: a
 b = c (dividend divided
by divisor equals quotient) iff a = b*c. Division is
partial on naturals, integers, defined iff the dividend is a
natural or integral multiple of the divisor, that is, a defined quotient.
Rendering division total results in rationals, as vectors of integers
with rules derived from conserving defined
quotients.
b = c (dividend divided
by divisor equals quotient) iff a = b*c. Division is
partial on naturals, integers, defined iff the dividend is a
natural or integral multiple of the divisor, that is, a defined quotient.
Rendering division total results in rationals, as vectors of integers
with rules derived from conserving defined
quotients.
- division algrbra
. - PL division ring
.
- division algorithm
. - Given dividend
D, divisor d ~= 0, quotient Q, and remainder R, then: D = d * Q + R, where 0 </= R < d. The proviso on
remainder makes for an antitonic process (PL), which ends when remainder is less than
divisor, otherwise the division process would not end. The antitonicity of the division
algorithm makes it prototypical for every algorithm (PL).
- division ring (d. algebra, skew field)
.
- A ring (PL) in which every nonzero members has a multiplicative inverse, although
multiplication is not necessarily commutative (PL). Explicitly, a set
S(+, *) with additive associativity and commutativity and identity and inverse;
multiplicative associativity and identity and inverse; let and right ditributivity (PL
all these). In 1878 and 1880, Foebenius and Peirce proved that the only associative division
algebras are the real numbers, the complex numbers, and the quaternions.
- divisor
. - The operator of a
division operation. PL dividend.
- Dixon's factorization algorithm
. - To find
integers x, y s. t. x2
 y2 (modification of Fermat's factorization). If can, there
is a "half=half" possibility thatGCD(n, x - y) is a factor of
n. Choose randomly ri to
compute g(ri)
y2 (modification of Fermat's factorization). If can, there
is a "half=half" possibility thatGCD(n, x - y) is a factor of
n. Choose randomly ri to
compute g(ri)  r2i
mod n), and try to factor g(ri). If not easily
factorable (up to a small divisor d), try another ri, say, of form è(n)
½ø + k, k = 1, 2, ..., allowing use
of the quadratic sieve algorithm (PL). Continue finding and factoring the g(ri) until finding N d
p, where p is the prime counting function (PL).
Proceeding, for each g(ri), write g(r
i) = p1ia1ip2ia2i...pNiaNi, and form
the exponent vector:
r2i
mod n), and try to factor g(ri). If not easily
factorable (up to a small divisor d), try another ri, say, of form è(n)
½ø + k, k = 1, 2, ..., allowing use
of the quadratic sieve algorithm (PL). Continue finding and factoring the g(ri) until finding N d
p, where p is the prime counting function (PL).
Proceeding, for each g(ri), write g(r
i) = p1ia1ip2ia2i...pNiaNi, and form
the exponent vector:
æ a1i ö
ç a2i ÷
v(ri) = ç ÷
ç · ÷
ç · ÷
è aNi ø.
If aki is even for any k, then g(ri) is square, solving
x2  y2. Otherwise, search
for a linear combination (of the above matrix), Sic
iv(ri) of all even elements which "go to zero mod two", which is the
only way the problem can be solved. So, replace the aij by bij
= 0, for aij even; = 1, for a
ij odd
y2. Otherwise, search
for a linear combination (of the above matrix), Sic
iv(ri) of all even elements which "go to zero mod two", which is the
only way the problem can be solved. So, replace the aij by bij
= 0, for aij even; = 1, for a
ij odd

 2 - 1/c2ƒt2, where
c is the vacuum speed of light. In tensor notation, ¤2 f
2 - 1/c2ƒt2, where
c is the vacuum speed of light. In tensor notation, ¤2 f  (glk f;l
);l = glk ƒ
xlxkf - G ƒxl
f. (The
d'Alembertlian can more directly, and more generally, be defined in multivector theory
[31] (by variation on the multiproduct. PL) as
(glk f;l
);l = glk ƒ
xlxkf - G ƒxl
f. (The
d'Alembertlian can more directly, and more generally, be defined in multivector theory
[31] (by variation on the multiproduct. PL) as  2 - 1/u2 ƒt2, where u
has the dimension of velocity.)
2 - 1/u2 ƒt2, where u
has the dimension of velocity.) t
t  1, differentiation (PL) yields:
DtS
1, differentiation (PL) yields:
DtS m-1 (-1)m(z - a)m f(n - m)(t)f
m(a + t(z - a)), which can be integrated (PL), (A Taylor series
evolves by setting f(t - 1)n and
letting n ->
m-1 (-1)m(z - a)m f(n - m)(t)f
m(a + t(z - a)), which can be integrated (PL), (A Taylor series
evolves by setting f(t - 1)n and
letting n ->  .)
.) i
i  k, and with bi containing only those
prime factors greater than k. Then the number
i for which bi > 1 is the deficiency of
C(n, k).
k, and with bi containing only those
prime factors greater than k. Then the number
i for which bi > 1 is the deficiency of
C(n, k).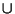 R where R is the limit of sequences of elements in S. Thus, the set of rational numbers is dense in the set of real
numbers.
R where R is the limit of sequences of elements in S. Thus, the set of rational numbers is dense in the set of real
numbers. r
r  n. These form a Grassmannian algebra (subsystem of a
Clifford algebra, PL) labled the algebra of differential forms.
n. These form a Grassmannian algebra (subsystem of a
Clifford algebra, PL) labled the algebra of differential forms. , such that every pair of elements in the set has an
upper bound. Also, labeled directed system.
, such that every pair of elements in the set has an
upper bound. Also, labeled directed system. x, y1 - y0
x, y1 - y0 

 z. The
direction is d(p0, p1) = i
z. The
direction is d(p0, p1) = i y + k
y + k z; and distance
between points:
z; and distance
between points:  s = ((
s = (( x)2
+ (
x)2
+ ( y)2 + (
y)2 + ( z)2))
½. Since d(p0, p1) has the
same direction as vector v, and length equal to
z)2))
½. Since d(p0, p1) has the
same direction as vector v, and length equal to  s, then d(p0, p1)
/
s, then d(p0, p1)
/ s = v, that is, i (
s = v, that is, i ( x/
x/
 s) + y (
s) + y ( y/
y/ s) + k
(
s) + k
( z/
z/ s) = icosa + j
cosb + kcosg, or
s) = icosa + j
cosb + kcosg, or  x/
x/ s = cosa,
s = cosa,  y/
y/ s = cosb,
s = cosb,  z/
z/
 s = cosg. These direction cosines
remain constant as the distance between the two points decreases, hence, in the
limit, we have the derivatives: Dsx = cosa, Dsy = cosb, Dsz = cosg. Thus, for the function, f(x, y, z) at the
point, p(x0, y0, z0), we formally have
the derivative as the sum of partial derivatives: Dsf = f
x(x0, y0, z0)Dxf + fy(x0
, y0, z0)Dyf + fz(x0, y0,
z0)Dzf, or Dsf = fx(x0
, y0, z0)cosa + fy(x0,
y0, z0)cosb + fz(x0, y0
, z0)cosg. Part of this is found in the above
vector written in terms of unit vectors and directional cosines: v = icosa +
jcosb + kcosg. The rest
can be obtained in another vector involving our function: w = i
fx(x0, y0, z0) + jfy(x0,
y0, z0) + kfz(x0, y0, z0
)jcosb + kcosg.
Given vectors, v, w, and the result that i · i
= j · j = k · k = 1, we obtain our functional derivative as the
inner product (PL) of these two vectors: Dsf = fx(x
0, y0, z0)cosa + fy(x0
, y0, z0)cosb + fz(x0,
y0, z0)cosg = v · w = Dsf
. But what is this particular inner product? It is the gradient (PL) of the
function, f(x0, y0, z0), at point,
p(x0, y0, z0), derived via a
directional derivative, an extension of orthogonality (PL).
s = cosg. These direction cosines
remain constant as the distance between the two points decreases, hence, in the
limit, we have the derivatives: Dsx = cosa, Dsy = cosb, Dsz = cosg. Thus, for the function, f(x, y, z) at the
point, p(x0, y0, z0), we formally have
the derivative as the sum of partial derivatives: Dsf = f
x(x0, y0, z0)Dxf + fy(x0
, y0, z0)Dyf + fz(x0, y0,
z0)Dzf, or Dsf = fx(x0
, y0, z0)cosa + fy(x0,
y0, z0)cosb + fz(x0, y0
, z0)cosg. Part of this is found in the above
vector written in terms of unit vectors and directional cosines: v = icosa +
jcosb + kcosg. The rest
can be obtained in another vector involving our function: w = i
fx(x0, y0, z0) + jfy(x0,
y0, z0) + kfz(x0, y0, z0
)jcosb + kcosg.
Given vectors, v, w, and the result that i · i
= j · j = k · k = 1, we obtain our functional derivative as the
inner product (PL) of these two vectors: Dsf = fx(x
0, y0, z0)cosa + fy(x0
, y0, z0)cosb + fz(x0,
y0, z0)cosg = v · w = Dsf
. But what is this particular inner product? It is the gradient (PL) of the
function, f(x0, y0, z0), at point,
p(x0, y0, z0), derived via a
directional derivative, an extension of orthogonality (PL). n_| (floor function
PL) need to be tested, since n/(|_
n_| (floor function
PL) need to be tested, since n/(|_ n_| + 1 <
n_| + 1 <  n.
n. = {a + b: a e A, b e B}. Can
extend to arbitrary number of summands.
= {a + b: a e A, b e B}. Can
extend to arbitrary number of summands. (b2
- 4ac))/2a. Clearly, the term b2 - 4a
discriminates the type of roots of the equation -- real or complex, equal or distinct
-- hence, is labeled the discriminant of a quadratic equation. The discriminant
is an invariant of the equation: if the equation is transformed into one with other
another functand -- x -> x', the discriminant of the new
equation is simply a multiple of the former discriminat.
(b2
- 4ac))/2a. Clearly, the term b2 - 4a
discriminates the type of roots of the equation -- real or complex, equal or distinct
-- hence, is labeled the discriminant of a quadratic equation. The discriminant
is an invariant of the equation: if the equation is transformed into one with other
another functand -- x -> x', the discriminant of the new
equation is simply a multiple of the former discriminat. W
fg
W
fg Wfd
m. Distributions differ from functions in being covariant (PL): the push
firward. Thus, given a smooth function (PL) a
: W1
Wfd
m. Distributions differ from functions in being covariant (PL): the push
firward. Thus, given a smooth function (PL) a
: W1  W
2, a distribution, W on
W1 pushes forward to a distribution on W2. On the other hand, a real function
, f, on W2
pulls back to a function, f(a(x))
, on W1. The distribution
topology (PL) is defined on the family of seminorms, NK,
a(f) = supK||Daf||
. This agrees with the C-infinity topology on copmpact subsets, wherein a
sequence converges, fn
W
2, a distribution, W on
W1 pushes forward to a distribution on W2. On the other hand, a real function
, f, on W2
pulls back to a function, f(a(x))
, on W1. The distribution
topology (PL) is defined on the family of seminorms, NK,
a(f) = supK||Daf||
. This agrees with the C-infinity topology on copmpact subsets, wherein a
sequence converges, fn  f, iff there
exists a compact set, K, s. t. all fn
are supported in K and every derivative,
Dafn converges uniformaly to Daf in K.
f, iff there
exists a compact set, K, s. t. all fn
are supported in K and every derivative,
Dafn converges uniformaly to Daf in K. b = c (dividend divided
by divisor equals quotient) iff a = b*c. Division is
partial on naturals, integers, defined iff the dividend is a
natural or integral multiple of the divisor, that is, a defined quotient.
Rendering division total results in rationals, as vectors of integers
with rules derived from conserving defined
quotients.
b = c (dividend divided
by divisor equals quotient) iff a = b*c. Division is
partial on naturals, integers, defined iff the dividend is a
natural or integral multiple of the divisor, that is, a defined quotient.
Rendering division total results in rationals, as vectors of integers
with rules derived from conserving defined
quotients. y2 (modification of Fermat's factorization). If can, there
is a "half=half" possibility thatGCD(n, x - y) is a factor of
n. Choose randomly ri to
compute g(ri)
y2 (modification of Fermat's factorization). If can, there
is a "half=half" possibility thatGCD(n, x - y) is a factor of
n. Choose randomly ri to
compute g(ri)  r2i
mod n), and try to factor g(ri). If not easily
factorable (up to a small divisor d), try another ri, say, of form è(n)
½ø + k, k = 1, 2, ..., allowing use
of the quadratic sieve algorithm (PL). Continue finding and factoring the g(ri) until finding N
r2i
mod n), and try to factor g(ri). If not easily
factorable (up to a small divisor d), try another ri, say, of form è(n)
½ø + k, k = 1, 2, ..., allowing use
of the quadratic sieve algorithm (PL). Continue finding and factoring the g(ri) until finding N  y2. Otherwise, search
for a linear combination (of the above matrix), Sic
iv(ri) of all even elements which "go to zero mod two", which is the
only way the problem can be solved. So, replace the aij by bij
= 0, for aij even; = 1, for a
ij odd
y2. Otherwise, search
for a linear combination (of the above matrix), Sic
iv(ri) of all even elements which "go to zero mod two", which is the
only way the problem can be solved. So, replace the aij by bij
= 0, for aij even; = 1, for a
ij odd