E
_________________________________________________________________________________________________
- eccentric angle
. - Angle measured at the
center of an ellipse (or hyperbola) from the line passing through the foci to the line from the
center to a point on the ellipse (or hyperbola). Equivalently the angle q
that appears in the parametric equations of the ellipse or hyperbola in normal form; namely,
x = a cos q, y = b sin
q or x = a sec q, y = b tan q, respectively.
- eccentricity
. - Measure, e,on a conic section (PL) in terms of semimajor, semiminor axes (PL).
Equivalently, fraction of distance to semimajor axis as which focus (PL) lies. For
circle: e = 0; ellipse: 0 < e < 1
; parabola: e = 1; hyperbola: e
> 1.
- edge
. - A boundary of a plane geometric
figure. A straight line intersecting two faces of a solid figure. For edge in graph
theory PL http://www.harcourt.com/dictionary /browse/19//
- Egyptian fractions
. - Ancient
Egyptians calculated by unit fractions, such as 1/2, 1/3, 1/4, 1/10, .... The
hieroglyph for an open mouth was used to DENOTE A FRACTION, with a number
hieroglyph written below this "open mouth" icon to DENOTE DENOMINATOR OF
THE FRACTION. Any FRACTION we write with a non-UNIT NUMERATOR was
written by ancient Egyptians as a SUM OF UNIT FRACTIONS. These UNIT FRACTIONS
have, therefore, become known as "Egyptian Fractions". We use them every day
in making change for a dollar: 1 penny => $1/100; 1 nickel => $1/20;
1 dime => $1/10; 1 quarter => $1/4; 1 half-dollar => $1/2. The
great British mathematician, J. J. Sylvester (1814-197) -- once the tutor of
the young Florence Nightingale -- developed AN ALGORITHM FOR CONVERTING ANY
NON-UNIT FRACTION TO THE SUM OF UNIT OR EQYPTIAN FRACTIONS.
- Given a fraction, such as 7/24, find the LARGEST EGYPTIAN FRACTION JUST
LESS than 7/24.
- Find this by performing DIVISION: 24
 7 = 3 + REMAINDER 3. So 1/4 = 6/24 is the ANSWER.
7 = 3 + REMAINDER 3. So 1/4 = 6/24 is the ANSWER.
- Perform SUBTRACTION: 7/24 - 1/4 = 7/24 - 6/24 = 1/24.
- Hence, 7/24 = 1/4 + 1/24.
Again,
- Given 2/35, find the LARGEST EGYPTIAN FRACTION JUST LESS than 2/35.
- DIVISION: 35
 2 = 17 + REMAINDER 1. So 1/18 is the ANSWER.
2 = 17 + REMAINDER 1. So 1/18 is the ANSWER.
- 2/35 - 1/18 = (2 · 18)/(35 · 18) - (1 · 35)/(18 · 35)
= 36/630 - 35/360 = 1/360.
- Hence, 2/35 = 1/18 + 1/630.
Etc.
eigenfunction. PL proper fnction
eigenmatrix. PL proper matrix.
eigenspace. PL proper space..
eigenvalue. PL proper value.
eigenvector. PL proper vector..
Einstein-Lorentz group (Lorentz group).
The time-preserving group of isometries of Minkowski space (PL) with
pseudo-Riemannian metric (PL): dt2 =
- dt2 + dx2 + dy2 + dz2. Equivalently, the
isometries of 3-D hyperbolic space (Pl). (time-preserving: the time vector
(1, 0, 0, 0)  (t, x, y, z), t > 0).
equipollent. An equivalence of
statements, sets, etc.
element A set member. In analysis, the
integrand (PL) of a definite integral. Also, an element of arc length approximating the
length of a curve between two points; an element in the planar region bounded by a curve or the
volume of region in space; an entry aij of a matrix, located
at the intersection of the ith row and jth
column of the matrix. More generally, a fundamental assumption or proposition of geometry,
calculus, or other field.
eliminant. Given a system of two
homogeneous linear equations (PL) in two independent functands (PL, say x,y). Application of the elimination algorithm to this system results in
one equation in one functand which can easily be solved for that functand, which can then
used to solve for the other. The elimination centers around the determinant of the matrix of
coefficients of the system, a determinant known as the eliminant. (The process can be
applied to a system of three equations, but becomes difficult for larger systems.) If the eliminant
equals zero, the equations are interdependent, and the elimination algorithm fails.
The elimination algorithm is thought to go back to a Chinese mathematician of the 10th
century AD. The eliminant inspired the development of matrix algebra, a powerful
field of mathematics -- created by the British mathematican, Arthur Cayley (1821-1895).
elimination. PL eliminant.
ellipse. A planar curve (PL) whose
locus (PL) consists of all points such that the sum of the distance to two fixed points
(foci) is constant. (The ellipse is classified as a conic whose eccentricity
(PL) is less than 1. The Greek mathematician xxxx (x-y) demonstrated that a conic is the closed
conic section obtained by intersecting a cone with some planes not parallel to a generator of the
cone.) A general elliptic equation is Ax2 + 2Bxy + Cy2 +
2Dx + 2Ey + F = 0, where its disciminant (PL), AC - B2
> 0; in normal form (with foci symmetrically placed on the coordinate axes about
the origin), this equation takes the form, x2/a2 + y
2/b2 = 1. The circle is an ellipse, in the special case that
a = b.
ellipsoid. A smooth closed surface, whose
planar sections are ellipses (PL). Equivalently, a solution surface (PL) of a
general quadratic equation, Ax2 + 2Bxy + 2Cxz + Dy2 +
2Eyz + Fz2 + 2Gx + 2Hy + 2Iz + J = 0, in 3-D whose Hessian (PL) (in this
case, a matrix of constants) has a positive determinant (PL). The simplest ellipsoid
has the equation, x2/a2 + y2/b>2
+ z2/c2 = 1. If at least two of <parameters (PL), a, b,c are equal, then the surface is an ellipsoid of revolution (PL), formed
by rotating an ellipse about one of its axes. The plane sections perpendicular to the
axis of rotation are circles. The sphere is an ellipsoid, in the special case that parameters
a = b = c = 1. Also, the solid enclosed by such a surface.
elliptic coordinates (ellipsoidal c., confocal e. c.)
. Given by equations: x2/(a2 + x) + y2/(b2 + x) + z2
/(c2 + x), x2/(a2 + h) + y2/(b2 + h) + z2
/(c2 + h), x2/(a2 +
z) + y2/(b2 + z) + z2/(c2
+ z), where -c2 < x <
(t, x, y, z), t > 0).
equipollent. An equivalence of
statements, sets, etc.
element A set member. In analysis, the
integrand (PL) of a definite integral. Also, an element of arc length approximating the
length of a curve between two points; an element in the planar region bounded by a curve or the
volume of region in space; an entry aij of a matrix, located
at the intersection of the ith row and jth
column of the matrix. More generally, a fundamental assumption or proposition of geometry,
calculus, or other field.
eliminant. Given a system of two
homogeneous linear equations (PL) in two independent functands (PL, say x,y). Application of the elimination algorithm to this system results in
one equation in one functand which can easily be solved for that functand, which can then
used to solve for the other. The elimination centers around the determinant of the matrix of
coefficients of the system, a determinant known as the eliminant. (The process can be
applied to a system of three equations, but becomes difficult for larger systems.) If the eliminant
equals zero, the equations are interdependent, and the elimination algorithm fails.
The elimination algorithm is thought to go back to a Chinese mathematician of the 10th
century AD. The eliminant inspired the development of matrix algebra, a powerful
field of mathematics -- created by the British mathematican, Arthur Cayley (1821-1895).
elimination. PL eliminant.
ellipse. A planar curve (PL) whose
locus (PL) consists of all points such that the sum of the distance to two fixed points
(foci) is constant. (The ellipse is classified as a conic whose eccentricity
(PL) is less than 1. The Greek mathematician xxxx (x-y) demonstrated that a conic is the closed
conic section obtained by intersecting a cone with some planes not parallel to a generator of the
cone.) A general elliptic equation is Ax2 + 2Bxy + Cy2 +
2Dx + 2Ey + F = 0, where its disciminant (PL), AC - B2
> 0; in normal form (with foci symmetrically placed on the coordinate axes about
the origin), this equation takes the form, x2/a2 + y
2/b2 = 1. The circle is an ellipse, in the special case that
a = b.
ellipsoid. A smooth closed surface, whose
planar sections are ellipses (PL). Equivalently, a solution surface (PL) of a
general quadratic equation, Ax2 + 2Bxy + 2Cxz + Dy2 +
2Eyz + Fz2 + 2Gx + 2Hy + 2Iz + J = 0, in 3-D whose Hessian (PL) (in this
case, a matrix of constants) has a positive determinant (PL). The simplest ellipsoid
has the equation, x2/a2 + y2/b>2
+ z2/c2 = 1. If at least two of <parameters (PL), a, b,c are equal, then the surface is an ellipsoid of revolution (PL), formed
by rotating an ellipse about one of its axes. The plane sections perpendicular to the
axis of rotation are circles. The sphere is an ellipsoid, in the special case that parameters
a = b = c = 1. Also, the solid enclosed by such a surface.
elliptic coordinates (ellipsoidal c., confocal e. c.)
. Given by equations: x2/(a2 + x) + y2/(b2 + x) + z2
/(c2 + x), x2/(a2 + h) + y2/(b2 + h) + z2
/(c2 + h), x2/(a2 +
z) + y2/(b2 + z) + z2/(c2
+ z), where -c2 < x <  , -b2 < h <
-c2, -a2 < z < -b2.
elliptic (Riemannian) geometry. A
constant curvature nonEuclidean (PL) geometry replacing the parallel postulate
of Euclidean geometry (PL) (a.k.a. parabolic geometry, PL) with statement "through
any planar point, there exists no line parallel to a given line". Other postulates or axioms are
modified for consistency. Geometry can be visualized on a sphere, with great circles
as "lines". (Applied in Einstein's General Theory of Rlativity. PL hyperbolic
geometry .)
elliptic umbilic catastrophe. PL
catastrophe.
embedding. Representing a topological
object so as to preserve its connectivity or algebraic properties.
empirical curve. Curve fitting a set of
observed data.
empty set. The set containing no members,
denoted { } =
, -b2 < h <
-c2, -a2 < z < -b2.
elliptic (Riemannian) geometry. A
constant curvature nonEuclidean (PL) geometry replacing the parallel postulate
of Euclidean geometry (PL) (a.k.a. parabolic geometry, PL) with statement "through
any planar point, there exists no line parallel to a given line". Other postulates or axioms are
modified for consistency. Geometry can be visualized on a sphere, with great circles
as "lines". (Applied in Einstein's General Theory of Rlativity. PL hyperbolic
geometry .)
elliptic umbilic catastrophe. PL
catastrophe.
embedding. Representing a topological
object so as to preserve its connectivity or algebraic properties.
empirical curve. Curve fitting a set of
observed data.
empty set. The set containing no members,
denoted { } = 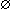 . Also, labeled null set.
endogenous functand. A dependent functand
(PL); a functand that is inherently part of a mathematical model (PL), such as the cost
of labor or material in a profit model.
endomorphism. A homomorphic map (PL) of an
algebraic object (such as a group or a ring) to itself.
end point. Boundary point of an interval, line
segment, or arc.
ensemble. An infinity of fictitious
alternate universes in a stochastic process (PL).
ensemble average. A stochastic average
(PL) taken over an infinity of fictitious alternate universes called ensemble. In each
member of the ensemble, the stochastic process is imagined to experience different random transformations.
The resulting average is the expected value of the quantity, usually expressed as an
integral over the probability density function of the stochastic process. For example, the
expected value of a coin toss (heads = 1, tails = 0) is 1/2,
even though such a result will never occur and can hardly be "expected." (This is a figure&ground
strategy, comparable to using the normal distribution as a figure, since a marginal
deviation from it is statistically significant.) The ensemble average is conceptually distinct from
the time average. If the two averages coincide, the process is ergodic (PL).
entire function. A complex function
(PL) which is analytic (PL) at all points of the complex plane (PL).
Examples: exponential (PL); sine (PL); cosine (PL); etc.
enumerable. Countable. Every finite
set is, of course, enumerable. An infinite set (such as the rational numbers)
is enumerable iff one-one correspondent with the set of intgers.
enumerable set. Pl enumerable.
envelope of a family of curves. A curve
whose every point is tangent to a member of a family of curves.
epicycle. The path a circle would make if it rolled around
the circumference of another circle such that a fixed point on the "moving" circle would trace out an
epicycloid (PL). (Such epicycles are observed in the path of the planet Mars causing the Ptolemaic
explanation of "the universe" -- in which the sun encircled the Earth - and were post facto afixed to the
"circle orbit" of the planet. Once the "Coperican" model was adopted, these epicycles were explained by Earth's
passing Mars -- a phenomenon which any nondriving passenger can observe when riding in a car that passes
another one on the highway.)
epicycloid. PL epicycle.
epitrochoid. The roulette traced
by a point fixed on a circle which rolls around the outside of a larger circle.
equal. A relation between two or more quantities having
the same value or contextually considered the same. The numerical case of an equivalence relation (PL).
equality. Label for an equivalence relation (PL),
which is any relation that is reflexive, symmetric, transitive (PL). For significance in advanced set theory
or foundations of mathematics PL http://www.harcourt.com/dictionary /browse/19/.
equalizer. The equalizer of two maps
(PL), f, g:X
. Also, labeled null set.
endogenous functand. A dependent functand
(PL); a functand that is inherently part of a mathematical model (PL), such as the cost
of labor or material in a profit model.
endomorphism. A homomorphic map (PL) of an
algebraic object (such as a group or a ring) to itself.
end point. Boundary point of an interval, line
segment, or arc.
ensemble. An infinity of fictitious
alternate universes in a stochastic process (PL).
ensemble average. A stochastic average
(PL) taken over an infinity of fictitious alternate universes called ensemble. In each
member of the ensemble, the stochastic process is imagined to experience different random transformations.
The resulting average is the expected value of the quantity, usually expressed as an
integral over the probability density function of the stochastic process. For example, the
expected value of a coin toss (heads = 1, tails = 0) is 1/2,
even though such a result will never occur and can hardly be "expected." (This is a figure&ground
strategy, comparable to using the normal distribution as a figure, since a marginal
deviation from it is statistically significant.) The ensemble average is conceptually distinct from
the time average. If the two averages coincide, the process is ergodic (PL).
entire function. A complex function
(PL) which is analytic (PL) at all points of the complex plane (PL).
Examples: exponential (PL); sine (PL); cosine (PL); etc.
enumerable. Countable. Every finite
set is, of course, enumerable. An infinite set (such as the rational numbers)
is enumerable iff one-one correspondent with the set of intgers.
enumerable set. Pl enumerable.
envelope of a family of curves. A curve
whose every point is tangent to a member of a family of curves.
epicycle. The path a circle would make if it rolled around
the circumference of another circle such that a fixed point on the "moving" circle would trace out an
epicycloid (PL). (Such epicycles are observed in the path of the planet Mars causing the Ptolemaic
explanation of "the universe" -- in which the sun encircled the Earth - and were post facto afixed to the
"circle orbit" of the planet. Once the "Coperican" model was adopted, these epicycles were explained by Earth's
passing Mars -- a phenomenon which any nondriving passenger can observe when riding in a car that passes
another one on the highway.)
epicycloid. PL epicycle.
epitrochoid. The roulette traced
by a point fixed on a circle which rolls around the outside of a larger circle.
equal. A relation between two or more quantities having
the same value or contextually considered the same. The numerical case of an equivalence relation (PL).
equality. Label for an equivalence relation (PL),
which is any relation that is reflexive, symmetric, transitive (PL). For significance in advanced set theory
or foundations of mathematics PL http://www.harcourt.com/dictionary /browse/19/.
equalizer. The equalizer of two maps
(PL), f, g:X  Y in a category (PL) is an
inxlusion map (PL) e:E
Y in a category (PL) is an
inxlusion map (PL) e:E  X s.t. (composition)
f o e= g o e; any other map with the same property fits with the
inclusion map and an identity map in a commutative diagram (PL). The equalizer is a
monomorphism (PL), unique up to isomorphism (PL). In the category of sets,
the equalizer is given by the set, E = {e e x: f(x) =
g(x)} and by the above inclusion map. The dual (PL) is coequalizer.
equal sets. PL equipollent..
equate. Set the forms equal to each
other.
equation. Standard form: A symbolic
statement with operations on one side, with zero on the other..
equiangular. Geometric angles which are
equal in measure..
equiangular polygon. A polygon
all of whose angles are equal. Also labeled regular polygon.
equidistant. PL standard dictionary.
equilateral. PL standard dictionary.
equilateral polygon. Polygon whose
angles are equal.
equilateral polyhedron. Polyhedron whose
angles are equal.
equipotent sets. In standard
set theory (PL t-set theory), sets are equipotent iff they have the same
members. (PL extollence)..
equivalence. PL relation,
equivalence.
equivalence classes. PL relation,
equivalence.
equivalence relation. PL relation,
equivalence.
equivalent. The relata
of an equivalence relation PL.
equivalent sets. In standard
set theory (PL t-set theory), two sets are equivalent iff they have the
same members. This is equipollence (PL equipotent sets, also extollence for o-sets)..
erect. PL standard dictionary.
ergodic. Concerning a process s.
t. any "sizable sample" represents the whole, regarding a specific statistical parameter.
ergodic measure. An endomorphism
(PL) on a set, S, s. t., if it is invariant under transFormation, then
the measure is either m(S) = 0 or m(S) = 1.
ergodic theory. The study of statistical
and qualitative group-semigroup action (PL) on measure spaces (PL).
ergodic transformation. Has only
trivially invariant subsets.
essential singularity. A singular
point (PL), p, for which f(z)(z - p)n
is not differentiable for any n > 0.
essential supremum. Given R, a measure space (PL), X with measure (PL) m, and a measurable function
(PL), f:X
X s.t. (composition)
f o e= g o e; any other map with the same property fits with the
inclusion map and an identity map in a commutative diagram (PL). The equalizer is a
monomorphism (PL), unique up to isomorphism (PL). In the category of sets,
the equalizer is given by the set, E = {e e x: f(x) =
g(x)} and by the above inclusion map. The dual (PL) is coequalizer.
equal sets. PL equipollent..
equate. Set the forms equal to each
other.
equation. Standard form: A symbolic
statement with operations on one side, with zero on the other..
equiangular. Geometric angles which are
equal in measure..
equiangular polygon. A polygon
all of whose angles are equal. Also labeled regular polygon.
equidistant. PL standard dictionary.
equilateral. PL standard dictionary.
equilateral polygon. Polygon whose
angles are equal.
equilateral polyhedron. Polyhedron whose
angles are equal.
equipotent sets. In standard
set theory (PL t-set theory), sets are equipotent iff they have the same
members. (PL extollence)..
equivalence. PL relation,
equivalence.
equivalence classes. PL relation,
equivalence.
equivalence relation. PL relation,
equivalence.
equivalent. The relata
of an equivalence relation PL.
equivalent sets. In standard
set theory (PL t-set theory), two sets are equivalent iff they have the
same members. This is equipollence (PL equipotent sets, also extollence for o-sets)..
erect. PL standard dictionary.
ergodic. Concerning a process s.
t. any "sizable sample" represents the whole, regarding a specific statistical parameter.
ergodic measure. An endomorphism
(PL) on a set, S, s. t., if it is invariant under transFormation, then
the measure is either m(S) = 0 or m(S) = 1.
ergodic theory. The study of statistical
and qualitative group-semigroup action (PL) on measure spaces (PL).
ergodic transformation. Has only
trivially invariant subsets.
essential singularity. A singular
point (PL), p, for which f(z)(z - p)n
is not differentiable for any n > 0.
essential supremum. Given R, a measure space (PL), X with measure (PL) m, and a measurable function
(PL), f:X  R
, then the essential supremum is least number, n,
s.t. the set, {x: f(x) > n}, has measure zero (PL). If no such
number exists -- as for f(x) = 1/x on open set, (0, 1)
, then the essential supremum is
R
, then the essential supremum is least number, n,
s.t. the set, {x: f(x) > n}, has measure zero (PL). If no such
number exists -- as for f(x) = 1/x on open set, (0, 1)
, then the essential supremum is  . The essential supremum of the
absolute value of a function, ||f||
. The essential supremum of the
absolute value of a function, ||f|| provides the norm for L-infinity-space.
Etale space. Arising from a sheaf
(PL) of continuous functions, with a natural topology (PL) due to the projection operator
(PL). (Etale spaces are not Hausdorff spacee, PL.)
Euclidean algorithm. For determining
the greatest common divisor (GCD) of two numbers (PL). (1)Divide the lesser
into the greater; (2)if the remainder is 0, the divisor is the GCD of the two numbers, otherwise
divide the remainder into the divisor of the previous stage. Clearly, this
recursively continues until a divisor yields a 0 remainder, indentifying
the associated divisor as the GCD of the two numbers. To find the GCD of more
than two numbers, find the GCD of two of them; compound this with a third, to
find their GCD; etc. The Euclidean algorithm is a subalgorithm of
the algorithm for finding the least common multiple (LCM) (PL)
of two or more numbers. Students of computer science know that
the simple programming of the Euclidean algorithm lends itself to testing the
speed of functioning of the logic circuits (PL) of a given
computer.
Euclidean domain. PL Euclidean ring
.
Euclidean geometry. The set of all
properties invariant under the Euclidean group.
Euclidean group. The equivalence
relation (PL) in Euclidean geometry is congruence: perfect matching
of structure. Not every transformation on a structure in Euclidean geometry leaves the
structure invariant, but may distort it in shape (angle or length),
so that congruent structures may depart from congruence after transformation.
But the transformations of translation, rotation, reflection (PL)
maintain any existing congruence. Their "functional addition" (one transformation
followed by, or concatenated with, another of the three transformations) is equivalent to a
member of the transformation set (closure); also, the inverse of any one of these three
transformations is one of the three transformations, hence, these three transformations
and their concatenations form the Euclidean group. (Actually it has been shown [12]
that Euclidean geometry can be reduced to the single transformation of reflection, hence,
the Euclidean group is thereby reduced. Why isn't this generally known and widely
taught?)
Euclidean ring. A ring (PL) w. o.
zero divisors allowing the Euclidean algorithm (PL) and an integer norm
(PL).
Euler angles. According to
Euler's rotation theorem (PL), any rotation may be encapsulated in terms of exactly
three angles (f, q, y). (PL Euler angles.) The literature
records many conventions for the Euler angles, involving the axes for the rotation.
Perhaps "standard" is the "x-convention", so-called because the first-f
and third-y rotations are about the x-axis of a 3-D ccordination (the second-q about the
z-axis of this coordination). Each of the three rotations may be
represented by a 3 X 3 matrix, labeled, respectively, as (say)
O, P, Q, so that the general rotation is their matrix product
: R = OPQ. Components: o11 = cos f, o12 = sin f
, o13 = 0, o21 = -sin
f, o22 = cos f
, o31 =
0, o32= 0, o33 = 1
; p11 = 1, p12 = 0
, p13 = 0, p21 = cos
q, p22 = -sin q
, p23 = 0, p31 = 0
, p32= -sin q, p33 = cos q; with q the
same as B after substitution
f
provides the norm for L-infinity-space.
Etale space. Arising from a sheaf
(PL) of continuous functions, with a natural topology (PL) due to the projection operator
(PL). (Etale spaces are not Hausdorff spacee, PL.)
Euclidean algorithm. For determining
the greatest common divisor (GCD) of two numbers (PL). (1)Divide the lesser
into the greater; (2)if the remainder is 0, the divisor is the GCD of the two numbers, otherwise
divide the remainder into the divisor of the previous stage. Clearly, this
recursively continues until a divisor yields a 0 remainder, indentifying
the associated divisor as the GCD of the two numbers. To find the GCD of more
than two numbers, find the GCD of two of them; compound this with a third, to
find their GCD; etc. The Euclidean algorithm is a subalgorithm of
the algorithm for finding the least common multiple (LCM) (PL)
of two or more numbers. Students of computer science know that
the simple programming of the Euclidean algorithm lends itself to testing the
speed of functioning of the logic circuits (PL) of a given
computer.
Euclidean domain. PL Euclidean ring
.
Euclidean geometry. The set of all
properties invariant under the Euclidean group.
Euclidean group. The equivalence
relation (PL) in Euclidean geometry is congruence: perfect matching
of structure. Not every transformation on a structure in Euclidean geometry leaves the
structure invariant, but may distort it in shape (angle or length),
so that congruent structures may depart from congruence after transformation.
But the transformations of translation, rotation, reflection (PL)
maintain any existing congruence. Their "functional addition" (one transformation
followed by, or concatenated with, another of the three transformations) is equivalent to a
member of the transformation set (closure); also, the inverse of any one of these three
transformations is one of the three transformations, hence, these three transformations
and their concatenations form the Euclidean group. (Actually it has been shown [12]
that Euclidean geometry can be reduced to the single transformation of reflection, hence,
the Euclidean group is thereby reduced. Why isn't this generally known and widely
taught?)
Euclidean ring. A ring (PL) w. o.
zero divisors allowing the Euclidean algorithm (PL) and an integer norm
(PL).
Euler angles. According to
Euler's rotation theorem (PL), any rotation may be encapsulated in terms of exactly
three angles (f, q, y). (PL Euler angles.) The literature
records many conventions for the Euler angles, involving the axes for the rotation.
Perhaps "standard" is the "x-convention", so-called because the first-f
and third-y rotations are about the x-axis of a 3-D ccordination (the second-q about the
z-axis of this coordination). Each of the three rotations may be
represented by a 3 X 3 matrix, labeled, respectively, as (say)
O, P, Q, so that the general rotation is their matrix product
: R = OPQ. Components: o11 = cos f, o12 = sin f
, o13 = 0, o21 = -sin
f, o22 = cos f
, o31 =
0, o32= 0, o33 = 1
; p11 = 1, p12 = 0
, p13 = 0, p21 = cos
q, p22 = -sin q
, p23 = 0, p31 = 0
, p32= -sin q, p33 = cos q; with q the
same as B after substitution
f  y; so that the product rotation
is r11 = cos y cos
f - cos q sin y sin f
, r21 = cos y cos f + cos q sin y sin f, r13 = sin y sin
q, r21 = - sin y
cos f - cos q sin f
cos y, r22 = - sin y cos f + cos q sin fcos y, r23 =
cos y sin q, r31
= sin q sin f,
r32 = - sin q cos f, r33 = cos q. For computational purposes,
instead of Euler angles, the general rotation is obtained via the Euler
parameters (PL).
Eulerian numbers. PL Euler numbers
.
Eulerian trail. A walk (a.k.a.
traversal) of a graph (PL) which traverses each edge exactly once. A
connected graph (PL) is an Eulerian trail iff having at most two vertices of odd
degree (PL). (PL Eulerian connection, Eulerian graph, Könisberg bridge problem
.).
Euler four-square identity. Communicated
by Euler to Goldbach (1690-1764) in a 1750 letter: (a12 +
a22 + a32 + a42) (b1
2 + b22 + b32 + b42)
= (a1b1 - a2b2 - a3b3 - a
4b4)2 + (a1b2 + a2b1 +
a3b4 - a4b3)2 + (a1b3
- a2b4 + a3b1 + a4b2)
2+ (a1b4 + a2b3 - a3b2
a4b1)2.
Euler numbers. PL alternating
permutation.
Euler parameters. In terms of the (PL), the parameters are: e
0 = cos[½(f + y)]cos(½
q); e1 =
sin[½(f - y)]sin(½q); e2 = cos[½
(f - y)]sin(½q)
; e3 = sin[½(f + y)]cos(½q).
This forms a quaternion (PL), (e0,
e) = e0 + e1i + e2j + e3k, where i2 = j2 = k2 = - 1, but i
y; so that the product rotation
is r11 = cos y cos
f - cos q sin y sin f
, r21 = cos y cos f + cos q sin y sin f, r13 = sin y sin
q, r21 = - sin y
cos f - cos q sin f
cos y, r22 = - sin y cos f + cos q sin fcos y, r23 =
cos y sin q, r31
= sin q sin f,
r32 = - sin q cos f, r33 = cos q. For computational purposes,
instead of Euler angles, the general rotation is obtained via the Euler
parameters (PL).
Eulerian numbers. PL Euler numbers
.
Eulerian trail. A walk (a.k.a.
traversal) of a graph (PL) which traverses each edge exactly once. A
connected graph (PL) is an Eulerian trail iff having at most two vertices of odd
degree (PL). (PL Eulerian connection, Eulerian graph, Könisberg bridge problem
.).
Euler four-square identity. Communicated
by Euler to Goldbach (1690-1764) in a 1750 letter: (a12 +
a22 + a32 + a42) (b1
2 + b22 + b32 + b42)
= (a1b1 - a2b2 - a3b3 - a
4b4)2 + (a1b2 + a2b1 +
a3b4 - a4b3)2 + (a1b3
- a2b4 + a3b1 + a4b2)
2+ (a1b4 + a2b3 - a3b2
a4b1)2.
Euler numbers. PL alternating
permutation.
Euler parameters. In terms of the (PL), the parameters are: e
0 = cos[½(f + y)]cos(½
q); e1 =
sin[½(f - y)]sin(½q); e2 = cos[½
(f - y)]sin(½q)
; e3 = sin[½(f + y)]cos(½q).
This forms a quaternion (PL), (e0,
e) = e0 + e1i + e2j + e3k, where i2 = j2 = k2 = - 1, but i
 j
j  k
k  i, and ij =
k, jk = i, ki = j. Using the parameters, the rotation formula becomes: r' = r(e02 - e
12 - e22 - e
3) + 2e(e · r) + (r X normal)sinf.
Euler phi function. PL totient
function.
Euler polynomial. Appears in Appell
sequence (PL) where g(t) = ½(et + 1) for
generating functiom (PL), (2ext)/(er + 1)
i, and ij =
k, jk = i, ki = j. Using the parameters, the rotation formula becomes: r' = r(e02 - e
12 - e22 - e
3) + 2e(e · r) + (r X normal)sinf.
Euler phi function. PL totient
function.
Euler polynomial. Appears in Appell
sequence (PL) where g(t) = ½(et + 1) for
generating functiom (PL), (2ext)/(er + 1)  S
S n=0En
tn/n!. The Euler polynomials are related to the Bernoulli
numbers (PL), and satisfy the identities: En(x + 1) + E
n(x) = 2xn.
Euler's conjecture. For g(k), in the Waring Problem (PL), Eulder conjectured that g(k) - 2k + [(3/2)k], where the bracketed term is the floor
function (PL).
Euler's formula. PL Euler's polyhedral
formula..
Euler's graph (network) formula. V + F - E = 1, where V denotes number of graphic
vertices, F denotes number of graphic faces, E denotes number of graphic edges. In the case of a square with one diagonal,
for example, V = 4, F = 2, E
= 5, whence, V + F - E = 4 + 2 - 5 = 1. (PL Euler's polyhedral
formula).
Euler's polygon division problem.
finding how many ways a plane convex (PL) polygon (PL) of n
sides can be divided into triangles by diagonals. Euler first proposed this problem to
Christian Goldbach in 1751. The solution is the Catalan number (PL).
Euler's polyhedral formula (topological characteristic)
. V + F - E = 2, where V
denotes number of polyhedral vertices, F denotes
number of polyhedral faces, E denotes number of polyhedral
edges. In the cube, for example, V = 8, F = 6
, E = 12, whence, V + F - E = 8 + 6 - 12 = 2
. (PL Euler's graph formula and PL Gibb's phase rule, for homology.)
Euler's rotation theorem. Any
rotation may be encapsulated in terms of exactly three angles (PL Euler angles
.)
even function. A function, f(x) s. t. f(x)= f(-x). (PL odd function.)
even number. A number (evenly) divisible
by two..
event. A measurable
subset of a probability space. In Statistics, a subset of the sample space
of all possible outcomes of an experiment.
evolute. The locus (PL) of
centers of curvature (the envelope, PL) of the normals 9PL) of a plane curve
.
exact differential. The differential
, df = p(x,y)dx + q(x,y)dy is exact if
n=0En
tn/n!. The Euler polynomials are related to the Bernoulli
numbers (PL), and satisfy the identities: En(x + 1) + E
n(x) = 2xn.
Euler's conjecture. For g(k), in the Waring Problem (PL), Eulder conjectured that g(k) - 2k + [(3/2)k], where the bracketed term is the floor
function (PL).
Euler's formula. PL Euler's polyhedral
formula..
Euler's graph (network) formula. V + F - E = 1, where V denotes number of graphic
vertices, F denotes number of graphic faces, E denotes number of graphic edges. In the case of a square with one diagonal,
for example, V = 4, F = 2, E
= 5, whence, V + F - E = 4 + 2 - 5 = 1. (PL Euler's polyhedral
formula).
Euler's polygon division problem.
finding how many ways a plane convex (PL) polygon (PL) of n
sides can be divided into triangles by diagonals. Euler first proposed this problem to
Christian Goldbach in 1751. The solution is the Catalan number (PL).
Euler's polyhedral formula (topological characteristic)
. V + F - E = 2, where V
denotes number of polyhedral vertices, F denotes
number of polyhedral faces, E denotes number of polyhedral
edges. In the cube, for example, V = 8, F = 6
, E = 12, whence, V + F - E = 8 + 6 - 12 = 2
. (PL Euler's graph formula and PL Gibb's phase rule, for homology.)
Euler's rotation theorem. Any
rotation may be encapsulated in terms of exactly three angles (PL Euler angles
.)
even function. A function, f(x) s. t. f(x)= f(-x). (PL odd function.)
even number. A number (evenly) divisible
by two..
event. A measurable
subset of a probability space. In Statistics, a subset of the sample space
of all possible outcomes of an experiment.
evolute. The locus (PL) of
centers of curvature (the envelope, PL) of the normals 9PL) of a plane curve
.
exact differential. The differential
, df = p(x,y)dx + q(x,y)dy is exact if
 df is path-independent, requring that
df = Dxf dx + Dyf dy.
exact first-order ordinary differential equation
. The equation, p(x, y)dx + q(x, y)dy = 0, is exact if
Dyp = Dxq. Then a conservative field exists
such that a potential function can be defined..
exceptional Jordan algebra. A Jordan
algebra (PL) which is not isomorhic to a subalgebra.
excluded middle. A method of proof
(PL), also labeled "tertium non datur" and "proof by contradiction". When a thesis cannot
be proven directly or constructivvely (PL), its contradiction is assumed, the
consequences of this are logically developed, and -- if another contradiction results -- it is
claimed that the original thesis has been proven, as if "truth-and-falsity" were a simple
dipole switch. The label "excluded middle" implicilty claims that only true and false
statements are acknowledged, so that "the middle" of "unproven" is excluded.
exclusive OR. Given logical
statements, P, Q, their standard ("inclusive") OR, P OR Q means "either one statement is the case, or the other, or both". The
exclusive OR means "either one statement, or the other, but not both".
existential quantifier. An operator
(PL) in predicate logic (calculus) (PL), denoted
df is path-independent, requring that
df = Dxf dx + Dyf dy.
exact first-order ordinary differential equation
. The equation, p(x, y)dx + q(x, y)dy = 0, is exact if
Dyp = Dxq. Then a conservative field exists
such that a potential function can be defined..
exceptional Jordan algebra. A Jordan
algebra (PL) which is not isomorhic to a subalgebra.
excluded middle. A method of proof
(PL), also labeled "tertium non datur" and "proof by contradiction". When a thesis cannot
be proven directly or constructivvely (PL), its contradiction is assumed, the
consequences of this are logically developed, and -- if another contradiction results -- it is
claimed that the original thesis has been proven, as if "truth-and-falsity" were a simple
dipole switch. The label "excluded middle" implicilty claims that only true and false
statements are acknowledged, so that "the middle" of "unproven" is excluded.
exclusive OR. Given logical
statements, P, Q, their standard ("inclusive") OR, P OR Q means "either one statement is the case, or the other, or both". The
exclusive OR means "either one statement, or the other, but not both".
existential quantifier. An operator
(PL) in predicate logic (calculus) (PL), denoted 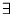 , meaning
"for at least one _". PL universal quantifier.
expansion. Label applied to power of
a polynomial. For example, in (x + y)2 = x2 + 2xy + y
2, the right-hand side is the expansion of the left-hand side.
exponent. The symbolic superscript used
in writing an exponentiation (PL). For example, in 102 = 100
, the superscript "2" is exponent. PL base, power, logarithn.
exponential. Applied to
exponentiation (PL). PL also exponential number and exponential function.
exponential curve. Graph of equation
using exponential function (PL), as in y = e. Isaac
Newton (1643-1727) used y = e- xin his "law of cooling of
liquids", typical of its applications since then. The compound interest function (PL)
approaches y = ex "in the limit", hence, is used in
approximating compound interest for large initial values.
exponential density function. The
density function (PL) of the statistical exponential distribution (PL).
exponential distribution. The
statistical distribution given by the density function, f(x) =
ae-ax, x > 0; f(x) = 0, x = 0. Remarkably, this
function's mean (PL) and variance (PL) are equal. (PL fidance.)
exponential equation. Given by y = ex or y = e- x
exponential function. The function,
ex = 1 + x + x2/2! + x3/3! + ... + xn
/n! + ...., where factorial (PL), n!
, meaning
"for at least one _". PL universal quantifier.
expansion. Label applied to power of
a polynomial. For example, in (x + y)2 = x2 + 2xy + y
2, the right-hand side is the expansion of the left-hand side.
exponent. The symbolic superscript used
in writing an exponentiation (PL). For example, in 102 = 100
, the superscript "2" is exponent. PL base, power, logarithn.
exponential. Applied to
exponentiation (PL). PL also exponential number and exponential function.
exponential curve. Graph of equation
using exponential function (PL), as in y = e. Isaac
Newton (1643-1727) used y = e- xin his "law of cooling of
liquids", typical of its applications since then. The compound interest function (PL)
approaches y = ex "in the limit", hence, is used in
approximating compound interest for large initial values.
exponential density function. The
density function (PL) of the statistical exponential distribution (PL).
exponential distribution. The
statistical distribution given by the density function, f(x) =
ae-ax, x > 0; f(x) = 0, x = 0. Remarkably, this
function's mean (PL) and variance (PL) are equal. (PL fidance.)
exponential equation. Given by y = ex or y = e- x
exponential function. The function,
ex = 1 + x + x2/2! + x3/3! + ... + xn
/n! + ...., where factorial (PL), n!  n(n - 1)(n- 2)(n - 3)...(2)(1). It arises from the equation y =
ln x, for natural logaritm, "ln" (PL). Remarkably, the exonential function
equals its derivative, that is, Dxex = ex
. It "passes to the limit" so nicely that it is used as a comparator in testing
convergence (PL) of other series (PL). A base (PL) for exponentiation
(PL) can be used other than e, but easily related to it. Thus, bx = ex ln b.
exponential number. The irrational
number, e = 2.718281..., given by the exponential series
(PL). PL also exponent and exponential function.
exponential series. The series
(PL), e = 1/0! + 1/1! + 1/2! ? 1?3! + ... + 1/n! + ..., where
factorial (PL), n!
n(n - 1)(n- 2)(n - 3)...(2)(1). It arises from the equation y =
ln x, for natural logaritm, "ln" (PL). Remarkably, the exonential function
equals its derivative, that is, Dxex = ex
. It "passes to the limit" so nicely that it is used as a comparator in testing
convergence (PL) of other series (PL). A base (PL) for exponentiation
(PL) can be used other than e, but easily related to it. Thus, bx = ex ln b.
exponential number. The irrational
number, e = 2.718281..., given by the exponential series
(PL). PL also exponent and exponential function.
exponential series. The series
(PL), e = 1/0! + 1/1! + 1/2! ? 1?3! + ... + 1/n! + ..., where
factorial (PL), n!  n(n - 1)(n- 2)(n - 3)...(2)(1)
, and 0! = 1!
n(n - 1)(n- 2)(n - 3)...(2)(1)
, and 0! = 1!  1.
exponentiation. This arithmetical
operation arises from the tedium of repeated multiplication. It is defined recursively:
b0 = 1, b(p + 1) = bp * b, p = 1, 2, .....
Exponentiation is well-defined (both left- and right-) (PL), hence, has two inverses (PL).
Whereas well-defined addition, multiplication are commutative (PL), merging their two
inverses into one, exponentiation is noncommutative -- thus, 23
= 8, 32 = 9 -- hence, exponentiation has two distinct inverses. Given bp = x, its b-inverse is logbx = p;
its p-inverse is root extraction, (x)1/p = b. Both are
partial in naturals, integers, rationals. The real numbers arise to render total
logarithm; complex numbers, to render total root extraction. (PL these systems.)
expression (algebraic). Constructed from
functands (PL), {x1, x2, ..., xn}
and numerical coefficients (PL) by arthmetic operations.
exsecant. Secant minus one.
extensionality (of sets). Two sets are
extensionally equivalent iff they contain the same members (ignoring ordering). PL
equipotent, equipollence, extollence.
extension field. A field (PL),
H, is an extension field, H/F, of field,
F, if the latter is a subfield of the former. Thus, the complex
field is an extension field of the real number field, in turn an extension
field of the rational number field.
extension ring. A ring (PL),
S, is an extension ring, S/R, of ring,
R, if the latter is a subfield of the former. Thus, both, Q, the rational number field, and Z[I], the
ring of Gaussian integers, are extension rings of Z, the
ring of integers.
exterior algebra. The algebra of the
exterior product (a.k.a. alternating algebra (PL) and Grassmann algebra). It
requires an exotic operation, pullback (PL), to link with the interior algebra of the
interior product. But multivector theory (PL) (a.k.a. geometric algebra,
Clifford algebra) includes both of these algebras within it and includes both of these
products in its multiproduct (PL) (a.k.a. geometric product, Clifford product
), which is absent from both interior and exterior algebras.
exterior angle. The angle formed by the
side of a polygon and the extension of an adjacent side.
exterior derivative. For a function,
f, it is the one-form, df =
SiDxif dxi, written in a coordinate
chart (PL), (x1, x2, ..., xn).
Taking function as a 0-form, the exterior derivative extends linearly to all
differential k-forms via the formula, d(a +
b) = da
1.
exponentiation. This arithmetical
operation arises from the tedium of repeated multiplication. It is defined recursively:
b0 = 1, b(p + 1) = bp * b, p = 1, 2, .....
Exponentiation is well-defined (both left- and right-) (PL), hence, has two inverses (PL).
Whereas well-defined addition, multiplication are commutative (PL), merging their two
inverses into one, exponentiation is noncommutative -- thus, 23
= 8, 32 = 9 -- hence, exponentiation has two distinct inverses. Given bp = x, its b-inverse is logbx = p;
its p-inverse is root extraction, (x)1/p = b. Both are
partial in naturals, integers, rationals. The real numbers arise to render total
logarithm; complex numbers, to render total root extraction. (PL these systems.)
expression (algebraic). Constructed from
functands (PL), {x1, x2, ..., xn}
and numerical coefficients (PL) by arthmetic operations.
exsecant. Secant minus one.
extensionality (of sets). Two sets are
extensionally equivalent iff they contain the same members (ignoring ordering). PL
equipotent, equipollence, extollence.
extension field. A field (PL),
H, is an extension field, H/F, of field,
F, if the latter is a subfield of the former. Thus, the complex
field is an extension field of the real number field, in turn an extension
field of the rational number field.
extension ring. A ring (PL),
S, is an extension ring, S/R, of ring,
R, if the latter is a subfield of the former. Thus, both, Q, the rational number field, and Z[I], the
ring of Gaussian integers, are extension rings of Z, the
ring of integers.
exterior algebra. The algebra of the
exterior product (a.k.a. alternating algebra (PL) and Grassmann algebra). It
requires an exotic operation, pullback (PL), to link with the interior algebra of the
interior product. But multivector theory (PL) (a.k.a. geometric algebra,
Clifford algebra) includes both of these algebras within it and includes both of these
products in its multiproduct (PL) (a.k.a. geometric product, Clifford product
), which is absent from both interior and exterior algebras.
exterior angle. The angle formed by the
side of a polygon and the extension of an adjacent side.
exterior derivative. For a function,
f, it is the one-form, df =
SiDxif dxi, written in a coordinate
chart (PL), (x1, x2, ..., xn).
Taking function as a 0-form, the exterior derivative extends linearly to all
differential k-forms via the formula, d(a +
b) = da  b + (-1)p a
b + (-1)p a  db
, where a is a k-form and
db
, where a is a k-form and
 is the wedge product. The exterior derivative is a (k + 1)-
form. Thus, for a k-form, w1 =
b1 dx 1 + b2 dx3, the exterior derivative is
dw1 = db1
is the wedge product. The exterior derivative is a (k + 1)-
form. Thus, for a k-form, w1 =
b1 dx 1 + b2 dx3, the exterior derivative is
dw1 = db1  dx1 + db2
dx1 + db2  dx2.
extollence, extollent sets. Sets are
extollent ("extollently equivalent") iff they have the same members to the same
tokenage (PL o-sets and multisets.)
extreme-value theorem (Weierstras e. v. t.).
A function which is continuous on a closed interval, [a, b]
has both a maximum and a minimum on this interval. An extreme value
on the open interval, (a, b), occurs at a critical point.
extremum. A maximum or minimum
, which may be local or global.
dx2.
extollence, extollent sets. Sets are
extollent ("extollently equivalent") iff they have the same members to the same
tokenage (PL o-sets and multisets.)
extreme-value theorem (Weierstras e. v. t.).
A function which is continuous on a closed interval, [a, b]
has both a maximum and a minimum on this interval. An extreme value
on the open interval, (a, b), occurs at a critical point.
extremum. A maximum or minimum
, which may be local or global.
 7 = 3 + REMAINDER 3. So 1/4 = 6/24 is the ANSWER.
7 = 3 + REMAINDER 3. So 1/4 = 6/24 is the ANSWER.
 2 = 17 + REMAINDER 1. So 1/18 is the ANSWER.
2 = 17 + REMAINDER 1. So 1/18 is the ANSWER.
 (t, x, y, z), t > 0).
(t, x, y, z), t > 0). , -b2 < h <
-c2, -a2 < z < -b2.
, -b2 < h <
-c2, -a2 < z < -b2.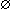 . Also, labeled null set.
. Also, labeled null set. j
j  S
S df is path-independent, requring that
df = Dxf dx + Dyf dy.
df is path-independent, requring that
df = Dxf dx + Dyf dy.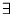 , meaning
"for at least one _". PL universal quantifier.
, meaning
"for at least one _". PL universal quantifier. b + (-1)p a
b + (-1)p a