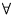a, b e R 
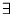x e M s. t. ax 
bx.
a b
n, (a,b) = 1, arranged increasingly.Thus: F1 = {0/1, 1/1}, F2 = {0/1, 1/2, 1/1}, F3= {0/1, 1/3, 1/2,
2/3, 1/1}, F4 = {0/1, 1/4, 1/3, 1/2, 2/3, 3/4, 1/1}, etc.
lim
inf fn dm lim inf fn
dm.
a (mod p). If p
does not divide a, there is a smallest exponent, d, s. t. ad - 1 0 (mod p)
and d divides a, hence, ap - 1 - 1 0(mod p). Y, is a preimage (imitator of
image) of an element y e Y. That is, f-1(y) = {x e X: f(x) = y}. Thus, foR
complex numbers, X, Y, f(z) = z2, every fiber
consists of two points, (z,-z), except for the fiber over zero,
which as one point (i.e., the fiber may be the empty set (PL)). Sometimes, the
fiber may be independent of choosing y e Y
Thus, if the fiber is a covering map (PL), then all fibers are discrete with same cardinality
. The above case, f(z) = z2 apart from zero, i.e. f(z) = z2 from the punctured complex plane, C - {0} to itself is a fiber consisting of two points
. When f:E M is a
fiber bundle, then every fiber is isomorphic in any appropriate category. Thus, for a
real fiber bundle of rank k, every fiber is isomorphic to
Rk. M, for total space (PL), L, and
base space (PL), M. Main condition for "fiberness": every point
of base space has a neighbhood (PL), N, which is homeomorphic
(PL) to N x F (set of all pairs (n, f)
, first component from neighborhood, second from fiber space) s. t. (locally) the
initiator of it all, L, resembles M x F
(set of all pairs, (m, f), with first component not
merely from the base space neighborhood but from all the base space, second from fibers), except
that the fiber may be "twisted" (as in möboid, PL). A f.b. is associated with a
group action (PL) representing the different ways the fiber can be viewed as equivalent., on a set C
in which either x y or y
x for every x, y in C. Given
a nonempty element of a poset (PL), a filter is set of all elements of chains
"ascending from" this element. A subfilter is a substructure of a filter satisfying
filter conditions. (PL ultrafilter.) The inverse structure is an ideal
(PL). fr+1 - fr, with D
frk, as the kth forward
difference; the backward difference: 
fr
fr - fr-1, with frk, as the kth
backward difference. This leads to finite difference equations (PL), homologues of
differential equations (PL).y; if
F(x, gy) = |g|F(x, y), for any
element (x, y) of T(M) and any
real number g; also, if metric
gij = ½(Dyiyj
|F(x, y)}|2) is a positive definite matrix. A differentiable manfold
with a Finsler metric is a Finsler space.
a, b g(b), g(a) - a 0,
0 g(b) - b. The continuity invokes the intermediate value
theorem that there exists a c e [a, b]
s. t. g(c) = c, hence, a fixed point in [a, b]
. The literature credits many fixed-point theorem to various mathematicians.
Perhaps the one most frequently applied and appearing in the literature is the Brouwer
fixed-point theorem. AC; choose natural number r for G = Cr; set B = C-1A-1C;
publish A, B, G, n, keeping C for encryption
. Encription procedure: represent message as 2 x 2 matrix
m with entries in Z
n; randomly choose natural number for E = G-1
AG2, K = G-1BG2; encript message as KmK; transmit (Km
K, E). Decryption: set L = C-1EC so that m = LKmKL; since G, C commute, we have: LKm
KL = (C-1EC)KmK(C-1EC) = (C-1G-s
AGsC)(G-sC-1ACGs)m
(C-1G-sAGsC)(G-sC-1ACGs) =
m, the original message.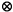
R, is an
exact functor (PL). Rn, placing each nonempty component of
Fa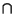 
U onto a parallel translation of the
standard hyperplane, Rn-c
in Rn. Each
Fa is a leaf and is not necessarily closed or compact.
s L along the length, L, of the knot, the
frame, Kj, associated with the knot is
ym = xm(s) + enm(s), where e
is a small parameter and nm(s) is a
unit vector field normal to the curve at s. V is a compact operator
(such as an interval operator with smooth kernel): any nonzero l which is not an eigenvalue of a compact operator is part of
the resolvent, i.e., (T - lI)-1
, is bounded, especially for finite-dimensional V,
so that any nondegenerate matrix is diagonal (PL).
abK(x, t)y(t)dt; of second kind: y(x) = f(x) + la
bK(x, t)y(t)dt, for which f(x), K(x,t) are known
functions, but y(x) is to be found, and K(x,t)
is the kernel of the integral equation.
æDsTö æ 0 k 0ö æTö
çDsN÷ = ç-k 0 t÷ çN÷
èDsBø è 0 -t 0ø èBø
where T is the unit tangent vector, N is
the unit normal vector, B is the unit binormal vector,
k is the curvature, and t is the
torsion. S
i n fi.
l0. (PL Perron-Frobenius theorem.- the occupancy/nonoccupancy of set elements in set theory or probability theory;
- truth/falsity of statements of a statement logic;
- the partial ordering in a lattice (perhaps only so used here).