 , on a set C
in which either x
, on a set C
in which either x  y or y
y or y
 x for every x, y in C. Given
an element of a poset (PL), an ideal is set of all elements chained to this
element. The inverse structure is an filterA simpler defintion readily derives
via the concept of CHAIN: Nonempty linearly ordered set or partial ordering
x for every x, y in C. Given
an element of a poset (PL), an ideal is set of all elements chained to this
element. The inverse structure is an filterA simpler defintion readily derives
via the concept of CHAIN: Nonempty linearly ordered set or partial ordering  , on a set C
in which either x
, on a set C
in which either x  y or y
y or y
 x for every x, y in C. Given
a nonempty element of a poset (PL), a filter is set of all elements in chains "rising
to" this element. A subideal is a substructure of an ideal satisfying the
conditions for an ideal. (PL ultra-ideal.) The inverse structure is a
a filter (PL). (PL).
x for every x, y in C. Given
a nonempty element of a poset (PL), a filter is set of all elements in chains "rising
to" this element. A subideal is a substructure of an ideal satisfying the
conditions for an ideal. (PL ultra-ideal.) The inverse structure is a
a filter (PL). (PL).- S+x,y = S(x + y) = x2 + y2 + 2xy, as before.
- +Sx,y = +x2, y2 = x2 + y2.
 V
V 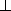 W . Generally, V · W = Sm
i=1xiyi = x1y1 + ... + xnyn
. This product is invariant under a rotation: (using Einstein summation,
PL) V' · W' = ViWi = cijUj
cikVk = (cijcik)UjVk =
dUjVk = UjVj = V · W
. (For tensors (PL): S · T = Sa
Ta.) But an invariant (PL) is a
scalar, as we can verify in another way. U'xW'x
+ U'yW'y + U'zW'z = S
icxiUiSjcxjW
j + SicyiUiS
jcyjWj + Siczi
UiSjczjWj. Using indices,
k, l to run over x, y. z, we have: SkU'kW'k = Sl
SjSjcliUl
cljWj. Rearranging the right-side terms:
SkU'kW'k = S
lSjSi(c
liclj)UlWj = SiSjdijUiWj
= SiUiWi, that is, SkU'kW'k = S
iUiWi -- scalar. This can be written in terms of
another scalar, length: U · W = (U, W) = ||U - W|| .
Since, as shown below, this product is bilinear, squaring the previous result yields:
||U - W||2 = (U, U) - (U, W) - (W, U) + (W, W). But -- since
(U, U) = ||U||2, (W, W) = ||W||2, (U, W) = (W, U),
the previous result rearranges as: 2(U, W) = ||U||2 + ||W||2
- ||U - W||, which, by halving, becomes: (U, W) = ½
(||U||2+ ||W||2 - ||U - W||), the law of cosines. Inner
product is commutative or symmetric: V · W = W · V;
bilinear (U + W, Z) = (U, Z) + (V, Z), (U, W + Z) = (U, W) + (U, Z)
; positive definite: (U, U)
W . Generally, V · W = Sm
i=1xiyi = x1y1 + ... + xnyn
. This product is invariant under a rotation: (using Einstein summation,
PL) V' · W' = ViWi = cijUj
cikVk = (cijcik)UjVk =
dUjVk = UjVj = V · W
. (For tensors (PL): S · T = Sa
Ta.) But an invariant (PL) is a
scalar, as we can verify in another way. U'xW'x
+ U'yW'y + U'zW'z = S
icxiUiSjcxjW
j + SicyiUiS
jcyjWj + Siczi
UiSjczjWj. Using indices,
k, l to run over x, y. z, we have: SkU'kW'k = Sl
SjSjcliUl
cljWj. Rearranging the right-side terms:
SkU'kW'k = S
lSjSi(c
liclj)UlWj = SiSjdijUiWj
= SiUiWi, that is, SkU'kW'k = S
iUiWi -- scalar. This can be written in terms of
another scalar, length: U · W = (U, W) = ||U - W|| .
Since, as shown below, this product is bilinear, squaring the previous result yields:
||U - W||2 = (U, U) - (U, W) - (W, U) + (W, W). But -- since
(U, U) = ||U||2, (W, W) = ||W||2, (U, W) = (W, U),
the previous result rearranges as: 2(U, W) = ||U||2 + ||W||2
- ||U - W||, which, by halving, becomes: (U, W) = ½
(||U||2+ ||W||2 - ||U - W||), the law of cosines. Inner
product is commutative or symmetric: V · W = W · V;
bilinear (U + W, Z) = (U, Z) + (V, Z), (U, W + Z) = (U, W) + (U, Z)
; positive definite: (U, U)  0, (U,U) = 0
0, (U,U) = 0
 U = 0; associative: (rV) · W = r(V
· W); distributive: V · (W + Z) = (V · W) +
(W · Z). The derivative (PL) of the inner product of vectors is:
Dt(q(t) · r(t)) = q(t) · D1r(t) + Dt
q(t) · r(t) PL directional derivative. (A particular form of this
inner or dot or scalar product, via unit vectors, PL, and direction cosines, PL, and the
directional derivative, PL, results in the gradient, PL, which can be treated as an operator, PL,
to create a potential function, PL.)
U = 0; associative: (rV) · W = r(V
· W); distributive: V · (W + Z) = (V · W) +
(W · Z). The derivative (PL) of the inner product of vectors is:
Dt(q(t) · r(t)) = q(t) · D1r(t) + Dt
q(t) · r(t) PL directional derivative. (A particular form of this
inner or dot or scalar product, via unit vectors, PL, and direction cosines, PL, and the
directional derivative, PL, results in the gradient, PL, which can be treated as an operator, PL,
to create a potential function, PL.)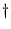 "
denoting complex conjugate): (u + v, w) = (u, w) + (v, w); (u, v + w) =
(u, v) + (u, w); (au, v) = a(v, w); (u, v)
"
denoting complex conjugate): (u + v, w) = (u, w) + (v, w); (u, v + w) =
(u, v) + (u, w); (au, v) = a(v, w); (u, v)
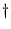 = (v, u); (u, u)
= (v, u); (u, u)  0, (u, u) = 0
0, (u, u) = 0  u = 0.
u = 0.  +n; [0,n]
+n; [0,n]  -n; [n, n] = [0, 0]
-n; [n, n] = [0, 0]  0
. (This is explained in a bypass.) PL
frinteger.
0
. (This is explained in a bypass.) PL
frinteger. xdx =
xdx =
 ydy =
ydy =
 udu =
udu =
 vdv =
vdv =
 wdw, etc.
wdw, etc."How could all of these indefinite integrals be equal?" Answer: each integrand is simply a placeholder for "the identity function" (in Menger's language), so it is homologous to saying, for example, 1 = 2 - 1 = 3 - 2 = 4 - 3 = 1 - 0, etc.
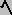 f,
v) = (u, v
f,
v) = (u, v  f). Combined with orthonormal basis (PL) units,
{ei}, we have orthogonality: e
1
f). Combined with orthonormal basis (PL) units,
{ei}, we have orthogonality: e
1 e2
e2 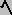 e3 = 0
; and "annihilation": e1
e3 = 0
; and "annihilation": e1 e2e
3
e2e
3 e4
e4 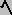 e1
e1 e4 = e2
e4 = e2 e3.
e3.- an left inverse iff it is left welldefined ("cancellative") for operands a,b,c: c o a = b o a implies that c = b;
- has a right inverse iff it is right welldefined ("cancellative"): a o b = a o c implies that b = c;
- has inverse iff it is has both a left and right inverse and is commutative (as with arithmetic addition, otherwise it has two inverses (as does arithmetic exponentiation).
 f,
v) = (u, v
f,
v) = (u, v  f). Combined with orthonormal basis (PL) units,
{ei}, we have orthogonality: e
1
f). Combined with orthonormal basis (PL) units,
{ei}, we have orthogonality: e
1 e2
e2 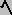 e3 = 0
; and "annihilation": e1
e3 = 0
; and "annihilation": e1 e2e
3
e2e
3 e4
e4  e1
e1 e4 = e2
e4 = e2 e3.
e3.- an left inverse iff it is left welldefined ("cancellative") for operands a,b,c: c o a = b o a implies that c = b;
- has a right inverse iff it is right welldefined ("cancellative"): a o b = a o c implies that b = c;
- has inverse iff it is has both a left and right inverse and is commutative (as with arithmetic addition, otherwise it has two inverses (as does arithmetic exponentiation).