O
_________________________________________________________________________________________________
- obelisk
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- object
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- object function
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- oblate spheroid
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- oblique
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- oblique angle
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- oblique coordinates
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- oblique coordinate system
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- oblique lines
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- oblique section
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- oblique triangle
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- obtuse
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- obtuse angle
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- obtuse triangle
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- octagon
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- octahedron
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- octal number system
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- octant
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- octillion
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- occupancy theory
. - A susbsystem of
combinatorics (a.k.a. combinatorial algebra, PL). In this theory, elements
(distinguishable or indistinguishable) are assigned by rule to cells (distingishable by ordering),
with or without restrictions on occupancy. PL boltzmannians, fermions, bosons, multons.
- odd function
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- odd number
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- o-intersection
. - Extenstion of the
set-theoretic operation of intersection (t-intersection, PL) to recognize multiple
tokens of type (Pl typon). Thus, given o-sets -- o-{a, a, a, b, c}
and o-{a, a, b, b, c, c}, their o-intersection is:
o-{a, a, a, b, c} 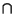 o o-{a, a, b, b, c, c}
~o o-{a, a, b, c} -- elements of same cardinality common to both sets.
o o-{a, a, b, b, c, c}
~o o-{a, a, b, c} -- elements of same cardinality common to both sets.
- o-join
. - Lattice homologue of
o-union(PL), as with homologues of o-sets given there: 120
 900 ~o 12000. Note that it is equivalent to LCM
(least common factor).
900 ~o 12000. Note that it is equivalent to LCM
(least common factor).
- o-math(ematics)
. - Mathematics which
recognizes both kind or type and also degree or order. The protypes are
factor theory and distributive lattice theory (PL). But it can be extended to set theory, statement logic, combination theory,
indicator theory, diagram theory. (Until this extension takes hold, we survive the
agstymie (PL) only to be stymied by the
tostymie.)
- o-meet
. - Lattice homologue of
o-intersection (PL), as with homologues of o-sets given there: 120
 900 ~o 60. Note that it is equivalent to GCF (greatest
common factor), which t-meet (PL) is not, being (herein) 30.
900 ~o 60. Note that it is equivalent to GCF (greatest
common factor), which t-meet (PL) is not, being (herein) 30.
- one-parameter group
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- one-parameter subgroup
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- one-point compactification
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- one's complement
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- one-sided limit
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- one-to-one
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- one-to-one function or one-to-one mapping
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- onto
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- open ball
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- open interval
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- open map
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- open mapping theorem
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- open set
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- operand
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- operation
. - A function
(PL) such that the codomain (output set) is a subset of the domain
(input set). An operation has an inverse (PL) iff it is a
one-one function. The positive case is well-defined
(cancellative), as exemplified by numerical addition. The
negative case is nonwell-defined (nonconcellative), as
exemplified by least common multiple (LCM) or greatest
common divisor (GCD). (PL these terms.)
-
- operational calculu
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- operations research
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- operator
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- operator theory
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
- optimal number system
. - This would be a
more enlightening label for the real number system (PL), since these are no more "real"
than any other numbers, rather all are merely linguistic. But these numbers are optimal
for specific conditions. Thus, the circle (with circumference, C, and diameter, d) is the plane figure providing
maximum area with minimum perimeter (optimality), encapsulated in the irrational
real number, p = C/d. Again, the square
is the polygon providing maximum area with minimum perimeter, and its
diagonal (segment equally subdividing figure, homologous to diameter of circle) is a
multiple of the square root of two, historically the first irrational real number
to be discovered. Another such irrational real is the golden mean (PL), praised in
many female forms, observed in Nature, and applied in architecture, sculpture, painting, etc.
Both Eudoxus (c. 408-355 BC) and Richard Dedekind (1831-1916) showed that a "slot" exists between
any consecutive pair of fractions. Students should be taught that the optimal number system
reveals to them some of the "secrets" of "Nature" -- "slots" to "squeeze in" any "just right"
beauty or utility -- motivating students to seek optimality in their individual and
public lives. (PL Bellman on this Homepage.)
- optimal policy
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- optimal system
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- optimization
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- optimization theory
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- OR
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orbit
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- order
. - A procedure for assigning
element to a sequence (PL). For example:
- The order of a derivative or differential operator refers to how many times it is applied.
- An n square matrix is said to be of order n.
- A polynomial with n as largest exponent of a term is of order (or degree)
n.
Etc. (PL order relation.) .
- ordered field
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- ordered pair
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- ordered ring
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- ordering
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- order of a differential equation
.
- May be read at http://www.harcourt.com/dictionary /browse/19/
.
- order of a graph
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- order of a group
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- order of an element
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- order of an elliptic function
.
- May be read at http://www.harcourt.com/dictionary /browse/19/
.
- order of a pole
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- order of a tensor
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- order of a zero
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- order of magnitude
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- order-preserving
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- order relation
. - A binary relation which is transitive (PL). (PL
also total ordering and partial ordering.)
- ordinal (extollent, PL) equivalence
. -
Equivalence in o-mathematics, PL -- arithmetic factor theory, sets, lattices, etc. --
which recognizes multiple tokens of a type (PL typon). It may be denoted as ~o. (PL t-union, o-union, t-intersection, o-intersection, t-join,
o-join, t-meet, o-meet.)
- ordinal number
. - The ordinal number
c is the transitive set (PL) of all ordinals
preceding c. (PL cardinal number and the
paradox of counting.) Children can easily be taught ordinality
via a brownbag model.)
- ordon
. - A gnomon (PL) of the ordinal
segment of measurement scales (PL).
- outerproduct (multivector)
. - xxxxxx
(PL innerproduct and multiproduct.)
- ordinary differential equation
.
- May be read at http://www.harcourt.com/dictionary /browse/19/
.
- ordinary point
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- ordinate
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- Ore's theorem
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orientable manifold
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orientation
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- origin
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthocenter
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthogonal
. - In elementary geometry:
perpendicular. For two vectors: zero inner product, a condition which extends
to any inner product space whereby two subspaces are orthogonal iff every element of
one is orthogonal to every element of the other subspace. Similar definitions for any
symmetric or alternating bilinear form, any Hermitian form.
- orthogonal basis
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthogonal complement
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthogonal functions
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthogonal group
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
- orthogonality
. - PL oethogonal. The
equations for rotation of coordinate axes (PL), can be rewritten, by defining, x = x>/sub>1, y = x2, a11 = cos q, a
12 = sin q, a21 = - sin q, a
22 = cos q, to become: x'1
= a11x1 + a12x2, x'2 = a21
x1 + a22x2. The coefficient, aij can be interpreted as one or more direction cosines (PL):
the cosine of the angle between x'i and x'j, that is, a12 = cos(x'1, x
2) = sin q, a21 = cos(x'2, x1
) = cos (q + p/2) = - sin q. Given this new notation, we can rewrite the previous coordinate
transformation in summation form: S
j=2j=1aijxj, i = 1, 2, which easily extends to
any number of dimensions. Now, the sine, cosine functions satisfy orthogonality conditions
: 1/L
 L
-L cos(jpL) cos(kpL)dx = 1/L
L
-L cos(jpL) cos(kpL)dx = 1/L
 L-Lsin(j
pL) sin(kpL)dx = d
jk<, where djk is
the Kronecker symbol (PL), s. t. djk
= 1, j = k and djk = 0, j
L-Lsin(j
pL) sin(kpL)dx = d
jk<, where djk is
the Kronecker symbol (PL), s. t. djk
= 1, j = k and djk = 0, j  k. djk = 1, j = k.
The orthogonality of the sine, cosine functions is inherited by their "encodments": aijajk = djk. Hence,
orthogonality is in implicit in the rotation of coordinate axes equations (PL),
hence, also in the test for vectorhood (PL) and in the inner product for vectors (PL)
or in general inner product spaces (PL).
k. djk = 1, j = k.
The orthogonality of the sine, cosine functions is inherited by their "encodments": aijajk = djk. Hence,
orthogonality is in implicit in the rotation of coordinate axes equations (PL),
hence, also in the test for vectorhood (PL) and in the inner product for vectors (PL)
or in general inner product spaces (PL).
- orthogonalization
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthogonally equivalent matrices
.
- May be read at http://www.harcourt.com/dictionary /browse/19/
.
- orthogonal matrix
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthogonal polynomials
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthogonal projection
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthogonal system
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthogonal trajectory
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthogonal transformation
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthogonal vectors
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthographic projection
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthonormal basis
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthonormal coordinates
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthonormal functions
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthonormal vectors
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- orthoptic
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- oscillating function
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- oscillation of a function
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- osculating circle
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- osculating plane
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- o-union
. - Union of o-sets (PL),
recognizing multiple tokenage of types (PL typons). Thus, given two o-sets --
o-{a, a, b, c, c} and {a, b, b, c} -- their
o-union is: o-{a, a, b, c, c}
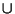 o {a, b, b, c}
~o o-{a, a, a, b, b, b, c, c, c}. Note that, for the factor homologues
of these o-sets -- respectively, 900, 90, 27000 -- it is their LCM (least common mulltiple),
while the t-union (PL) of these sets would be homologous only to 30.
o {a, b, b, c}
~o o-{a, a, a, b, b, b, c, c, c}. Note that, for the factor homologues
of these o-sets -- respectively, 900, 90, 27000 -- it is their LCM (least common mulltiple),
while the t-union (PL) of these sets would be homologous only to 30.
- outer automorphism
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- outerproduct (of multivectors, PL)
. Given
two multivectors of the same grade, their outerproduct raises this one grade. It is the
same as exterior product of differential forms theory. Thus, for basis vectors
, e1 = [1, 0] and e
2 = [0, 1], their outerproduct is: e1
Ùe2 = i =  -1. Then,
for vectors, a = [a1, a2], and b = [b1, b2], their outerproduct is a = (a1b2 - a2b1
) e1Ùe1 i = (a
1b2 - a2b1)
-1. Then,
for vectors, a = [a1, a2], and b = [b1, b2], their outerproduct is a = (a1b2 - a2b1
) e1Ùe1 i = (a
1b2 - a2b1)  -1, equivalent
to a multiple of the "imaginary vector", hence, a subplane of the plane containing the
component vectors. It is easily transformed into the standard cross or vector product of
vectors, projecting from the plane of the component vectors.
-1, equivalent
to a multiple of the "imaginary vector", hence, a subplane of the plane containing the
component vectors. It is easily transformed into the standard cross or vector product of
vectors, projecting from the plane of the component vectors.-
- oval
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
- oval of Cassini
. - May be
read at http://www.harcourt.com/dictionary /browse/19/
.
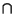 o o-{a, a, b, b, c, c}
~o o-{a, a, b, c} -- elements of same cardinality common to both sets.
o o-{a, a, b, b, c, c}
~o o-{a, a, b, c} -- elements of same cardinality common to both sets. 900 ~o 12000. Note that it is equivalent to LCM
(least common factor).
900 ~o 12000. Note that it is equivalent to LCM
(least common factor). 900 ~o 60. Note that it is equivalent to GCF (greatest
common factor), which t-meet (PL) is not, being (herein) 30.
900 ~o 60. Note that it is equivalent to GCF (greatest
common factor), which t-meet (PL) is not, being (herein) 30. L
-L cos(jpL) cos(kpL)dx = 1/L
L
-L cos(jpL) cos(kpL)dx = 1/L
 L-Lsin(j
pL) sin(kpL)dx = d
jk<, where djk is
the Kronecker symbol (PL), s. t. djk
= 1, j = k and djk = 0, j
L-Lsin(j
pL) sin(kpL)dx = d
jk<, where djk is
the Kronecker symbol (PL), s. t. djk
= 1, j = k and djk = 0, j  k. djk = 1, j = k.
The orthogonality of the sine, cosine functions is inherited by their "encodments": aijajk = djk. Hence,
orthogonality is in implicit in the rotation of coordinate axes equations (PL),
hence, also in the test for vectorhood (PL) and in the inner product for vectors (PL)
or in general inner product spaces (PL).
k. djk = 1, j = k.
The orthogonality of the sine, cosine functions is inherited by their "encodments": aijajk = djk. Hence,
orthogonality is in implicit in the rotation of coordinate axes equations (PL),
hence, also in the test for vectorhood (PL) and in the inner product for vectors (PL)
or in general inner product spaces (PL).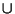 o {a, b, b, c}
~o o-{a, a, a, b, b, b, c, c, c}. Note that, for the factor homologues
of these o-sets -- respectively, 900, 90, 27000 -- it is their LCM (least common mulltiple),
while the t-union (PL) of these sets would be homologous only to 30.
o {a, b, b, c}
~o o-{a, a, a, b, b, b, c, c, c}. Note that, for the factor homologues
of these o-sets -- respectively, 900, 90, 27000 -- it is their LCM (least common mulltiple),
while the t-union (PL) of these sets would be homologous only to 30. -1. Then,
for vectors, a = [a1, a2], and b = [b1, b2], their outerproduct is a = (a1b2 - a2b1
) e1Ùe1 i = (a
1b2 - a2b1)
-1. Then,
for vectors, a = [a1, a2], and b = [b1, b2], their outerproduct is a = (a1b2 - a2b1
) e1Ùe1 i = (a
1b2 - a2b1)  -1, equivalent
to a multiple of the "imaginary vector", hence, a subplane of the plane containing the
component vectors. It is easily transformed into the standard cross or vector product of
vectors, projecting from the plane of the component vectors.
-1, equivalent
to a multiple of the "imaginary vector", hence, a subplane of the plane containing the
component vectors. It is easily transformed into the standard cross or vector product of
vectors, projecting from the plane of the component vectors.