[Apologies to Cow Cow Davenport]
		Hill Bert doan low no kunstrukty-vizm rown here.
		Hill Bert doan low no kunstrukty-vizm rown here.
		Ah doan keer whut Hill Bert doan low!
		Gonna kunstruk mah vizm anys how!
		Brrrp! Brrrp! Brrrp! Brrrp! Brrrp! [finger-on-lip music]

When mathematicians cannot find a constructive proof of a theorem, resort is made to a nonconsructive proof, such as reductio ad absurdum (a.k.a. proof-by-contradiction):

1. assume the contradiction of what is to be proven;
2. proceed until this yields another contradiction;
3. conclusion: this contradiction of a contradiction proves what is to be proven.

For example, here is Euclid's Proof of the Theorem: The square root of two is not a rational number. Given a square of one unit on each side: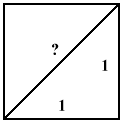What is the diagonal length? By the Pythagorean Theorem, we find: 1² + 1² = 2. Hence, the diagonal length is: 2. But what sort of number is this? Theorem says it isn't rational, that is, not a ratio of two "whole number".

To prove this, we first need to prove a Lemma: The square root of an even number is even; of an odd number, is odd. Proof: An even "whole number" has the form 2n, for number n. Then its square has the form 4n² = 2(2n²), the form of an even number. (An odd "whole number" has the form 2n + 1, for number n. Then its square has the form 4n² + 4n + 1 = 2(2n² + 2n) + 1, the form of an odd number.) Hence, the square root of a number is even if, and only if, the numer is even.

Reductio Proof of Theorem: The square root of two is not a rational number:

1. assume it is rational, as defined above, for "whole numbers" a,b , that is, 2 = a/b, where the fraction a/b cannot be reduced (!);
2. given this equality, we can square both of its sides to "get a whole number on the left": 2 = a²/b²;
3. we can simplify this by multiplying both sides by b², obtaining: 2b² = a²;
4. by our even definition, a² is even, and by our Lemma, we find that a is even, that is, of the form a = 2c, for some "whole number" c;
5. let's put that last result in (3): 2b² = 4c² , and we can simplify this by dividing both sides by 2: b ² = 2c²;
6. but that last result says b² is an even number, which (by Lemma) means that b is even;
7. hence, we now have arrived at a contradiction of our original assumption that a/b cannot be reduced, for, if both a,b are even, then such a fraction can be reduced;
8. hence, this contradiction of a contradiction is said to prove that the square root of two is not a rational number. QED.

Since the Greeks had no conception of an irrational number, this meant that:

• the diagonal of a square cannot be assigned a number;
• and this meant that, contrary to the position of The Pythagoreans, geometry and arithmetic are incompatable;
• and, since Plato's Academy preached that "motion is geometry set to time", this meant that motion cannot be arithmetized;
• and this explains the fact that the gravest charge against Galileo (x-y) was not saying that the earth revolves around the sun, but rather of being a "Pythagorean" in his arithmetical "law of falling bodies";
• finally, this inhibited development of theoretical mechanics for 2000 years, perpetuating slavery.

History was "hung up" by a nonconstructive proof! Worship of nonconstructive mathematics resulted in this.

Such thinking was challenged (in early 20th century) by a Dutch mathematician, L. E. J. Brouwer (1881-1966), who, among other contributions, accomplished important results in the burgeoning field of topology. Brouwer accepted nonconstructive proofs only in the FINITE, since (at least, theoretically) it could thereby be checked out.

Brouwer questioned: If a criminal, in committing a crime succeeds in destroying the only evidence that could convict him, must we declare him innocent? Brouwer said, "No!", demanding a third judgment, "Not proven". Scottish jurisprudence has just such a verdict, and it was discussed in the trial in Lockerbee, Scotland, about the people killed by a bomb on a plane. During the discusssions about impeaching President Clinton, Pennsylvania Senator Spector suggested this form of verdict. A 1950 film, "Madeleine", sometimes seen on TV, directed by the great director, David Lean, ends with a "Not Proven" verdict. (Based on a true 19th century story, Madeleine is accused of poisoning her faithless lover by arsenic in a cup of chocolate. The Crown can't prove she actually put the arsenic in the drink, but the jury does not consider her innocent, so brought in a verdict of "Not Proven", sending Madeleine away "under a cloud of suspicion".) Regarding nonconstructiveness in mathematics, I published a fable.

Lawyers for gangsters have regularly taken advantage of our bivalent justice by forcing trials of their clients before the presecution is ready. Then, when insufficient evidence is cited, the jury finds the "accused" innocent, since it cannot find him guilty; and then he cannot be tried again because of "double jeopardy". This (along with other quandaries of decision-making) has motivated some logicians to introduce several forms of multi-valued logic into the literature.

Implicitly, Brouwer did not accept Euclid's proof of the nonrationality of the square root of two.

When Hilbert, the "formalist", heard of Brouwer's "apostasy", Hilbert wrote, "To take the reductio proof away from the mathematician is like taking the telescope away from the astronomer or the microscope away from the biologist."

Hilbert was holding to the "bivalent" tradition going back to Chrisippus the Stoic (x-y) -- that a statement is either true or false, which led to the reductio argument having another name: "tertium non datur" -- "no third way".

I mention it to draw attention to "bivalency" about proofs. I hold that only constructive proofs constitute first class mathematics for a very good reason: history shows a constructive proof tells us much more than a nonconstructive one. But I also accept a nonconstructive proof as second class mathematics for another very good reason: history shows that existence of a nonconsructive proof often motivates discovery of a constructive proof of the same mathematical statement, advancing mathematics. I've advocated this position for over 30 years.

So? I've been denounced by adherents of both sides -- by constructivists and by nonconstructivists. I've been denounced outside meetings of The Mathematical Association of America. And I've received insulting letters. To adherents of both sides, I'm apparently a "heretic".

Is it any wonderful that mathematics appears to some as a kind of religion? The Holy Church of Platonism.