We need notation for the MULTIPRODUCT of 2 or more BASIS UNITS, say, I
n, n = 1, 2, .... (In our previous notation, I1
i = 
¯1 and I I2. We consider the TRIVECTOR, I3
d1 
d2d3.
REVERSION (the main anti-automorphism in MULTIVECTORS), applied to this TRIVECTOR,
reverses the ORDERING of its SUBSCRIPTS TO YIELD its CONJUGATE, I
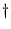. A transposition is
an interchange of two adjacent elements in an ordering. Each transposition in the
ordering of subscripts in this TRIVECTOR turns it into its NEGATIVE:
I = d1d
2d3
¯d2d
1d3 = +
d2
d3d1 = ¯d3
d2d1 = I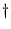. Thus, REVERSION of TRIVECTOR
I YIELDS ITS CONJUGATE, I
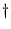, such that I
I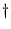 = 1. (The MULTIVECTOR
equivalent of i ( ¯i) = (¯1)(¯
¯1) = 1.)
To generalize this, we need another result. I've never seen this in Clifford Algebra, but it resembles a little known algorithm in permutation theory, and reversion is a permutational operation. In the theory of permutation groups (a.k.a. theory of the symmetric group, Sn, on n elements, ALL OPERATIONS CAN BE REDUCED TO EXACTLY TWO:
- TRANSPOSITION OF TWO ADJACENT ELEMENTS;
- DISPLACEMENT OF RIGHT-MOST ELEMENT IN ORDERING TO LEFT-MOST POSITION.
A single TRANSPOSITION in a MULTIPRODUCT (say, shift to left) MULTIPLIES THE MULTIPRODUCT by (¯1) -- just as ODD PERMUTATIONS are denoted NEGATIVELY, EVEN PERMUTATION denoted POSIIVELY. (The SET OF EVEN PERMUTATIONS is THE ALTERNATING GROUP, An, a PROPER SUBGROUP of Sn.)
Suppose that the conjugate of In, denoted In†, REQUIRES j such TRANSPOSITIONS, invoking a MULTIPLIER of (¯1)j, that is, In† = (¯1)jIn. [x1]
Now, the (n+1)-conjugate, In+1†, is simply THE LEFT PRODUCT of dn+1 with In†, namely, In† = dn+1In†.[x2]
Substitution of [x1] in [x2] yields In† = dn+1(¯1)jIn = (¯1)jdn+1In. [x3] This describes the FIRST MINIMAL OPERATION (involving TRANSPOSITIONS).
To deal with the SECOND MINIMAL OPERATION, suppose it takes k TRANSPOSITIONS to SHIFT dn+1, in In+1, from RIGHT-MOST POSITION to LEFT-MOST, invoking a (¯1)k MULTIPLIER. That is, dn+1In = (¯1)kIn.[x4]
Substitution of [x3] in [x4] yields: In+1† = (¯1)j(¯1)kIn+1 = (¯1)j+kIn+1. Going back from n+1 to n, we have:In† = (¯1)j+kIn+1.[x5]
Thus, [x5] tells us that j+k TRANPOSITIONS TRANSFORMS In into its CONJUGATE, In†, invoking the MULTIPLIER (¯1)j+k.
I'll illustrate for two known (previous) cases. We readily see that d1Äd2 = ¯(d2Äd1). ONE TRANSPOSITION to REVERT or CONJUGATE. We can use this result, with n = 2, for the case of n + 1 = 3.
Given the ordering 123, clearly, 2 TRANSPOSITION SEND this RIGHT-MOST 3 to LEFT-MOST POSITION: 123 → 312, so k = 2. And we found j = 1, for ORDERING 12. Hence, j + k = 1 + 3 = 3 TRANSPOSITIONS yield d2ÄI2 = (¯1)3I3. Hence, I3† = (¯1)3I3 = (¯1)I3, as we found earlier. Neither I2 is INVARIANT UNDER REVERSION. But let's consider n = 4.
From the previous case, setting j = 3, consider the ORDERING, 1234. Clearly, 3 TRANSPOSITIONS shift 4 to LEFT-MOST POSITION, 1234 -> 4123. Then, j + k = 3 + 3 = 6 TRANSPOSITIONS. That is, I4† = (¯1)6I4 = I4. Looky! I4 IS INVARIANT REVERSION -- is its OWN CONJUGATE!
Another involution (self-inversive permutation) is INVERSION: MULTIPLYING ALL VECTOR COMPONENTS by (¯1). Still another involution is REVERSION followed by INVERSION, or vice versa, which I label "coversion". It can be shown that I4 is INVARIANT under REVERSION, INVERSION, COVERSION! It is EQUIVALENT Dirac's MATRIX OPERATOR, g5, applied in relativistic quantum field theory.
Note also that all the familiar metrics can be obtained in Clifford Algebra by these three involutions.
ASSIGMENT: Find why these involutions serve this special purpose.
Hestenes has uniquely shown
projective geometry within multivector theory:
"I call the two most important intepretations [of Geometric Algebra] the metrical ["of the
quadratic form"] and the projective interpretations....The projective interpretation of
R3 is set by identifying the nonzero vectors in R3
with points in the projective plane P2. Two points a, b are "the same" if and only if a b = 0.
"The entire algebra R3 now serves to characterize the geometry of the projective plane. The join of two distinct points a, b determines a line A, and this can be expressed by the
equation A = a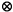 
b. (6)
"Thus, lines in projective geometry are represented by bivectors. Contrast this with the metrical interpretation of bivectors as 'directed areas' or 'plane segments'. These different interpretations are reflected in differences in the diagrams for the projective and metrical geometries, though our algebraic representation reveals a common underlying algebraic structure.
"As indicated by (6), the projective relation 'join' is represented by the outer product.
Thus, the join of three distinct points, or the join of a line and a point, is a plane, as
expressed by a 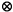b
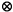c = A 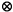c = P. (7)
"Another basic relation in projective geometry is the meet. The meet (or intersection) of lines A, B in a point p can be expressed by the equation A Ú B = p. (8)
"To see how this relates to the geometric product, we need the concept of duality. Remarkably,
duality in geometric algebra is homomorphic to duality in projective geometry. The
algebraic dual à of a vector a
in R3 is a bivector A determined by the equation
A = à º ai, (9)
where, as before, i is the unit pseudoscalar. Now the meet relation in (8) can be defined by writing A Ú B = à · B = (ia) · B. (10)
"Thus, the meet is a composite of duality and the inner product. Despite the appearance of the inner product in (10), the meet is a nonmetrical relation. The meet is independent of signature because the inner product is actually used twice in (ia) · B = (i · a) · B.
"With the projective interpretation just set forth, all the theorems of projective geometry can be formulated and proved in the language of geometric algebra. The theorems take the form of algebraic identities. These identities also have metrical interpretations and therefore potential applications to physics. Indeed, the common formulation in terms of R3 shows that metrical and projective geometries share a common algebraic structure, the main difference being that projective geometry (at least of the elementary type considered here), employs only the multiplicative structure of geometric algebra. Since both inner and outer products are needed for projective geometry, the geometric product which underlies them is necessary and su±cient as well."
Hestenes also explains about differential geometry within Geometric [Multivector]
Calculus:
"The development of Geometric Algebra into a full-blown Geometric Calculus capable of
handling all aspects of differential geometry requires a fusion of differential and integral
calculus with the concepts of geometric algebra. This task has been carried out in [elsewhere] with considerable detail. However, it involves a reformulation of manifold theory at the most
fundamental level, so mathematicians infected with certain viruses of tradition may find it
hard to swallow.
"The differentiable manifold is rightly recognized as the general arena for differential and integral calculus. Unfortunately, the conventional definition of "manifold" is couched in terms of coordinates, and this makes the calculus coordinate dependent at its foundations, so much fussing about is needed to derive invariant structures.
In contrast, Geometric Calculus makes it possible to dispense with coordinates and deal with invariants exclusively.
"The key idea is to impose algebraic structure on a manifold by regarding the points as vectors obeying the rules of Geometric Algebra for addition and multiplication. This algebraic structure is then used, instead of coordinates, to define the intrinsic structure of the manifold. A manifold defined in this way is called a vector manifold, though it is claimed to be essentially equivalent to the conventional definition of manifold.
In some quarters, the very suggestion that manifolds might be defined without the elaborate system of charts and atlases in conventional manifold theory provokes spasms of mathematical outrage reminiscent of the initial response among mathematicians to Dirac's delta function.... "The task remains for some ambitious young mathematician to produce a fully rigorous treatment of vector manifold theory.
"An alternative treatment of differentiation and integration on vector manifolds with much to recommend it is given by Sobczyk in [his book on Clifford Algebra and Electromagnetics]. Sobczyk limits his treatment to manifolds embedded in Euclidean space, but a cursory examination of his paper reveals that his formulation of the basics makes no appeal to any embedding assumption and so is applicable to vector manifolds in all generality.
"One of the "knee-jerk" objections to the vector manifold concept is the unsubstantiated claim that it is less general than the conventional manifold concept. Two arguments have been proffered in support of this claim. Both are wrong .... The first argument holds that the very use of geometric algebra presumes an embedding of the manifold in a vector space. The mistake implicit in this argument is the tacit assumption that the necessary algebraic structure can only be defined in terms of a basis, which, of course, also determines a vector space. Here again the coordinate virus is at work! Again, the antidote is to realize that addition and multiplication of points can be defined abstractly without assuming closure under addition and scalar multiplication, that is, without assuming that the points generate a vector space of some finite dimension.
"Thus, embedding spaces are not presumed in vector manifold theory. On the contrary, geometric calculus may be the ideal tool for proving the known embedding theorems and possibly for discovering new ones.
"The second mistaken argument against vector manifold theory holds that the theory is limited to metric manifolds, so it is less general than conventional manifold theory. Attentive readers will recognize the quadratic form virus at work here! It is true that Geometric Algebra automatically defines an inner product on the tangent spaces of a vector manifold. But we have seen that this inner product can be interpreted projectively and so need not be regarded as defining a metric. Moreover, our earlier considerations tell us that the inner product cannot be dispensed with, because it is needed to define completely the relations among subspaces in each tangent space.
"On the other hand, it is a well-known theorem that a Riemannian structure can be defined on any manifold. Possibly this amounts to no more than providing the inner product on a vector manifold with a metrical interpretation, but that remains to be proved.
For modeling the spacetime manifold of physics, vector manifold theory has many advantages over the conventional approach. For the spacetime manifold necessarily has both a pseudoRiemannian and a spin structure. To model these structures the conventional "modern" approach builds up an elaborate edifice of differential forms and fibre bundles, whereas vector manifolds generate the structure as needed almost automatically.
"Moreover, only geometric calculus provides a common mathematical language that smoothly articulates all branches of physics from relativistic and quantum mechanical to nonrelativistic and classical. The vector manifold concept is needed to formulate all this in a coordinate-free way."
An orthogonal transformation, R, is DEFINED BY CONDITION OF LEAVING INNER PRODUCT INVARIANT: (Ra)·(Rb) = a · b. It is a rotation if det R = 1, that is, R(En, n) = En, n, where En, n is the UNIT PSEUDOSCALAR for vector space, Vn, n. Rotations form the special orthogonal group, SO(n, n).
In MULTIVECTOR THEORY, EVERY ROTATION TAKES THE CANONICAL FORM, Ra = RaR†, for EVEN MULTIVECTORS ("ROTORS") satisfying RR† = 1. The rotors form a mulltiplicative group, the spin group, Spin(n,n), a spin representation of special orthogonal group, and a double covering of it, since both both ±R correspond to the same R.
EVERY BIVECTOR DETERMINES A UNIQUE ROTATION. The bivector generators of a rotation or spin group form a Lie Group under the commutator product -- reducing the description of Lie Groups to that of Lie Algebras.
In general, it can be shown that many classical groups can be classified as stability groups of various involutory bivectors -- a simpler and more systematic approach than the traditional one. So one systematically searches for involutory bivectors and invariant relations for them. Since all groups are subgroups of an orthogonal group, O(p,q), the inner product is always available as an invariant form, and the psuedoscalar, Ep, q, is necessarily invariant. So, you search for involutory bivectors in vector space, Vp, q.
The American mathematical physicist, A. Barut, commented in 1985: "Because the representation of a Clifford algebra coincides with the fundamental representation of the spin group, we could, and we generally do, also describe the particle multiplets by the the spin representations of the orthogonal Lie groups or by their Lie algebras. Also the complete set of commuting operators can be chosen to be the same in both cases. However, the Lie group has infinitely many representations which must all occur in nature if the symmetry is fundamental, but the Clifford algebra has only one representation. Moreover, there is no internal space on which the continuous Lie group acts....[T]hese and other considerations favor the Clifford algebras as internal symmetry operations and not the Lie groups."
Given two of the three special "Clifford products" -- namely, INNERPRODUCT and OUTERPRODUCT -- I UNIQUELY DERIVE (the 3rd of them) MULTIPRODUCT, their sum.