Topology studies properties of objects which preserved under deformations, twistings, stretchings. Thus, a circle is topologically equivalent to an ellipse, since it can be deformed thus by stretching. A sphere is topologically equivalent to an ellipsoid, for similar reasons. Etc.
Initiated by the great Swiss mathematician, Leonhard Euler (x-y), topology initially studied curves, surfaces, and other 2-D and 3-D structures, treating these structure "in their own right", independently of their embedment in space.
Properties not destroyed by deforming, twisting, stretching are properties preserved by a homeomorphic trnsformation. (The geometric property of isotopy -- meaning same properties in any direction - is tested by distorting embedded sutructures, invoking the extrinsic ("contextual") property of "embedment". But homeopmorphism is intrinsic, not requiring a "context".)Homeomorhism (a.k.a. topological transformation: A 1-1 mapping from set A to set B such that any open set in A maps into an open set in B. (Failure would mean "having to go outide or cross a boundary".)
Topology is subdivided into algebraic topology (a.k.s. combinatorial topology), differential topology, and low-dimensional topology.
A topology can be formally defined in terms of set-theoretic operations. A set X, together with a collection C of subsets is a topology if, and only if, the subsets in C obey the following properties:
- C contains the (trivial) subsets X and the empty set;
- If sets A and B are in C, then so is their union and intersection.
The city of Könisberg, East Prussia (now known as Kaliningrad, Russia) is located on the Pregel River which contains two islands connected by bridges (shown below). In the 18th century, the famous German philosopher, Immanuel Kant (x-y), often sat a a table outside a tavern beside River Pregel, drinking beer and talking. Sometimes Kant and his cronies wondered how a person could traverse all of the Künisberg Bridges without traversing one of them twice . (As a geometric figure, this means that the path can be drawn completely without removing pen or pencil from the paper -- "unicursally".)
Later, Euler, at the Russian Court of Empress Catherine the Great, heard of this problem
and solved it by studying the edges of the bridge-figure, which (abstractly)
mathematicians call a "graph" or "network".
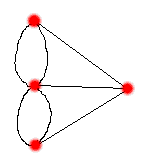
Euler noted that the vertices of its edges are all odd in number (3, 3, 3, 5). Euler
proved that ANY NETWORK (GRAPH) WITH MORE THAN 2 ODD VERTICES CANNOT BE TRAVERSED COMPLETELY
WITHOUT TRAVERSING AT LEAST ONE EDGE TWICE. Hence, the question of Kant and friends has the
answer "No!". Euler also proved that ANY NETWORK (GRAPH) WITH ZERO ODD VERTICES CAN BE TRAVERSED
UNICURSLLY WITH RETURN TO STARTING POINT. A well-known example of this is the famous regular
five-point star.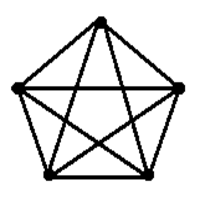
(Please see www.geocities.com/jok104/.)
(The science-fiction writer, Cyril Kornbluth, composed a limerick about the the Möbius strip:
A burleyque dancer, a pip
Named Virginia, could peel in a zip;
But she read sciencefiction
And died of constriction
Attempting a Moebius strip.
You find this in Fantasia Mathematica, Ed. Clifton Fadiman, as well as a science-fiction
story, "A Subway Named Moebius". In August, 1966, R. L. Davis was granted a patent -- 3,267,406 --
for a "non-inductive electrical resistor", shaped as a Möbius band.)- denote vertices of a topological structure by V;
- denote edges by E;
- denote faces by F;
- then a topological structure has a measure: c = V - E + F.
(Our greatest American scientist, Josiah Willard Gibbs (1839-1903) -- called "Father of the American Chemical Industry" -- derived (from the Eulerian charcteristic) "the Gibbs phase rule", a formula for ascertaining the portion of a chemical distributed in the gaseous, liquid, and solid states.)
Any topological structure can be described as a sphere with zero or one or more holes, zero or one or more "handles" (cylinders), and zero or one or more "crosscaps" (möbius construction in 4-D).