ABRIDGED HISTORY OF TOPOLOGY
Subject began with the 1736 paper, Solutio problematis ad geometriam situs pertenentis
(The aolution of a problem relating to the geometry of position), by Leonard Euler (1707-83)
on the Könisberg Bridge problem: 
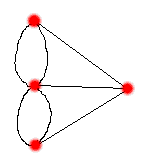 a
river flowing through the town of Könisberg was spanned by seven pridges, and the problem
concerned the possibility of crossing all seven bridges without crossing one of them twice.
The struture involved is now known as a graph, and Euler proved the following (in modern
mathematical languge): a graph has a path traversing each edge exactly once if exactly two
vertices of the graph have exactly two odd vertices. Since the above graph has four vertices, and each is odd (four odd vertices), the
theorem explained why the problem has no solution. Euler's title showed that he had set forth
a new subject, which was long known as "Analysis Situs" (analysis of position). (Note: If a graph
has zero odd vertices, it can not only be traversed with repetition, but also by a path
returnng to the starting point, that is, the path is unicursal. This is the case with the
familiar five-point star (only two-vertices and four-vertices), which can be drawn
without taking the pencil from the paper and the drawing returns to the starting point.)
Also, in advancing mathematics beyond measurement, Euler (1750) stated a formula
for convex polygons ("Euler characteristic"), in terms of the number of polygonal vertices
, V, the number of polygonal edges, E
. amd the number of polygonal faces, F:
V - E + F = 2. His 1752 proof dissected solids into tetraheadral slices, but
assumed the polygons are convex (any line segment connecing two points within the polygon
also lies within the polygon).
In 1813, Antoine-Jean Lhuilier (1750-1840) showed that Euler's formula is incorrect for a
polygon with holes; given G holes: V -
E + F = 2 - 2G. (This is the first statement of a topological invariant. A t.i. is
a property of a topological space which is shared by any space topologically equivalent
or homeomorphic to it, meaning any map from an open set of one space to the other space
corresponds to a point in an open set of the latter. Familiar examples include
non-algebraic invariants, such as compactness, coonnectedness, Haussdorfness. Euler
characteristic, orientability, dimension and algebraic invariants such as homology
groups, homotopy groups, and k-theoyr.)
In 1865, Augustin Möbius (1790-1848) showed that aa band of paper, when twisted and
glued together, constitutes the one-sided nonorientable surface now known as a
Möbius strip or band or Möboid. (Möbius proved it cannot be filled with
compatibly oriented triangles.) Johann Benedict Listing (1802=1882) -- first to use the word
"topology" -- discovered and described the möboid in 1847.
Bernard Riemann (x-y) studied conectivity of surfaces, introducing (1857) Riemann
surfaces in complex function analysis: since, given the polynomial equation,
f(w,z), its roots vary with w, z. on
Riemann surfaces determined by f(w,z), the function
w(z) = 0 is single-valued.
Camille Jordan (1838-1922) introduced another procedure for analyzing the connectivity of
a surface:
a
river flowing through the town of Könisberg was spanned by seven pridges, and the problem
concerned the possibility of crossing all seven bridges without crossing one of them twice.
The struture involved is now known as a graph, and Euler proved the following (in modern
mathematical languge): a graph has a path traversing each edge exactly once if exactly two
vertices of the graph have exactly two odd vertices. Since the above graph has four vertices, and each is odd (four odd vertices), the
theorem explained why the problem has no solution. Euler's title showed that he had set forth
a new subject, which was long known as "Analysis Situs" (analysis of position). (Note: If a graph
has zero odd vertices, it can not only be traversed with repetition, but also by a path
returnng to the starting point, that is, the path is unicursal. This is the case with the
familiar five-point star (only two-vertices and four-vertices), which can be drawn
without taking the pencil from the paper and the drawing returns to the starting point.)
Also, in advancing mathematics beyond measurement, Euler (1750) stated a formula
for convex polygons ("Euler characteristic"), in terms of the number of polygonal vertices
, V, the number of polygonal edges, E
. amd the number of polygonal faces, F:
V - E + F = 2. His 1752 proof dissected solids into tetraheadral slices, but
assumed the polygons are convex (any line segment connecing two points within the polygon
also lies within the polygon).
In 1813, Antoine-Jean Lhuilier (1750-1840) showed that Euler's formula is incorrect for a
polygon with holes; given G holes: V -
E + F = 2 - 2G. (This is the first statement of a topological invariant. A t.i. is
a property of a topological space which is shared by any space topologically equivalent
or homeomorphic to it, meaning any map from an open set of one space to the other space
corresponds to a point in an open set of the latter. Familiar examples include
non-algebraic invariants, such as compactness, coonnectedness, Haussdorfness. Euler
characteristic, orientability, dimension and algebraic invariants such as homology
groups, homotopy groups, and k-theoyr.)
In 1865, Augustin Möbius (1790-1848) showed that aa band of paper, when twisted and
glued together, constitutes the one-sided nonorientable surface now known as a
Möbius strip or band or Möboid. (Möbius proved it cannot be filled with
compatibly oriented triangles.) Johann Benedict Listing (1802=1882) -- first to use the word
"topology" -- discovered and described the möboid in 1847.
Bernard Riemann (x-y) studied conectivity of surfaces, introducing (1857) Riemann
surfaces in complex function analysis: since, given the polynomial equation,
f(w,z), its roots vary with w, z. on
Riemann surfaces determined by f(w,z), the function
w(z) = 0 is single-valued.
Camille Jordan (1838-1922) introduced another procedure for analyzing the connectivity of
a surface:
- a simple closed curve ("Jordan curve") separates space into exactly two parts,
namely, inside and outside the curve;
- a Jordan curve on a surface is irreducible if cannot be transformed into a point
if a general circuit, c, can be transformed into a system
of irreducible circuits, a1, a1, ..., an
, so that mi counts occurrences of ai in circuit c, then c =
m1a1 + m1a1 + ... + mnan.
- a circuit is irreducible if, and only if, c = m1a1
+ m1a1 + ... + mnan = 0;
- a system of irreducible circuits, a1, a1,
..., an, is independent if, and only if, the previous vanishing
condition does not exist;
- such a system is independent if, and only if, any cicuit can be expressed in terms
of them;
- Jordan proved that the number of circuits in a complete independent set is a
topological invariant of the surface.
In 1871, Enrico Betti (1823-92) published a memoir on topology which included what are now
labeled "Betti numbers", so named by Henri Poincaré (x-y), who was inspired to work in
topology by Betti's work. Betti introduced coonectivity numberts for each dimension,
1, 2, n - 1:
- 1-D connectivity number: number of nonbifurcateable closed curves which can be drawn in a
structure;
- 2-D connectivity number: number of (2-D) closed surfaces in a structure which do not bound
a 3D-region of the structure;
- higher dimensional connectivity numbers are similarly defined;
- the closed curves, surfaces, and higher-dimensinal figures involved in this analysis are
called "cycles".
Poincaré assumed a space is triangulable, i.e., dissectable into
triangles, entirely sharing each triangular side with two adjacent triangles. A triangle is
an instance of a 1-simplex, a notion introduced by L. E. J. Brouwer (1881-1966). So
Poincaré treated space as what is now called a simplicial complex (also from
Brouwer). For each dimension of possible simplexes in a complex, P. defined the number of
independent cycles of that dimension as the Betti number of that dimension. Given a
manifold, M, with various manifolds, mi
, mapped to M. In P.'s work:
- the manifolds, mi, form a homology when they
form the oriented boundary of a higher-dimensional manifold inside ofthe
k-th homology group M;
- given a complex, Ck, one can form Eki, a linear combination of its k
-dimensional oriented simplexes s.t. Ck = c1
Ek1 + c2Ek2 + ... + cnE
kn (for positive or negative integers, c
i, labeled a chain, and a chain with boundary zero is a cycle
, so some chains are cycles. P. also introducted torsion coefficients to provide for
the condition that (say, in the projective plane) a cycle does not bound but twice the
cycle does bound. (P.'s treatment resembles modern cobordism.) Eventually P.'s
homology was replaced by the more general singular homology.
In 1890, Guiseppe Peano (1858-1932) showed that Jordan's curve theorem was "too broad" by
showing that a curve fittting his definition can run throgh all points of a square at least
once, thereby filling a plane section. This "Peano curve" is neither continuoous
nor single-valued.
Oswald Veblen (1880-1960) and James W. Alexander (1888-1971) replaced an oriented
simplex by an unoriented one with coefficients modulo 2; also
coefficients modulo m for chains and cycles. Lev S.
Pontrjagin (1908-1960) replaced these by elements of an Abelian group.
during 1925-30, many mathematicians, inluding Emmy Noether (x-y), recast tht thory of
chains, cycles, bounding cycles in terms of group theory:
- chains and cycles can be added by summing coefficients of the same simplex, forming
Abelian groups, Ck(K);
- the relation of chain to boundary becomes a homomorphism from Ck(K) (the group of k-dimensional
chains) into a particular subgroup, Hk-1, of
the group, Ck-1(K), of k-1-
dimensional chain.
- the set of all k-cycles k > 0
is a subgroup, Zk(K), of
Ck(K), and, under the above homomophism, this goes into the identity
element (0) of Ck-1(K).
Since every chain is a cycle, Hk-1 is a subgroup
of Zk-1(K).
- then:
- for any k
 0, the factor group of Zk(k) -- i.e., the k-dimensional
cycles, modulo the subgroup, Hk(k), of the bounding
cycles -- is the k-th homology group of K and denoted, Bk(K);
0, the factor group of Zk(k) -- i.e., the k-dimensional
cycles, modulo the subgroup, Hk(k), of the bounding
cycles -- is the k-th homology group of K and denoted, Bk(K);
- the number of linearly independent generators of this factor group is the k-th Betti number of the complex, denoted pk
(k);
- the k-th homology group may also contain finite cyclic
groups, corresponding to the torsion groups, and the orders of these finite groups are the
torsion coefficient.
TOPOLOGY IN CONVERGENCE PROCESS IN ANALYSIS AND POINT SET TOPOLOGY
- In 1817, Bernhard Bolzano (1781-1848), removed convergence from sequences of
numbers to associate convergence with any inbounded subset of the real numbers.
- In 1871, Georg Cantor (1845-1918)
- introduced the first derived set or set of limit points;
- defined closed sets of the real line as sets containg their first derived set;
- introduced the concept of the open set, critical in point set topology.
- In 1877, Karl Weierstrass (1815-1897) rigorously proved the Bolzano-Weierstrass Theorem
: A bounded infinite subset, S, of the real numbers possesses at
least one point, p, of accumulation -- that is, p
satisfies the property that, given any
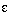 >
0, there exists an infinite sequence, {pn},
of points of S with |p - pn|
<
>
0, there exists an infinite sequence, {pn},
of points of S with |p - pn|
< 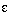 . This introduced neighborhood of a point.
. This introduced neighborhood of a point.
- In 1906, Maurice Fréchet (1878-1973)
- defined a space as compact if any infinite bounded subset contains a point of
accumulation;
- defined the concept of a metric;
- extended Cantor's concepts of open and closed set to metric spaces.
- In 1909, Friedrich Riesz (1880-1956) disposed of the metric concept for a new
axiomatic treatment of topology based upon a set definition of limit points.
- In 1914, Felix Hausdorff (1868-1942) defined neighborhoods by four axioms, without
metric reference.
- The work of Riesz and Hausdorff allows definition of abstract topological spaces.
TOPOLOGY IN FUNCTIONAL ANALYSIS
This originated in problems both in physics and astronomy.
- Jacob Bernoulli (1654-1703) and Jacob Bernoulli (1667-1748) invented the calculus of
variations, in which there developed the notion of a functional wherein the value
of an integral is a function of the functions being integrated.
- in 1903, Jacques Hadmard (1865-?) introduced the term "functional" in studying linear
functionals, F, of the form:
F(f) = lim  f(x)gn(x)dx,
f(x)gn(x)dx,
for lim 
 , with integral from
a to b.
, with integral from
a to b.
- In 1904 Fréchet defined the derivative of a functional.\
- In 1907, Erhard Schmidt (1876-1959) studied the notion of convergence in sequence spaces
, and defined distance in terms of inner products.
- In 1932, Stefan Banach (1892-1945) shifted from inner product spaces to normed
spaces, showing that Fréchet's linear functions had a natural setting in normed

 a
river flowing through the town of Könisberg was spanned by seven pridges, and the problem
concerned the possibility of crossing all seven bridges without crossing one of them twice.
The struture involved is now known as a graph, and Euler proved the following (in modern
mathematical languge): a graph has a path traversing each edge exactly once if exactly two
vertices of the graph have exactly two odd vertices. Since the above graph has four vertices, and each is odd (four odd vertices), the
theorem explained why the problem has no solution. Euler's title showed that he had set forth
a new subject, which was long known as "Analysis Situs" (analysis of position). (Note: If a graph
has zero odd vertices, it can not only be traversed with repetition, but also by a path
returnng to the starting point, that is, the path is unicursal. This is the case with the
familiar five-point star (only two-vertices and four-vertices), which can be drawn
without taking the pencil from the paper and the drawing returns to the starting point.)
a
river flowing through the town of Könisberg was spanned by seven pridges, and the problem
concerned the possibility of crossing all seven bridges without crossing one of them twice.
The struture involved is now known as a graph, and Euler proved the following (in modern
mathematical languge): a graph has a path traversing each edge exactly once if exactly two
vertices of the graph have exactly two odd vertices. Since the above graph has four vertices, and each is odd (four odd vertices), the
theorem explained why the problem has no solution. Euler's title showed that he had set forth
a new subject, which was long known as "Analysis Situs" (analysis of position). (Note: If a graph
has zero odd vertices, it can not only be traversed with repetition, but also by a path
returnng to the starting point, that is, the path is unicursal. This is the case with the
familiar five-point star (only two-vertices and four-vertices), which can be drawn
without taking the pencil from the paper and the drawing returns to the starting point.)
 0, the factor group of Zk(k) -- i.e., the k-dimensional
cycles, modulo the subgroup, Hk(k), of the bounding
cycles -- is the k-th homology group of K and denoted, Bk(K);
0, the factor group of Zk(k) -- i.e., the k-dimensional
cycles, modulo the subgroup, Hk(k), of the bounding
cycles -- is the k-th homology group of K and denoted, Bk(K);
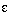 >
0, there exists an infinite sequence, {pn},
of points of S with |p - pn|
<
>
0, there exists an infinite sequence, {pn},
of points of S with |p - pn|
<  f(x)gn(x)dx,
f(x)gn(x)dx,
 , with integral from
a to b.
, with integral from
a to b.