("DIE MATHEMATIK HINTER DEM RÄTSEL DES SÜSSIGKEIT GEIZHALS")

Mathematiker und Studenten verwenden heute ausführlich das richtige Dreieck in
Geometrie und Trigonometrie, die die "Pythagoräische Formel" benutzen, Längen von den SEITEN
des Dreiecks (a, b) zu erzählen, und DIAGONAL(c
): a2 + b2 = c2. Jedoch, hat
Pythagoras diese Formel nicht entdeckt, aber hat offensichtlich es in seinem
 durch Ägypten und Mesopotamien gelernt reist.
Dennoch Zahl Drillinge {a,b,c} passend der Formel -- zum Beispiel,
{3, 4, 5}, {5, 12, 13} usw --- Sind heute "Pythagoräische Drillinge"
beschriftet. Hier ist was wir von diesem Thema, und seinen Folgen wissen.
durch Ägypten und Mesopotamien gelernt reist.
Dennoch Zahl Drillinge {a,b,c} passend der Formel -- zum Beispiel,
{3, 4, 5}, {5, 12, 13} usw --- Sind heute "Pythagoräische Drillinge"
beschriftet. Hier ist was wir von diesem Thema, und seinen Folgen wissen.
Kenntnis von ägyptischer Mathematik leitet von zwei Artefakten, Der
Rhynd Papyrus ab (hat genannt für seinen Spender Zum britischen Museum) und Das Moskau
Papyrus (Jetzt in Museum von Belegt mit einer Geldstrafekünste, Moskau, Russland). Beide
leiten offensichtlich von einer Periode zwischen 2000 B. C ab. und 1580 B. C. Sie beschreiben
Fähigkeit, linear (zuerst Grad) Gleichungen in einem unbekannten zu lösen, aber kein Beweis die
zweiten Gradegleichungen von der Lösung oder Formeln wie zum Beispiel "Der Pythagoräer". Die
Ägypter behandeln Bruchteile durch Hinzufügeneinheitenbruchteile, wie zum Beispiel 1/2, 1/3, 1/4, 1/5 usw. (Amerikaner benutzen "ägyptische Bruchteile" beinahe jeden
Tag -- in "machend Änderung in gewerblichen Verhandlungen". Folglich ein
penny = $1/100; ein mickel = $1/20; ein dime = $1/10; ein quarter = $1/4; a Fünfzig Cent Stück =
$1/2.) Später werden wir sehen, wie der "ägyptische Bruchteil" Format zur besten Prüfung
der Irrationalität von Zahlen ausdehnt.
Zirka 450 B.C., Parminides von Elea haben die Pythagoräischen Ideen von Vielfältigkeit und
Änderung mit Einigkeit und Ständigkeit herausgefordert, die sogar argumentieren, daß die
Änderungen und winkt wir sehen in die Welt ILLUSORISCH sind. Parmenidesanhänger, Zeno formuliert
die seine Paradoxa weiter herauszufordern Pythagoräische digitale Geometrie und ZAHL ALS
GRÖSSE, erend GEOMETRISCHE EINHEITEN für diesen Zweck reservi
Im 420 B.C. ist Hippias (460-400 B.C., Pythagoräischer Anhänger), die Unmeßbarkeit von der
Quadratwurzel von zwei entdeckt zu haben, und gesagt Beweis von dies gegeben zu haben.
Sie zirka 390 B.C., Pythagoräischer Gelehrter und Student von Hippias, Theatetus (beschrieben
durch Platon in Dialog durch, daß) nennt, lehren ungefähr "Unmeßbarkeit". Auch gelehrt durch
Theodorus von Cyrene.
Zirka 365 B.C., Eudoxus (c. 408-355 B.C.) -- Bedacht mit Archimedes
Verursachend eine 1900 jährige Vernachlässigung theoretischer Mechaniker in Europa, "Die
Industrielle Revolution" und Ausdehnensklaverei verschiebend.
Eudoxus auch hat geschaffen die geometrische Methode von Erschöpfung, wobei, zum Beispiel, eine
Reihenfolge von Polygone von wachsenden Seiten kann ausschöpfen (oder kann nähern der Struktur
von) der Kreis. der der. (Dies erwartet "den wesentlichen Nierenstein" im 17. Jahrhundert -- und
ein Schritt nach Rechtfertigung Pythagoräischer Arithmetik).
Zirka 300 B.C., in Alexandria, haben Ägypten, griechisch Euclid (450-380 B.C.) seine Elemente
der Geometrie herausgegeben,
Im großen Alexandrian Periode (332 B.C.-420 n. Chr.) erschreckend Dämpfeautos, werden gerollt
die die Straßen und die riesigen Roboter Arme unter Dampfantrieb hinunter bewegt haben, das
treue. Kaiserliche Römeringenieure haben entwickelt wirksamen Wind fräst und bewässert Mühlen
(zum Beispiel, im ersten Jahrhundert B.C., der römische Ingenieur Vitrivius hat beschrieben das
unter Schußwasserrad, später so nützlich in mittelalterlichem und aufstellt mittelalterlichem
Europa, noch selten benutzt durch Römer) ist das. Diese wirksamen Wässermühlen und Windemühlen
hätten die Sklavenarbeit von der Zeit ersetzen können. Aber ohne theoretische Mechaniker,
dieses zu zeigen, und Hoffnung der Verbesserungen, Sklaverei zu geben, die in Europa für
Hunderte von mehr Jahren fortgesetzt werden.
Im 415 n. Chr., in Alexandria, Ägypten, pöbelt Christ ermordeten Hypatia
Einer war der größte der Astronom Mohammed ibn Musa Al-Khowarizmi (zirka 825 A.S.)
Der wichtigste islamische Fortschritt sollte Bewegung in Arithmetik formulieren und
sollte herausfordern der Aristotlean "Gesetz von Fallenkörpern". Eigentümlich haben Islamische
Argumente für Bewegungsarithmetik von Analogien in Apotheke und optisch abgeleitet.
Es ist möglich erschienen, Größen in Medizin zu ändern, und in leichten Intensitäten deshalb dies
wurde ausgedehnt, zu winken.
In dies "Mittelalterliche Renaissance" Periode, haben arabische Künstler in der geometrischen
Kunst von figrative Verzierung ausgezeichnet sich. Das feinste Beispiel für dies ist Der
Alhambra in Grenada (Spanien), ein fortess und Palast. Mathematiker erkennen 128 abgesonderte
Muster von "dem Tapetentilegroup". Alle von diesen erscheinen in den Dekorationen Dem Alhambra
(als in einem Alhambra Portal Oder ein (Erleichterung)
Alhambra Erleichterung oder ein
Alhambra Mosaik).
Als Sie in Der Mittelalterlichen Maschine: Die Industrielle Revolution
das das Mittelalter lesen können, durch Jean Gimpel, 1977, hat im 12. Jahrhundert (n. Chr.)
begonnen, was "Die Mechanische Industrielle Revolution" gerufen werden sollte. Mönche --
wünschend, ihre Speise und andere Bedürfnisse zu erheben, hat noch Zeit für Gebet und tiefes
Nachdenken -- besondere Erlaubnis durch den Papst, heidnische Texte zu lesen, wie zu zeigen,
Wässermühlen zu bauen, und Windemühlen wurden gegeben. Im 12. Jahrhundert und das nächste, diese
Mühlen breiten über Europa aus. (Das Domesday Buch die 1086 Listen vom Jahr 5624 Wasserräder
haben Mühlen in England Süden von Trent, oder um eine Mühle für jede 400 Personen getrieben).
Deutlich hätte weitere Verlängerung von diesen Mühlen dann beseitigt viel von der Sklavenarbeit
Existieren, aber "die Lektion" war noch nicht offensichtlich genug.
William von Ockam (1280?-1349?), hat die Ahnung der Trägheit, eines physischen Begriffs
skizziert, die später zu Newton kreditiert worden sind. (Der charactor von William von
Baskerville, der von Sean Connery im Film, Dem Namen von der Rose, gespielt worden ist,
wurde nach Ockam entworfen). Jean Buridan (1295?-1359), französischer Philosoph, in 1350er
jahren hat die Ahnung des Anstoßes entwickelt, schließt ein physischer Begriff zum Begriff des
skizziert In 1320 n. Chr., Thomas Bradwardine (1290-1349)., der
an Merton Hochschul Oxford studiert hat, ist Kanzler der Str. geworden. Der Dom von Paul.
Bradwardine war ein berühmter Mathematiker sowie Theologe, bekannter als "der tiefschürfender
Doktor". Umgehung beide das Platonische und Aristotlean Traditionen, hat Bradwardine Körper in
einheitlicher Bewegung und Verhältnissen der Geschwindigkeit im Traktat De proportionibus
velocitatum in motibus (1328) studiert. Bradwardine war einer "Oxford Taschenrechner" der,
von Merton Hochschule, Oxford Universität, studierend Mechaniker mit William Heytesbury, Richard
Swineshead, und Johns Dumbleton. Der Oxford Taschenrechner haben Kinematik von "dynamisch"
unterschieden, betonend Kinematik, und, "unmittelbare Geschwindigkeit" untersuchend. Sie haben
zuerst das formuliert "bedeutet Geschwindigkeitlehrsatz: ein Körper, der mit beständigen
Geschwindigkeitenreisen bewegt, distanziert und messen Zeit gleich einem beschleunigten Körper,
dessen Geschwindigkeit halb die endgültige Geschwindigkeit vom beschleunigten Körper ist". Sie
haben auch diesen Lehrsatz vorgeführt -- Substanz von "Das Gesetz von Fallenkörpern" -- lang,
bevor Galileo mit dies kreditiert ist. In "Tractatus de proportionibus" (1328) hat ausgedehnt
Thomas Bradwardine Eudoxus "Theorie der Verhältnisse", den Begriff von "Exponentialwachstum" zu
erwarten, später entwickelt durch die Bernoullis und die Euler, mit "Zinseszinsen" als ein
Sonderfall. Bradwardine ist Erzbischof von Canterbury in 1349 geworden aber ist gestorben, ein
Monat später, von der Schwarzen Plage. Bradwardine ist (als "Bisshop Bradwardyne") in Chaucer
erwähnt Canterbury Erzählungen, In "die Erzählung Des Nonne Priesters", Linie 476.
Ausbildung war mündlich gewesen. Die Kirche hat mehr Generalvorlesung heidnischer Bücher jetzt
erlaubt, leitend Die Renaissance ein. (Erzählen diese Geschichte zu jugendlichagers der "will
arbeiten mit ihren Händen", aber fragen warum sie haben gelesen Fähigkeiten!)!
Chronologie, Fortsetzt.
 Die Pythagoräische Formel wurde entdeckt zirka
2000 B. C. in Babylonia oder Ägypten oder beiden. Wir wissen um seinen Babylonian Ursprung von
ungefähr Hälfte von einen Millionen Tonen Babylonian Tabletten sind eingeschnitten worden in
ihrer geschriebenen keilförmigen Schriftart, ist ausgegraben worden seit der ersten Hälfte vom
19. Jahrhundert (haben ausgestellt in den großen Museen von Paris, Berlins und London sowie den
archäologischen Ausstellungen an Yale, Kolumbien und die Universität von Pennsylvanien).
Etwa 400 von den Tabletten führen mathematische Probleme und mathematische Tische auf. Sie
zeigen, zum Beispiel, daß Babylonian Priester gehabt haben Ein iterativer Algorithmus zum
Finden von squareroots von allen Zahlen -- Einschließlich der Quadratwurzel von 2 -- zu
irgendeiner gewünschten Annäherung.
Die Pythagoräische Formel wurde entdeckt zirka
2000 B. C. in Babylonia oder Ägypten oder beiden. Wir wissen um seinen Babylonian Ursprung von
ungefähr Hälfte von einen Millionen Tonen Babylonian Tabletten sind eingeschnitten worden in
ihrer geschriebenen keilförmigen Schriftart, ist ausgegraben worden seit der ersten Hälfte vom
19. Jahrhundert (haben ausgestellt in den großen Museen von Paris, Berlins und London sowie den
archäologischen Ausstellungen an Yale, Kolumbien und die Universität von Pennsylvanien).
Etwa 400 von den Tabletten führen mathematische Probleme und mathematische Tische auf. Sie
zeigen, zum Beispiel, daß Babylonian Priester gehabt haben Ein iterativer Algorithmus zum
Finden von squareroots von allen Zahlen -- Einschließlich der Quadratwurzel von 2 -- zu
irgendeiner gewünschten Annäherung.
In der Abwesenheit mathematischen Mittels von Untersuchungsbewegung die
Ideen des Philosophen
Zirka 540 B.C.: Besitzdauer von Pythagoras (580-496 B.C.) in Crotona, lehrend diese Formel,
zusammen mit seiner digitalen Geometrie, die (inbegriffen) Freudenzahl ALS GRÖSSE
(Vielfältigkeit der Dinge), von sowohl PLATZ als auch ZEIT. Das "Problem vom Tor" aufgeregte
Pythagoräische Mathematik und hat seinen philosophischen Feinden Stütze gegeben.
 (287-212 B.C.) als "größten alte Mathematiker" --
gelehrt in Platon Schule daß GRÖSSE nur sollte definiert werden GEOMETRISCH und sollte geschaffen
werden ein Verhältnis von Größen und einem Verhältnis, die haben verstanden beide einstimmenden
und unmeßbaren Verhältnisse (erwartet die Arbeit von 18. und 19. Jahrhundert Mathematikern). die
der von der, Diese LED zu 2000 Jahren von Herrschaft von MATHEMATIK durch GEOMETRIE. Und LED
Platon zu argumentieren, daß das, das arithmetisch unmeßbar proklamiert, jene Bewegung besagt,
("Geometriesatz messen Zeit") kann in Arithmetik nicht formuliert werden -- bedeutend keine
Maßnahme der Geschwindigkeit, Beschleunigung, Kraft usw.
(287-212 B.C.) als "größten alte Mathematiker" --
gelehrt in Platon Schule daß GRÖSSE nur sollte definiert werden GEOMETRISCH und sollte geschaffen
werden ein Verhältnis von Größen und einem Verhältnis, die haben verstanden beide einstimmenden
und unmeßbaren Verhältnisse (erwartet die Arbeit von 18. und 19. Jahrhundert Mathematikern). die
der von der, Diese LED zu 2000 Jahren von Herrschaft von MATHEMATIK durch GEOMETRIE. Und LED
Platon zu argumentieren, daß das, das arithmetisch unmeßbar proklamiert, jene Bewegung besagt,
("Geometriesatz messen Zeit") kann in Arithmetik nicht formuliert werden -- bedeutend keine
Maßnahme der Geschwindigkeit, Beschleunigung, Kraft usw. Aristotle(384-322 B.C.) hat
Dominanz in Physik, besonders seiner gewonnen "Gesetz von Fallenkörpern" : ein Objekt ist zur
Erde gemäß sein Gewicht -- das schwerer der Körper, das schneller der Körper fällt gefallen. Im
Verlauf der Jahrhunderte hat ein paar skeptisches einzeln gezeigt auf ein Paradoxon in dieser
Ahnung. Gegeben ein Zwei Einheitgewichtobjekt und ein Eineinheitgewichtobjekt, das erste soll,
durch dieses Gesetz fällt viel schneller als die Sekunde (numerische Verhältnisse wurden
ignoriert). Gebunden zusammen, das Drei Einheitgewichtobjekt soll SCHNELLER als das Zwei
Einheitgewichtobjekt, aber -- gleichzeitig fallen -- LANGSAMER, da das Eineinheitgewichtobjekt
zurück das Zwei Einheitgewichtobjekt halten soll. Aber solche Argumente wurden ignoriert.
Aristotle(384-322 B.C.) hat
Dominanz in Physik, besonders seiner gewonnen "Gesetz von Fallenkörpern" : ein Objekt ist zur
Erde gemäß sein Gewicht -- das schwerer der Körper, das schneller der Körper fällt gefallen. Im
Verlauf der Jahrhunderte hat ein paar skeptisches einzeln gezeigt auf ein Paradoxon in dieser
Ahnung. Gegeben ein Zwei Einheitgewichtobjekt und ein Eineinheitgewichtobjekt, das erste soll,
durch dieses Gesetz fällt viel schneller als die Sekunde (numerische Verhältnisse wurden
ignoriert). Gebunden zusammen, das Drei Einheitgewichtobjekt soll SCHNELLER als das Zwei
Einheitgewichtobjekt, aber -- gleichzeitig fallen -- LANGSAMER, da das Eineinheitgewichtobjekt
zurück das Zwei Einheitgewichtobjekt halten soll. Aber solche Argumente wurden ignoriert. verstehend die Arbeit
von Thales, Pythagoras, Eudoxus, und anderen. (Nur Die Bibel ist in mehr Kopien als
Die Elemente erschienen). Fachleute schreiben der Arbeit die ersten vier Bücher von
Pythagoras zu. Und der Buch Fünf Enthalten die große Arbeit von Eudoxus auf Verhältnissen
(SCHRIFTART).
verstehend die Arbeit
von Thales, Pythagoras, Eudoxus, und anderen. (Nur Die Bibel ist in mehr Kopien als
Die Elemente erschienen). Fachleute schreiben der Arbeit die ersten vier Bücher von
Pythagoras zu. Und der Buch Fünf Enthalten die große Arbeit von Eudoxus auf Verhältnissen
(SCHRIFTART).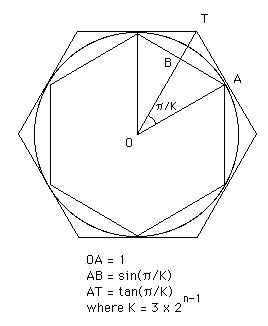 Zirka
220B.C., Archimedes hat raffiniert die Eudoxian Methode der Erschöpfung, dem Gebiet von einem
Kreis, eine frühe Schätzung von
Zirka
220B.C., Archimedes hat raffiniert die Eudoxian Methode der Erschöpfung, dem Gebiet von einem
Kreis, eine frühe Schätzung von  (Verhältnis von circumerence zu
Durchmesser von einem Kreis) -- einem weiterer Schritt nach "dem wesentlichen Nierenstein"
anzunähern, beanspruchend Pythagoräischen Geometrischarithmetik.
(Verhältnis von circumerence zu
Durchmesser von einem Kreis) -- einem weiterer Schritt nach "dem wesentlichen Nierenstein"
anzunähern, beanspruchend Pythagoräischen Geometrischarithmetik. an, der größte Frauenmathematiker alter Zeiten. Ein
paar Tage später, diese Mob haben die Bibliothek von Alexandria (die größte alte Quelle von
Mathematik und Wissenschaftenschreiben) verbrannt -- zerstörend alle Arbeiten von Eudoxus und
fast alle von jenen von Archimedes, sowie die Arbeiten von so vielen anderen Schöpfern
(SCHRIFTART).
an, der größte Frauenmathematiker alter Zeiten. Ein
paar Tage später, diese Mob haben die Bibliothek von Alexandria (die größte alte Quelle von
Mathematik und Wissenschaftenschreiben) verbrannt -- zerstörend alle Arbeiten von Eudoxus und
fast alle von jenen von Archimedes, sowie die Arbeiten von so vielen anderen Schöpfern
(SCHRIFTART).In 527 B. C. Justinian, römischer Kaiser vom Westlichen
Flügel vom römischen Reich, ist auch Kaiser vom Osten geworden. Er hat entschieden, daß der
Heide die der der Akademie wird gegründet im Namen von Platon und ander philsophical bedrohten
orthodoxes Christentum so in 529 einschult, wurden alle diese Schulen geschlossen, effektiv End
spekulative Forschung in Europa. Die Herausforderung wurde von Islamischen Gelehrten, die nicht
nur haben bewahrt die Kenntnis von den alten aber fortgeschritten ist, es in "verbotenen
Gebieten" eingenommen.
 dessen Name hat den Etikettalgorithmus für eine
gewisse Methode für Problemlösung begeistert. Und der Titel von seinem Buch auf Arithmetik hat
unser Wort für Algebra begeistert. (Beweis ist kürzlich aufgetaucht, daß vorrenaissance
islamisch -- und vielleicht jüdisch -- Gelehrte Entdeckungen gemacht haben, die später zu
europäischen Gelehrten in der Renaissance Periode zugeschrieben worden sind).
dessen Name hat den Etikettalgorithmus für eine
gewisse Methode für Problemlösung begeistert. Und der Titel von seinem Buch auf Arithmetik hat
unser Wort für Algebra begeistert. (Beweis ist kürzlich aufgetaucht, daß vorrenaissance
islamisch -- und vielleicht jüdisch -- Gelehrte Entdeckungen gemacht haben, die später zu
europäischen Gelehrten in der Renaissance Periode zugeschrieben worden sind). In 1202 "Fibonacci" (Leonardo von Pisa) hat
herausgegeben Lib Rechenbretter ("Buch vom Rechenbrett"), die ersten Europäerbücher zu benutzen
Dezimalaufzeichnung in Arithmetik (welcher Fibonacci wird gelernt in seinem eingeborenen
Nördlich Afrika). Die Ausbreitung Dezimalarithmetik hat möglich das große gemacht "Alter der
Navigation" und "Alter des Handels", der gefolgt hat -- obwohl Historiker wählen, dies zu
ignorieren.
In 1202 "Fibonacci" (Leonardo von Pisa) hat
herausgegeben Lib Rechenbretter ("Buch vom Rechenbrett"), die ersten Europäerbücher zu benutzen
Dezimalaufzeichnung in Arithmetik (welcher Fibonacci wird gelernt in seinem eingeborenen
Nördlich Afrika). Die Ausbreitung Dezimalarithmetik hat möglich das große gemacht "Alter der
Navigation" und "Alter des Handels", der gefolgt hat -- obwohl Historiker wählen, dies zu
ignorieren.Diese Mechanische Industrielle Revolution ist (oben
beschrieben) schwächer mit "Dem Schwarzen Tod" (bubonic Plage) geworden, maximierend in
1348. Der Schwarze Tod wurde von den Mängeln an Katzen verursacht, die Rattenbevölkerung zu
kontrollieren. Für Jahrhunderte hatten abergläubische Leute Katzen getötet, die sie behaupten,
die vertrauten von Hexen zu sein. (Katzenaugen
![]() können fangen irgendein Licht in einem dunklen Zimmer oder Höhle, aufleuchten wenn sonst nichts
macht. Auch in kaltem climes, streicht den eine Katze statische Aufladung aufruft, und die
Funken scintillate im dunkeln). Ein Papst hat sogar, daß das Ausrotten von Katzen befürwortet.
Deshalb durch die Mitte vom 14. Jahrhundert, hat der Mangel der Katzen erlaubt, daß die
Rattenbevölkerung zu epidemischen Verhältnissen multipliziert. Die Ratten
können fangen irgendein Licht in einem dunklen Zimmer oder Höhle, aufleuchten wenn sonst nichts
macht. Auch in kaltem climes, streicht den eine Katze statische Aufladung aufruft, und die
Funken scintillate im dunkeln). Ein Papst hat sogar, daß das Ausrotten von Katzen befürwortet.
Deshalb durch die Mitte vom 14. Jahrhundert, hat der Mangel der Katzen erlaubt, daß die
Rattenbevölkerung zu epidemischen Verhältnissen multipliziert. Die Ratten
![]() haben Flöhe getragen. Und die Flöhe haben die Plage
getragen. In 5 Jahren hat die Plage 25 Millionen, 1/3 der Bevölkerung Europas getötet. In einigen Gebieten 50% von der Bevölkerung ist in "Dem Schwarzen Tod" gestorben. Viele Gebiete haben Schmiede, Böttcher, Räderrechte, andere
Handwerker gemangelt.
haben Flöhe getragen. Und die Flöhe haben die Plage
getragen. In 5 Jahren hat die Plage 25 Millionen, 1/3 der Bevölkerung Europas getötet. In einigen Gebieten 50% von der Bevölkerung ist in "Dem Schwarzen Tod" gestorben. Viele Gebiete haben Schmiede, Böttcher, Räderrechte, andere
Handwerker gemangelt.