Given G as ground set, structurable as a distributive lattice,
D, with P as its complemented sublattice
, define infix binary operators for elements p, q
in the ground set: (1) SJ (subjuncture), 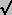 , s.t. p
, s.t. p 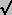 q
q  sup {x| p
sup {x| p
 q = p
q = p  x}; (2) JS (suprajuncture), p
x}; (2) JS (suprajuncture), p 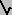 q
q  inf {x|p
inf {x|p  q = p
q = p  x}; (3) SR (subrupture,
x}; (3) SR (subrupture,
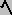 , s.t. p
, s.t. p 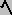 q
q  sup {x| p
sup {x| p  q =
q =  x}; (4) RS (suprarupture),
x}; (4) RS (suprarupture), 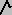 , s.t. p
, s.t. p
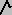 q
q  sup {x| p
sup {x| p
 q = p
q = p  x}. These 4 operators can be defined on a
partially ordered set or parorder (PL). Their combinations can only be defined on a
complemented distributive lattive or distributive lattice. Definition (5): juncture
("conditional or 'implication'"):
x}. These 4 operators can be defined on a
partially ordered set or parorder (PL). Their combinations can only be defined on a
complemented distributive lattive or distributive lattice. Definition (5): juncture
("conditional or 'implication'"): 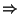

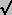

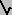 ; (6)
rupture ("subtraction"): \
; (6)
rupture ("subtraction"): \ 
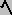

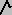 ; (7) O
; (7) O  {
{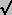 ,
,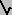 ,
, 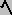 ,
,
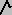 . (The conditional can be defined via
complementation, ¬: p
. (The conditional can be defined via
complementation, ¬: p 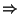 q
q  p
p  ¬p, hence, requires the ground of a complemented
lattice; similarly for its inverse, subtraction. Motivation, but not terminology for the
above is to be found in Curry17.) Definition (8), operators on O
: d is dual iff interchanging
sup, inf,
¬p, hence, requires the ground of a complemented
lattice; similarly for its inverse, subtraction. Motivation, but not terminology for the
above is to be found in Curry17.) Definition (8), operators on O
: d is dual iff interchanging
sup, inf, 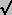 ,
, 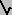 ;
t is transposition iff transposing operational tables )interchanging rows
and columns); v is inverse iff v
;
t is transposition iff transposing operational tables )interchanging rows
and columns); v is inverse iff v  dt = td. Theorem 1: dd = tt= vv = i (identity). K
dt = td. Theorem 1: dd = tt= vv = i (identity). K  {d, t, v, i} satisfies a commutative diagram,
{d, t, v, i} satisfies a commutative diagram,
SJ<--d--->JS
^ \ /^
| v\ / |
t| \ |t
| / \ |
| /v \|
V V
SR<--d--->RS
i.e., has the structure of an Abelian group on two generators (d, t
), i.e., the Klein Vieregruppe with the Cayley Table (PL):
|d t v i
d|i v t d
t|v i d t
v|t d i v
i|d t v i
Theorem 2: We have a SUBRUPTURE ALGEBRA: SR  {G,
{G, 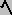 }; a SUPRARUPTURE ALGEBRA, RS
}; a SUPRARUPTURE ALGEBRA, RS  {G,
{G, 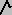 }; a SUBJUNCTURE ALGEBRA, SJ
}; a SUBJUNCTURE ALGEBRA, SJ  {G,
{G, 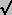 }; a SUPRAJUNCTURE
ALGEBRA, JS
}; a SUPRAJUNCTURE
ALGEBRA, JS  {G,
{G, 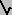 }
. Theorem 3: A
}
. Theorem 3: A  {SR, RS. SJ, JS}
is invariant under transformation of an automorphic group on G2
, namely, K.--Note: The above commutative diagram is
equivalent to the Medieval square of opposition which began with Aristotle's
syllogistic logic in the 4th century BC, containing three claims: that the syllogistic
case of A (all cases) and O (no case) [below] are contradictories, that E (some cases
exist) and I (some cases do not exist) are contradictories, and that A and E are contraries.
(The diagram has appeared in logic texts since that time. Criticized very much in recent decades,
it still finds reference.) The square of opposition embodies a group of theses in
its diagram -- theses independent of the diagram. The theses specify logical relations for
four logical forms:
{SR, RS. SJ, JS}
is invariant under transformation of an automorphic group on G2
, namely, K.--Note: The above commutative diagram is
equivalent to the Medieval square of opposition which began with Aristotle's
syllogistic logic in the 4th century BC, containing three claims: that the syllogistic
case of A (all cases) and O (no case) [below] are contradictories, that E (some cases
exist) and I (some cases do not exist) are contradictories, and that A and E are contraries.
(The diagram has appeared in logic texts since that time. Criticized very much in recent decades,
it still finds reference.) The square of opposition embodies a group of theses in
its diagram -- theses independent of the diagram. The theses specify logical relations for
four logical forms:
|
|
|
|
NAME |
FORM |
TITLE |
|
|
|
|
|
A |
Every S is P |
Universal Affirmative |
|
|
|
|
|
E |
No S is P |
Universal Negative |
|
|
|
|
|
I |
Some S is P |
Particular Affirmative |
|
|
|
|
|
O |
Some S is not P |
Particular Negative |
The diagram for the traditional square of opposition is:
 . Problem: Can this be
generalized to a group-theoretic relation between symtactic and semantic structures? between
mathematics and metamathematics? between logic and metalogic?.
. Problem: Can this be
generalized to a group-theoretic relation between symtactic and semantic structures? between
mathematics and metamathematics? between logic and metalogic?.
 , with H the Hamiltonian
function, define
, with H the Hamiltonian
function, define 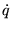 =
DpH,
=
DpH, 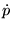 = - DqH.
Another formulation is p = D
= - DqH.
Another formulation is p = D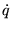 L, for Lagrangian L.
L, for Lagrangian L. , with H
the Hamiltonian function, define
, with H
the Hamiltonian function, define 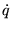 = DpH,
= DpH, 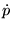 = - DqH. Then formulate
= - DqH. Then formulate 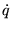 i = (qi+1 - qi)/Dt, where
qi = q(t), qi+1 = q(t + Dt
t). Then the equations of motion become qi+1 =
qi + piDt, pi+1 = pi -
Dt(DqiV)q=qi. The
latter equations are not area-preserving (PL), but can be made so, transforming a H. m.
into an area-preserving map.
i = (qi+1 - qi)/Dt, where
qi = q(t), qi+1 = q(t + Dt
t). Then the equations of motion become qi+1 =
qi + piDt, pi+1 = pi -
Dt(DqiV)q=qi. The
latter equations are not area-preserving (PL), but can be made so, transforming a H. m.
into an area-preserving map. T, log U
T, log U  W, with another constant:
T + W = CONSTANT, where T is kinetic energy
and W is "the work function" (The Variational Principles of Mechanics, Cornelius
Lanczos, p. 29). But the work fucyiom is negative potential energy (ibid.). Result:
T - V = CONSTANT, Hamilton's Principle, derived from the Antitonic
Principle. PL Lagrange's Principle derived from the Antitonic Principle (PL) , and
d'Alembert's Principle derived from Newton's Law , with antitonic form.
W, with another constant:
T + W = CONSTANT, where T is kinetic energy
and W is "the work function" (The Variational Principles of Mechanics, Cornelius
Lanczos, p. 29). But the work fucyiom is negative potential energy (ibid.). Result:
T - V = CONSTANT, Hamilton's Principle, derived from the Antitonic
Principle. PL Lagrange's Principle derived from the Antitonic Principle (PL) , and
d'Alembert's Principle derived from Newton's Law , with antitonic form. Ce
[(- w)z-1e-w]/(1 - e-w)dw,
T[z] < 0, |arg(- w)] < p, e
Ce
[(- w)z-1e-w]/(1 - e-w)dw,
T[z] < 0, |arg(- w)] < p, e  2
pk > 0, and Ce
is a Hankel contour. The Riemann zeta function (PL) can be expressed
in terms of this integral.
2
pk > 0, and Ce
is a Hankel contour. The Riemann zeta function (PL) can be expressed
in terms of this integral. 1/k. Shown to diverge (PL) (slowly) by integral test (PL) in
comparison to function 1/x. Its generalization is the
Riemann zeta function: z(n) = S
k=1
1/k. Shown to diverge (PL) (slowly) by integral test (PL) in
comparison to function 1/x. Its generalization is the
Riemann zeta function: z(n) = S
k=1 1/kn. However, the
alternating series (PL) converges: S
k=1
1/kn. However, the
alternating series (PL) converges: S
k=1 (-1)(k - 1)/k = ln 2. The
sum of the first few terms of the h. s. is given by the nth
harmonic number (PL): Hn = Sj =
1n1/j = g + y0(n +
1), where g is the Euler-Mascheroni constant (PL) and
Y(x) = y0
is the digamma function (PL). Also PL harmonic mean.
(-1)(k - 1)/k = ln 2. The
sum of the first few terms of the h. s. is given by the nth
harmonic number (PL): Hn = Sj =
1n1/j = g + y0(n +
1), where g is the Euler-Mascheroni constant (PL) and
Y(x) = y0
is the digamma function (PL). Also PL harmonic mean. 0,
0, 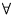 z e D. Then
z e D. Then 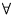 z e D, 0
z e D, 0  h(z)
h(z)  [R/(R -
|z - z0|)]2 h(z0). PL harmonic function, Harnack's
Principle, Liouville's Conformability Theorem.
[R/(R -
|z - z0|)]2 h(z0). PL harmonic function, Harnack's
Principle, Liouville's Conformability Theorem. h2
h2  ... on a connected open set (PL), H e C. Then, either hj
... on a connected open set (PL), H e C. Then, either hj 
 uniformly on compact
sets (PL), or there exists a finite-valued harmonic function h e H s. t. hj
uniformly on compact
sets (PL), or there exists a finite-valued harmonic function h e H s. t. hj  h
uniformly on compact sets.
h
uniformly on compact sets. ½vers(x) = ½(1 - cos x) = sin2
(½x).
½vers(x) = ½(1 - cos x) = sin2
(½x).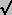 , s.t. p
, s.t. p  q = p
q = p 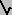 q
q  q = p
q = p 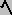 , s.t. p
, s.t. p 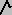 , s.t. p
, s.t. p
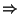
 . Problem: Can this be
generalized to a group-theoretic relation between symtactic and semantic structures? between
mathematics and metamathematics? between logic and metalogic?.
. Problem: Can this be
generalized to a group-theoretic relation between symtactic and semantic structures? between
mathematics and metamathematics? between logic and metalogic?. O
O used in
the second derivative test (PL): D
used in
the second derivative test (PL): D  -1 is the
2-D rotation operator and sought a 3-D operator, but ended with a 4-D operator:
the quaternion. However, using the multivector outer product,
-1 is the
2-D rotation operator and sought a 3-D operator, but ended with a 4-D operator:
the quaternion. However, using the multivector outer product,