Sabemos que cualquier número racional puede ser representado como un número decimal. Ejemplo: 1/3 = 0.|3|, donde |n| significa que n es repetido infinitamente, es decir con una periodicidad que comienza en algún punto en el numero decimal.
También sabemos que cualquier tal "decimal periódico" puede ser representado como una suma
geométrica de longitud infinita. Así, 1/3 
0.33333....
3/10 + 3/100 + 3/1000 + ... + 3/10n + ....
También sabemos que tales sumas de infinte son "iguales en el límite al número que es el forma racional".
Pregunta: ¿existen otras sumas infinitas no periódicas? De ser así, podemos usar estos para llenar los huecos para los valores de logaritmos que no son racionales, dando lobarithm total.
El problema no puede ser solucionado finitarily -- cuando la diferencia y el cociente prblems han sido solucionado. Debemos solucionar el logaritmo (inverso exponencial) problema transfinitarily por un nuevo operaton: LÍMITE.
(Digo "transfinitarily" desde medios "infinitos" "cerniéndome cerca allí", mientras que "transfinite" los medios "utilización del infinito causan la obra finita o infintary".)
Podemos usar estos resultados para crear "vectores infinitos" como representaciones de logaritmos-- el alcanzamiento de nuestro inverso deseado.
La definición de falta del límite es de 
Augustin Cauchy (1789-1857), "con epsilons y deltas", que deja perplejo o asusta a muchos estudiantes.
Declararé este defintion clásico. Por suerte, las matemáticas modernas proporcionan un mejor
definiton, que mostraré pronto. (También, mi gráfico para EL LÍMITE es como peatón como escalera trepadora, o descubrimiento de un calcetín
en un cajón.)
Deje Sn = s1 , s2, s 3, ..., denotan una secuencia - como en, 0.3, 0.33, 0.333, 0.3333... , o 3/10, 33/100, 333/1000, 3333/10000...., la secuencia que representa 1/3 racional .
DEFINICION: El verdadero número L es el límite de secuencia Sn si, y sólo si, para cada e > 0 allí existe a d > 0 tal esto |sn - L| < e si n > d.
El sentido de este: Designe cualquier neighborhoos del límite L (de la forma |sn - L|) y puedo especificar un positivo d (indexación a un elemento en secuencia Sn) tal que cada elemento más allá de aquella posición n reside en esto vecindad |sn - L|.
LIMITE enables Achilles para alcanzar a la Tortuga (en la PARADOJA DEL ZENO), hasta aunque Tortuga tenga delante principio de UNA UNIDAD. Aquiles puede controlar MITAD DE ESTE UNIDAD; MITAD DE LA MITAD; MITAD DE LA MITAD DE LA MITAD; indefinidamente . Es decir, 1/2, 1/2 + 1/4, 1/2 + 1/4 + 1/8, ....
Podemos obtener sumas parciales de esta secuencia: 1/2, 3/4, 7/8, ..., (2n — 1)/2n = 1 — 1/2n, .....
Pero Zeno sabía que usted no puede SUMAR ESTE POR UNA OPERACIÓN FINITARIO, de ahí, ARGUMENTADO QUE ARITMÉTICA NO PUEDE EXPLICAR MOVIMIENTO - retraso EL MECÁNICO REVOLUCIÓN INDUSTRIAL Y ESCLAVITUD DE PROLONGACIÓN HACIA 2000 años!
Podemos mostrar que el LÍMITE de esta secuencia es L = 1 . ¿Desea usted "la milliona VECINDAD"? Es decir, |sn - L| < e = 1/1000000. Bien, para n = 20, s20 = 1 — 1/1048576, y |1 - 1/1048576 — 1| = 1/1048576| < 1/1000000. Asi, lim(n->¥) (1 — 1/rn) = 1 — 0 = 1. ¡AQUILES ALCANZA A LA TORTUGA!
La definición de epsilon-delta puede ser repetida por el uso del métrico concepto , una extensión del "Teorema de Pythagorean familiar".
DEFINICIÓN: Un métrico es una no negativa funcione g(x, y) descripción "de la Distancia" (diferencia entre coordenada valores ) entre puntos vecinos para un Juego dado. Un métrico satisface la Desigualdad de Triángulo, g(x,y) + g(y,z) ³ g(x,z), y es simétrico: g(x,y) = g(y,x).
Podemos definir ahora una teoría general de secuencias , que incluirá todos aquellos para NÚMEROS RACIONALES, con subsecuencias que REPITEN, así como SECUENCIAS CONVERGENTES sin REPETIDORES para REPRESENTAR CUALQUIER VERDADERO NÚMERO.
DEFINICIÓN:Un Cauchy secuencia, {a1, a2, a
3, ...}, es una secuencia tal que su métrico, d(am
, sn) satisface limmin(m, n)
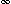d(am, an) = 0.
(Un Cauchy secuencia CONVERGE no necesariamente para todo RATIONALS, pero va a CONVERJAS para todos los VERDADEROS NÚMEROS.)
Sin embargo, antes de ver como LÍMITE hace TOTAL EL INVERSO LOGARÍTMICO de EXPONENTIATION vía VERDADERO Los NÚMEROS, vaya a estudiar "periódico y no periódico el decimal numera", en la preparación para verdaderos números (incluso irrationales).
Colindando, a las OPERACIONES FINITARY (adición, substracción, multiplicación, etc.) LA OPERACIÓN TRANSFINITARY DE LÍMITE, EL INVERSO LOGARÍTMICO de EXPONENTIATION PUEDE SER HECHA TOTAL, cuando vemos volviendo a su modelando.