More general than GEOMETRY,
TOPOLOGY is simply the study of CONNECTIONS (while geometry is the study of CONNECTED systems
with specific SHAPE and SIZE). TOPOLOGY IS NECESSARY FOR GEOMETRY, BUT
GEOMETRY IS NOT NECESSARY FOR TOPOLOGY. Infants and small children daily grapple with topology. A simple trick illustrates topology.
A man can remove his vest without taking off his coat, because (topologically)
the vest is outside the coat in the same sense that a paper in a waste basket
is outside the basket. How do it? Put arm through, say left sleeve of vest;
pull the coat through this vest-hole, leaving the vest hanging on the right arm;
then pull the vest out the right sleeve. A triangle, a square, a circle, a
rectangle are all equivalent in topology! Because each figure is
connected within the plane in the same way. Each figure separates
the plane into one inside region and one outside region. Topologists
have a special name for any figure separating the plane into one inside
and one outside region: A JORDAN CURVE (named for the French mathematician,
Camille Jordan (1838-1922), who first gave an enlightening discussion of this
subject). However, the figure-eight topologically differs from the square,
circle, or rectangle. The figure-eight is not a Jordan curve because
the figure-eight connects differently within the plane by comparison to the
Jordan curve. The figure-eight separates the plane into TWO distinct
INSIDE regions and one outside region. However, a single cut on the
figure-eight transforms it into an equivalent of the Jordan curve.
Transforming a figure by a cut provides us a classifier for plane
figures, just as plants or animals can be biologically classified as of
this genus (generative pattern). We define the Jordan curve (triangle,
circle, rectangle, etc.) as of genus zero because the Jordan curve is
the simplest of figures -- connects most simply in the plane. A triangle
requires zero cuts to transform it into the simplest form; similarly,
the square, etc. Since a single cut transforms a figure-eight into a Jordan
curve (genus zero structure), the topologists says the figure-eight is
of genus one. A figure requiring two cuts to become equivalent to a
genus-zero figure is of genus two. Etc. Kids can be taught to understand
the topology of tangles they draw on paper. Two structures
are topologiclly equivalent iff each transforms into the other tearing or ripping.
Why treat the triangle, circle, square, rectangle as the same?.
An important part of topology is the mathematical theory of knots and braids,
for understanding molecular chemistry, especially for pharmaceuticals. The unravelling
of knots mirrors the solution of algebraic equations. But topology is not
taught in our schools, or tested in standardized tests. Teachers, students,
parents, citizens alike are ignorant of its presence in our daily lives and the great
promise of its resources if we use them. Topology has been called "rubber-sheet geometry",
since any figure drawn on a rubber sheet and stretched is topologically unchanged.
Using putty or playdough, kids could experiment with topological structures -- if only
teachers knew enough or cared enough to encourage them to do so. Topology is the creation
of the great Swiss mathematician, Leonhard Euler (1707-83). PL topology, set-theoretic;
topology, general; topology, algebraic; topology, differential. "The
difference between algebraic topology, differential topology, general topology, etc. is the
measure we choose for the manifold.
The widespread ignoring of topophysics may explain the famous 20th century
Bohr-Einstein debates about quantum theory in which Einstein argued in terms of "hidden
variables" in matter, whereas Bohr argued for a contextual effect, comparable to
mechanical motion in an inertial field or electric charge in a moving system.
The combinatorial concept of cartesian product allows decomposition of topological
structure. Thus, a cylinder is the cartesian product of the circle and the line
segment.
This provides for what might be called "topological primes" -- comparable to prime numbers
in arithmetic wich form composite numbers. Thus, every mathematical structure may be
considered as formed of the basic components:
- vertex;
- edge;
- face;
- hole;
- cross-cap.
In the file, "Topology in Thermodynamics", at this Website, I described how Gibbs
derived his famous phase-rule from Euler's polygonal rule, involving the first three of the above topological primes.
This rule is extended to the xxxx to encompass holes, and a further extension encompasses
th cross-cap, made possible by the m&oml;boid.
Student of biophysics should the basis of topology in their field. A step towards this
was made by the book, xxxxx, by xxx, which discusses this in chemical structures that also
occur in biophysics.
The definition of topology can be reduced to one sentence via the notion of the
topological transformation labeled "homeopmorphism":
- an n-ball is a "sphere" in n-
dimensional space with center, x and radius
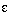 ;
;
- a neighborhood (
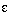 -neighborhood) of a point in a point set
is an n-ball containing the point;
-neighborhood) of a point in a point set
is an n-ball containing the point;
- an open set of a point set is one in which the neighborhood of each point is
confined to the set;
- a map from an open set in a manifold is a homeomorphism if, and only if,
the target is an open set;
- topology is the study of all properties of a space conserved by a homeomorphism.
topometrics. This is a better label
for the subject traditionally labeled "geometry" (from "measurement of earth", for surveying
fields). But a geometry is simply a topology (PL) adjoined to a metric
(PL). Most of our daily concerns are topological rather than topometric
(geometric).
An Abridged History of Topology.
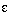 ;
;
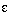 -neighborhood) of a point in a point set
is an n-ball containing the point;
-neighborhood) of a point in a point set
is an n-ball containing the point;